3. Описание экспериментальной установки

Установка представляет собой горизонтально расположенный вал 1 (рис.3), закрепленный на основании 2, на котором расположены массивный маховик 3 и два шкива различного диаметра 4. При выполнении лабораторной работы на один из шкивов наматывается нить, на которой закреплен груз 5. Для закрепления нити на шкивах предусмотрены штыри 6.

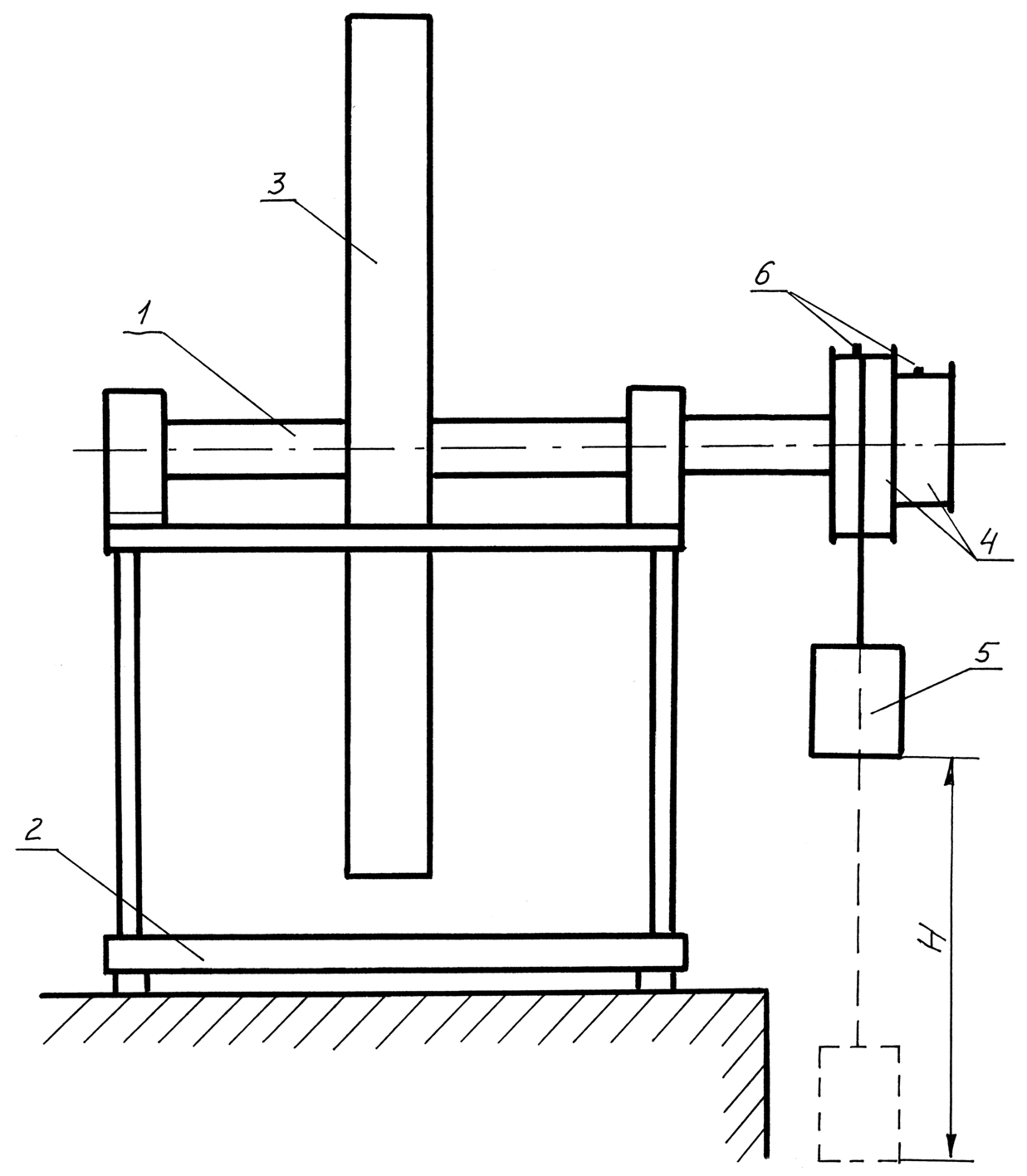
Рис. 3. Схема установки

3. Вывод расчетной формулы

Рассмотрим механическую систему, состоящую из груза массой m и маховика со шкивами и валом с моментом инерции I. В тот момент, когда груз массой m поднят над полом на высоту Н и находится в покое, полная механическая энергия системы равна потенциальной энергии груза

. (12)

Непосредственно перед падением груза на пол его потенциальная энергия равна нулю, а полная механическая энергия системы состоит из кинетической энергии поступательного движения груза и кинетической энергии вращательного движения маховика , то есть имеем

. (13)

Если считать, что на маховик действуют силы трения, момент которых относительно оси вращения остается постоянным, то, в соответствии с (11), можно записать

, (14)

где - число оборотов маховика за время падения груза.

Поскольку силы трения, действующие на маховик, можно считать постоянными, то движение груза m является равноускоренным и описывается уравнениями

, (15)

, (16)

где а – линейное ускорение груза,

υ– скорость груза перед ударом о пол,

t – время падения груза до пола

При этом

, (17)

где w – угловая скорость вращения маховика в момент удара груза о пол,

r – радиус шкива, на который намотана нить, удерживающая груз.

Из (15) - (17) следует:

, (18)

. (19)

Определим постоянную c. Для этого рассмотрим систему маховик – груз после того, как груз упал на пол и остался лежать на полу. Полная механическая энергия системы после падения груза на пол равна кинетической энергии вращательного движения маховика , и маховик продолжает вращаться с равномерно уменьшающейся угловой скоростью (равнозамедленное движение). В тот момент, когда маховик перестает вращаться, полная механическая энергия системы станет равна 0. В соответствии с (11)

, (20)

где - число оборотов маховика до полной остановки.

Отсюда

, (21)

. (22) Подставим (12), (13), (22) в (14):

. (23)

Выражая из (23) момент инерции I, получим

. (24)

Подставляя (18), (19) в (24) и учитывая, что , где d – диаметр шкива, окончательно получим

(25)