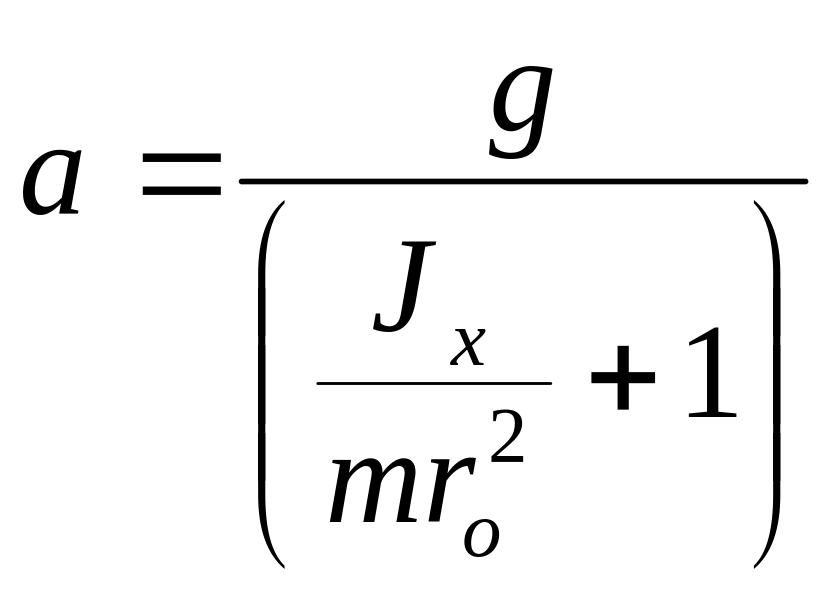6. Контрольные вопросы

1. Запишите и объясните основной закон вращательного движения твердого тела относительно неподвижной оси вращения.

2. Что такое момент силы, момент импульса, угловая скорость, угловое ускорение?

3. Как определяется момент инерции твердого тела?

4. В чем заключается теорема Штейнера? Зависит ли момент инерции от выбора оси вращения?

5. Какие законы использовались при выводе расчетных формул в данной работе?

6. Как экспериментально можно определить момент инерции крестовины маятника Обербека?

7. Почему для повышения точности эксперимента следует стараться уменьшить момент сил трения?

8. С какой целью проводится балансировка маятника (подвижные грузы укрепляются на равном растоянии от оси вращения так, чтобы маятник находился в состоянии безразличного равновесия)?

9. Как можно рассчитать абсолютную погрешность при определении углового ускорения маятника , момента силы натяжения нити М_н?

7. Библиографический список

1. Савельев И.В. Курс физики. Т.1-М.: Наука, 1989г.- 352 с., §§28-34.

2. Сивухин Д.В. Общий курс физики. Т.1-М.:Наука, 1979 г.- 420 с.

3. Каленков С.Г., Соломахо Г.И. Практикум по физике. Механика. – М.: Высшая школа, 1990г. –111 с., стр. 7-22, 40-44, 47-49.

Лабораторная работа мb2 Маятник Максвелла

1. Цель работы

Изучение вращательного движения твердого тела с помощью маятника Максвелла.

2. Теоретические основы работы

Маятник Максвелла представляет собой диск D жестко посаженный на тонкий стержень С (рис.1). На стержне по обе стороны от диска намотаны две нити Н, концы которых закреплены на горизон­тальном кронштейне К. Для изменения массы маятника на диск насаживаются сменные кольца.

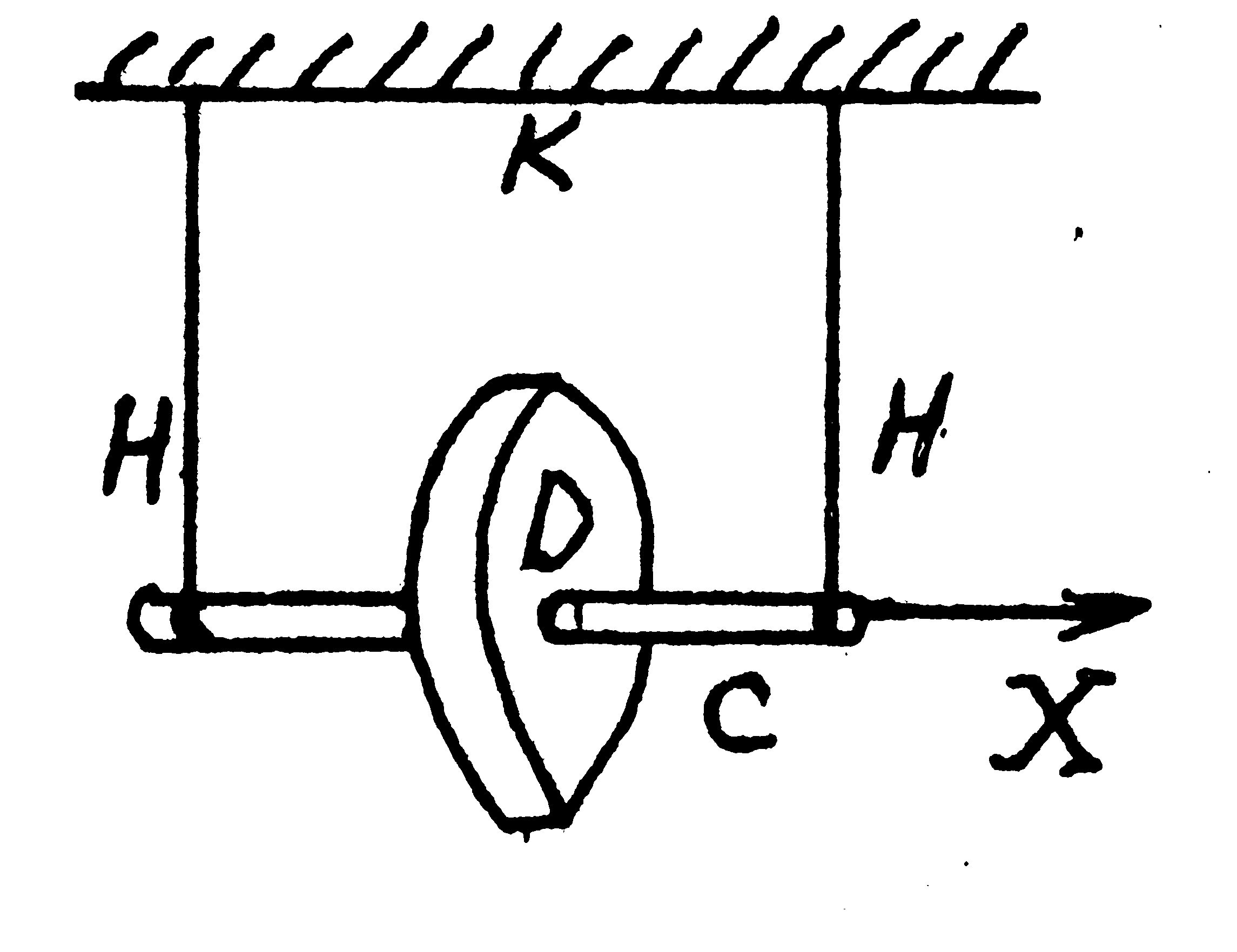
Рис.1. Маятник Максвелла

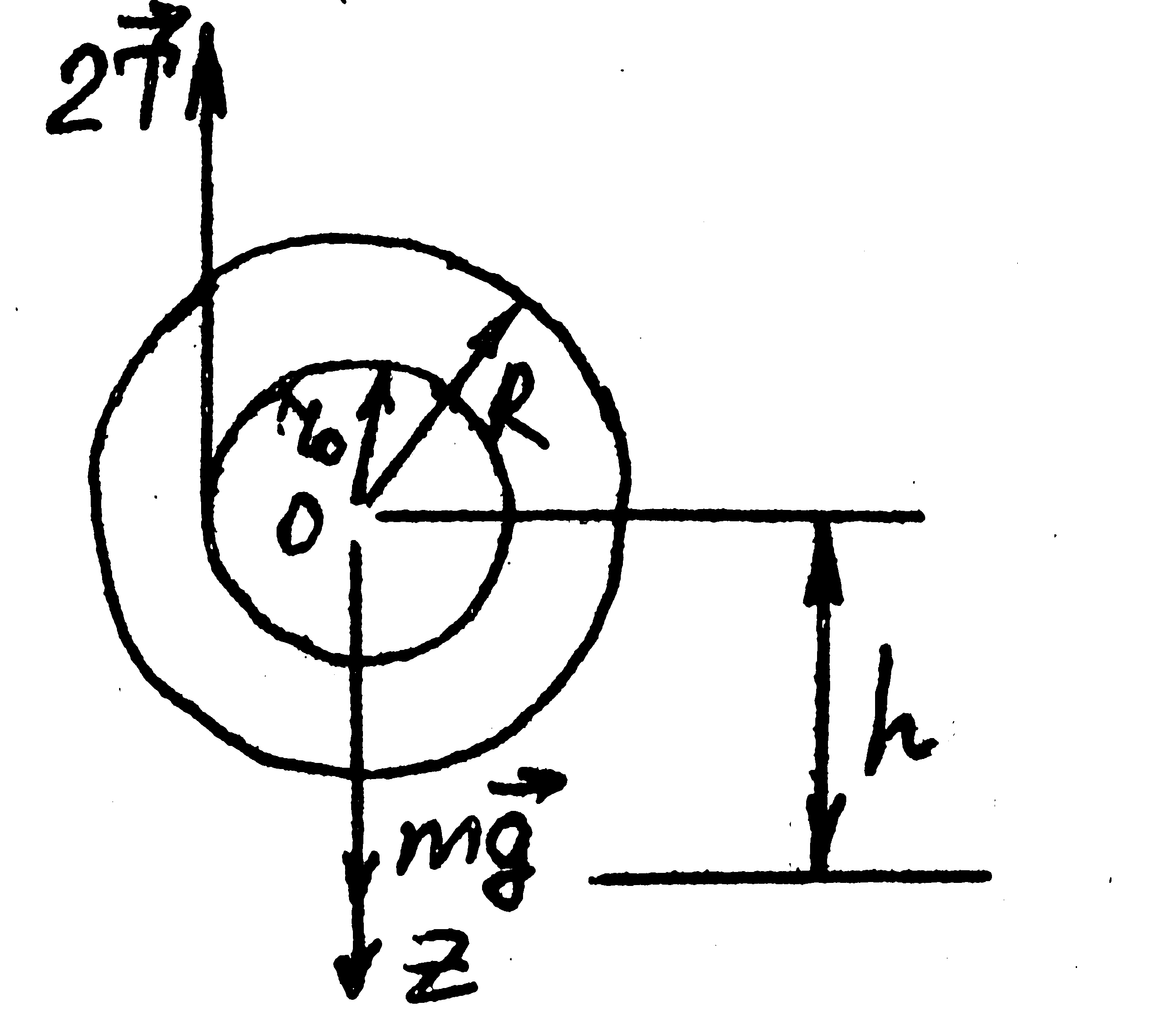
Рис.2. Параметры маятника Максвелла и силы,

Действующие на него

Если отпустить диск, то он начнет опускаться под действием силы тяжести, одновременно вращаясь. Таким образом, при плоском движении маятник участвует одновременно в двух движениях: в поступательном движении вдоль оси Z и вращательном движении относительно оси X, проходящей через его центр масс 0. Поэтому, чтобы описать движение маятника, необходимо решить систему двух уравнений: 1) уравнения, описывающего поступательное движение маятника (второй закон Ньютона), 2) уравнения, описывающего вращательное движение (основной закон динамики вращательного движения). Для написания первого уравнения рассмотрим все cилы, действующие на маятник (рис.2). Это сила тяжести , приложенная к центру масс системы 0, и сила натяжения двух нитей , приложенная к стержню в точках касания нитей.

Запишем второй закон Ньютона в проекции на ось Z:

или в нашем случае:

(1)

где - линейное ускорение центра масс маятника, m – масса маятника, равная сумме масс стержня, диска и сменного кольца (массой нитей пренебрегаем):

Для написания основного закона динамики вращательного движения определим моменты сил, действующих на маятник относительно оси вращения X. Момент силы тяжести относительно этой оси равен нулю, так как сила тяжести приложена к центру масс маятника, через который проходит ось вращения. Момент сил натяжения нитей , где

- радиус стержня. Согласно основному закону динамики вращательного движения этот момент сообщает маятнику угловое ускорение e:

, (2)

где -момент инерции маятника относительно собственной оси X. Считая нить нерастяжимой, накручивающейся на стержень без проскальзывания, можно написать связь линейного ускорения с угловым:

(3)

Получаем систему уравнений:

Решим ее относительно .

Из (2) и (3):

(4)

Из (1):

Подставим в (4):

Разделим обе части этого равенства на :

Откуда

(5)

Соотношение (5) показывает, что ускорение - величина постоянная, так как величины , и являются постоянными для маятника с данным сменным кольцом.

Ускорение маятника Максвелла можно получить и другим способом с помощью закона сохранения энергии. Полная кинетическая энергия твердого тела при плоском движении равна сумме кинетической энергии поступательного движения и кинетической энергии вращательного движения вокруг оси, проходящей через его центр масс. Для нашего маятника, находящегося в определенный момент времени t на высоте z над столом, скорость поступательного движения , угловая скорость вращения  связана с линейной скоростью: , ускорение . Потенциальная энергия маятника в момент нахождения его на высоте z равна .

Таким образом, закон сохранения механической энергии в нашем случае запишется в следующем виде:

₍₆₎

Преобразуем данное равенство:

(7)

Продифференцируем (7) по времени:

или

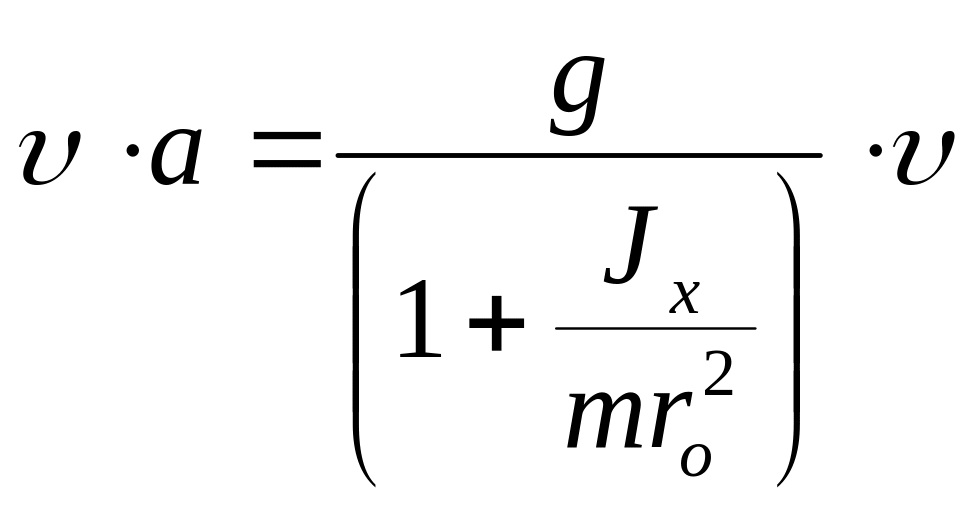
Следовательно, аналогично (5):