6.4. Прохождение широкополосного случайного процесса через частотно – избирательные цепи

Литература: [Л.1], стр. 256-257

[Л.2], стр. 450-451

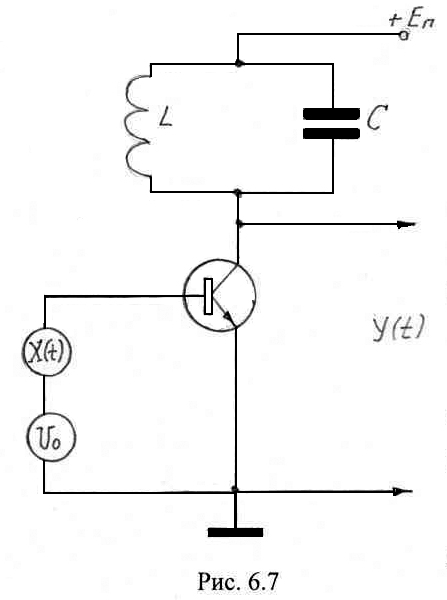Задачу преобразования широкополосного СП через частотно – избирательную цепь рассмотрим на примере одноконтурного резонансного усилителя (рис. 6.7) в режиме малого сигнала. В этом режиме, как известно, усилитель можно считать линейной частотно – избирательной цепью.

Амплитудно – частотная характеристика усилителя в режиме малого сигнала описывается выражением

, (6.22)

где , .

Переходя от относительной к абсолютной расстройке, запишем

, (6.23)

где – постоянная времени цепи.

Найдем шумовую полосу резонансного усилителя

,

или в циклических частотах

. (6.24)

Перейдем к рассмотрению статистических характеристик процесса на выходе резонансного усилителя, если на его вход поступает широкополосный СП вида «белого шума» с энергетическим спектром . В соответствии с (6.9) и с учетом того, что

,

получим выражение для энергетического спектра процесса на выходе усилителя

, (6.25)

Автокорреляционная функция находится в соответствии с теоремой Винера–Хинчина

. (6.26)

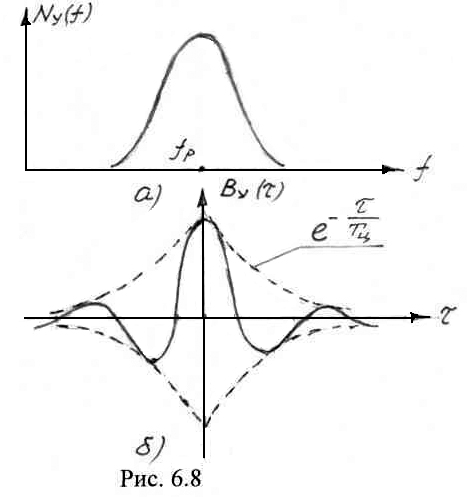
На рис. 6.8 изображены энергетический спектр и автокорреляционная функция процесса на выходе усилителя. Из рисунка следует, что АКФ выходного процесса имеет колебательный характер, уменьшаясь по закону . При этом, чем больше добротность контура, т.е. чем больше , тем медленнее спадает АКФ. Теоретически при АКФ выходного процесса преобразуется в АКФ детерминированного радиосигнала с частотой . Объясняется это тем, что при любая реализация СП на выходе представляет собой квазигармоническое колебание, частота которого в среднем равна резонансной частоте контура. И наконец, дисперсия (средняя мощность) выходного процесса

. (6.27)

6.5. Преобразование случайных сигналов нелинейными радиотехническими цепями

Литература: [Л.1], стр. 300-301

[Л.2], стр. 466-473

[Л.3], стр. 264-269

Решение задачи преобразования случайных сигналов линейными радиотехническими цепями осуществлялось спектральным методом. При этом, определялись характеристики , , при известных и комплексном коэффициенте передачи цепи . Что касается функции распределения или плотности вероятности значений выходного процесса, то задача их определения является достаточно сложной и поддается решению лишь в отдельных частных случаях.

При решении задачи преобразования случайного процесса нелинейными цепями, наоборот, плотность вероятности определяется сравнительно просто, а определение и сопряжено со значительными трудностями. Поэтому, постановка задачи преобразования СП нелинейными цепями отличается от постановки задачи преобразования СП линейными инерционными цепями.

Напомним, что основной характеристикой нелинейного безынерционного элемента является вольт – амперная характеристика

, (6.28)

где – входной сигнал,

– выходной сигнал нелинейного элемента.

Отметим, что входной и выходной сигналы связаны детерминированной функциональной зависимостью .

Так как в рассмотренном случае входной и выходной сигналы являются случайными процессами, т.е.

, ,

то выражение (6.28) можно записать так

. (6.29)

Сформулируем теперь задачу. На вход безынерционного нелинейного элемента, описываемого характеристикой (6.29) поступает стационарный случайный процесс с известной плотностью вероятности (рис. 6.9). Необходимо определить плотность распределения вероятности выходного процесса . Задачу будем решать при следующих предположениях:

– входной процесс является стационарным эргодическим процессом;

– существует и известна функция

, (6.30)

обратная функции .

Изобразим на рис. 6.10 а) зависимость и реализации входного и выходного случайных процессов.

Поскольку процесс подвергается неслучайному функциональному преобразованию этому же преобразованию подвергается и плотность вероятности . На рис. 6.10б показана характеристика и кривые плотности вероятности и входного и выходного случайных процессов.

Установим соответствие между и . Выберем некоторое значение входного процесса. Этому значению однозначно соответствует значение выходного процесса. Придадим значению элементарное приращение . Этому приращению будет соответствовать элементарное приращение выходного процесса. Так как зависимость однозначна, то вероятность того, что значение случайной величину будет находиться в пределах , должна быть равна вероятности того, что случайная величина будет находится в пределах , т.е.

. (6.31)

Но, с другой стороны

,

.

Тогда (6.31) можно представить следующим образом

, (6.32)

откуда следует

. (6.33)

Производная в (6.33) вычисляется по абсолютной величине (по модулю) в силу того, что функция может быть отрицательной, а плотность вероятности всегда положительна.

Так как по условию задачи известна функция обратная , т.е. , то (6.33) можно записать так

. (6.34)

Выражение (6.34) является основным результатом решения задачи нелинейного преобразования.

Если функция неоднозначна (имеет несколько ветвей (рис. 6.10 в)), то (6.34) принимает вид

. (6.35)

Перейдем к определению вероятностных характеристик выходного процесса. Математическое ожидание при известном определяется следующим образом

.

Но с другой стороны, учитывая (6.32), а также , получим

. (6.36)

Аналогично, для дисперсии

. (6.37)

Расчеты по этой формуле достаточно просты, если допускает степенную аппроксимацию.

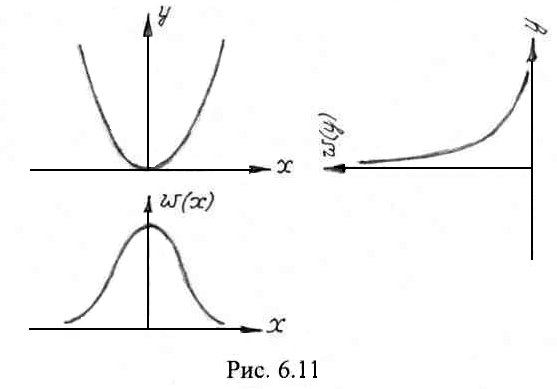
Выражение (6.34) позволяет найти при конкретном виде зависимости . Так, пусть на вход нелинейного элемента с характеристикой , поступает случайный сигнал с нормальной одномерной плотностью вероятности (рис. 6.11)

. (6.38)

Найдем функцию, обратную функции

.

Модуль первой производной

.

Далее отметим, что функция двузначна (имеет две ветви) и сигнал при любом принимает неотрицательные значения.

С учетом отмеченных обстоятельств, воспользовавшись (6.35) запишем:

Но для нормального закона (6.38)

,

Тогда окончательно получим

На рис. 6.11 изображена кривая плотности вероятности .