Таким образом или , (7)

где величина

Рис. 2

(8)

называется моментом инерции тела относительно оси Z .

Тогда уравнение динамики тела, вращающегося относительно неподвижной оси Z [см. (6)], можно записать в виде 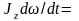M_zВНЕШН или M_zВНЕШН.

Вопрос № 29 Момент инерции тела относительно оси вращения

Момент инерции - величина, характеризующая  распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. 

Момент инерции тела относительно оси вращения  зависит от массы тела и от распределения этой массы. Чем больше масса тела и  чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:

 

.

 

Момент инерции всего тела относительно оси равен:

 

 

или, для непрерывно распределенной массы:

 

.

 Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера. Согласно теореме Штейнера момент инерции тела относительно какой-либо оси IA равен моменту инерции тела равен инерции тела относительно параллельной оси, проходящей через центр масс IC, сложенному с величиной ma2, где a - расстояние между осями: 

IA = IC + ma2.

2) Теорема Штейнера

Теорема Гюйгенса-Штейнера, или просто теорема Штейнера (названа по имени немецкого математика Якова Штейнера и голландского математика, физика и астронома Христиана Гюйгенса):

Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями.

Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции тела относительно некоторой оси.

Для краткости добавлю к своему ответу данную шпаргалку:

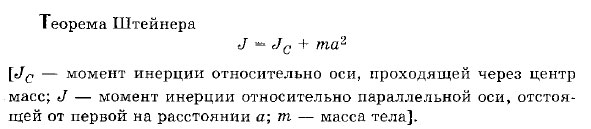
Вопрос № 30.Основное уравнение динамики вращательного движения.

Для вывода основного уравнения динамики вращательного движения используем формулу для определения работы при вращении тела

 

                                         ,                                             (7)

 

где   – момент силы относительно оси Z. Работа при вращении тела идет на увеличение его кинетической энергии

 

.

 

Продифференцируем выражение (5):

 

                                     ;                                   (8)

 

,

Учитывая, что  ,   , получаем

.

 

В векторном виде это выражение имеет вид

 

.                                                      (9)

 

Уравнение (9) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Вопрос 31 Кинетическая энергия при плоском движении абсолютно твердого тела. Кинетическая энергия вращения

Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях

кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений

.

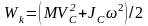если разбить плоское движение тела на поступательное со скоростью центра масс V_c и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V_c, а другое – угловой скоростью w.

при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия