Вопрос 44

Вопрос 45.Скорость, ускорение и энергия гармонических колебаний.

Колебания, при которых изменения физических величин происходят по закону синуса или косинуса, называются гармоническими колебаниями.

ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания.

Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия.

Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.

Выражение, стоящее под знаком cos или sin, называется фазой колебания

Величина - максимальная скорость колебательного движения (амплитуда колебаний скорости).

Следовательно, для скорости при гармоническом колебании имеем:

, а для случая нулевой начальной фазы

Величина - максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы

Вопрос 46 . Сложение гармонических колебаний одинакового направления и одинаковой частоты.

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

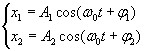(1)

Уравнение результирующего колебания будет иметь вид

(2)

Убедимся в этом, сложив уравнения системы

(3)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

(4)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

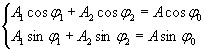(5)

Рассматривая (5) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

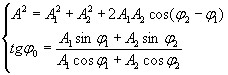(6)

Подставляя (5) в (4), получим (7)

Или окончательно, используя теорему косинусов суммы, имеем:

(8)

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

Дополнительно

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

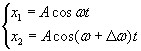(8)

Решим систему

(9)

(10)

(11)

Решение системы:

(12)

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

(13)

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω