Вопрос 39. Энергия, импульс в релятивистской механике.

Импульс релятивистской частицы

.

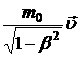Энергия   тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой 

, (77)

- скорость света в вакууме.

Энергия покоя тела

,

 - масса покоящегося тела.

Кинетическая энергия релятивистской частицы

.

Связь между энергией   и импульсом  частицы.

Вопрос 40. Основное уравнение релятивистской динамики. Закон сохранения релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

                                                                     

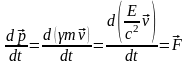
где

                                                            

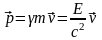
— релятивистский импульс материальной точки.

Вопрос 41.Кинетическая энергия релятивистской частицы. Закон сохранения энергии

Релятивистская частица — частица, движущаяся с релятивистской скоростью, то есть скоростью, сравнимой со скоростью света. Движение таких частиц, рассматриваемых как классические (неквантовые) материальные точки, описывается специальной теорией относительности.

Полная энергия тела (частицы) в релятивистской механике ,она складывается из энергии покоя тела 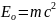и кинетической энергии 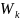, т.е. 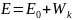, отсюда

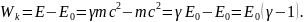
Из этого следует что при и т.е. получаем выражение кинетической энергии частицы, которое используется в ньютоновской механике.

Заметим, что энергия покоящегося тела в ньютоновской механике 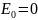а в в релятивистской 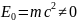. В силу однородности времени в релятивистской механике, как и в ньютоновской механике, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется.

Вопрос 42.Пространство-время как форма существования материи

Простр. и время обладают своими свойствами. Прост. обладает трехмерностью, оно симметрично, т.е. нет не обратимых процессов, пространство однородно (каждая точка пространства м.б. взята за начало координат), пространство изотропно, т.е. нет привилегированных направлений (вверх, вниз, влево, вправо). Время – длительность, оно асимметрично, т.е. необратимо. Время может пониматься по-разному: циклическое время (календари); время может толковаться как некоторая симметрия, т.к. ряд процессов не является не обратимыми; время может пониматься как стрела, т.е. время необратимо, нельзя вернуться в прошлое. Время отличается от вечности, вечность не меняется и не имеет времени, вечность это всегда настоящее.

С точки зрения теории относительности масса тела т характеризует его энергию покоя , согласно соотношению Эйнштейна:

. (17)

То есть энергия покоя тела пропорциональна его массе. Именно утверждение о том, что в инертной покоящейся материи таятся огромные (благодаря квадрату скорости света ) запасы энергии, сделанное Эйнштейном в 1905 г., является главным практическим следствием теории относительности. Основной вывод теории относительности сводится к тому, что пространство и время взаимосвязаны и образуют единую форму существования материи: пространство-время. Наиболее общая теория пространства-времени называется общей теорией относительности или теорией тяготения, т.к. согласно этой теории свойства пространства-времени в данной области определяются действующими в ней полями тяготения.

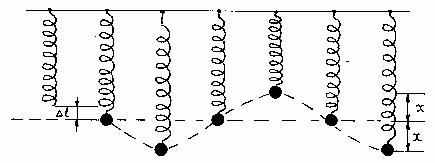
Вопрос 43.                     В качестве механической колебательной системы, на примере которой мы будем рассматривать колебания, выбираем пружинный маятник: маленькое тело (материальная точка) массой m подвешено на пружине с жесткостью k  (Рисунок 2).

Ненагруженная пружина имела длину l₀. Когда подвесили тело, пружина удлинилась на ∆l. Возникшая упругая сила уравновесила силу тяжести   .  Это соотношение позволяет определить положение равновесия пружинного маятника. Если теперь тело сместить относительно положения равновесия на расстояние х, то на тело будет действовать сила упругости и сила тяжести.

Равнодействующая этих сил равна:

 

.

 

Знак минус означает, что направление силы F_упр. и направление смещения х противоположны.  F_упр.  - сила упругости, возникающая при смещении тела относительно положения равновесия за счет сжатия или растяжения пружины (в зависимости от того, в какую сторону от положения равновесия отклонено тело). Качественно на Рисунке 1.1  виден результат действия упругой силы ( чем больше смещение, тем больше Fупр.).

 

Рисунок1.1 – Положения пружинного маятника за время одного периода колебаний.

 

Если система совершает колебания под действием сил, развивающихся в самой колебательной системе без внешних воздействий и без учета сил сопротивления, то колебания называются незатухающими собственными колебаниями. Отсутствие затухания колебаний характерно для идеальной колебательной системы, которая является физической моделью реальных физических процессов.

2. Дифференциальное уравнение, соответствующее колебаниям пружинного маятника, можно получить из закона его движения, которым является 2-й закон Ньютона  ma = F.

Учитывая, что ускорение есть вторая производная от смещения по времени  , а сила, действующая на тело, есть сила упругости, определяемая для малых смещений тела от положения равновесия по закону Гука, как   , получим

 

     или       .

 

Это дифференциальное уравнение второго порядка для незатухающих колебаний. Основной его отличительной особенностью является тот факт, что вторая производная от смещения по времени (т.е. ускорение) пропорциональна смещению. Дифференциальное уравнение, в которое величина х входит в нулевой или первой степени, называется линейным дифференциальным уравнением. В дальнейшем мы покажем, что подобного рода уравнения характерны для незатухающих колебаний в любой идеальной колебательной системе.

Перенесем все члены уравнения в левую часть и приведем дифференциальное уравнение  к виду:

 

 

Величина  , обозначим ее   , получим

 

.

 

2.                      Решением дифференциального уравнения такого вида являются функции:

 

  или   .

 

Эти решения называются уравнениями колебаний, они позволяют вычислить смещение х пружинного маятника в любой момент времени. Колебания, при которых характеризующие их физические величины изменяются по закону синуса или косинуса, называются гармоническими.

Отличие аргументов функций синуса и косинуса составляет  , т.е.  . В дальнейшем чаще всего мы будем использовать решение дифференциального уравнения в виде