4. Перспектива параллельных прямых

Относительно друг друга прямые могут быть параллельными, пересека­ющимися, скрещивающимися. Из практики перспективы известно, что па­раллельные прямые кажутся нам сходящимися в одной точке. Например, если встать на железной дороге, то увидим, что по мере удаления от нас рас­стояние между рельсами будет сокращаться, и они будут сходиться в одной точке (рис. 77). То же самое можно наблюдать на станции «Кропоткинская» Московского метрополитена (рис. 78). Линии пола и колонн сходятся в одной точке, расположенной на линии горизонта — это глубинные прямые.

Построим на проецирующем аппарате перспективу пучка параллель­ных прямых А^А^, BqB'^ и прямой Е'₀Ё_Х , лежащих в предметной плоско­сти и произвольно расположенных к картине (рис. 79). Построим перспек­тиву каждой прямой. Для этого воспользуемся имеющимися точками

47

Рис. 77 Рис. 78

(А^ = A_k ) (Bq =B_k) (E₀ = E_k), т. е. картинными следами этих прямых. Опре­делим предельную точку каждой прямой. Для всех заданных прямых она будет общая — А*,, так как определяется одним и тем же лучом зрения SA^, проведенным параллельно им до пересечения с линией горизонта.

Произвольно направленные горизонтальные параллельные прямые на кар­тине изображаются пучком прямых, сходящихся в одной предельной точке. Общая предельная точка произвольно расположенных горизонтальных па­раллельных прямых находится на линии горизонта и называется точкой схо­да (рис. 80). Заметим, что данная точка схода может лежать в любом месте на линии горизонта в зависимости от направления прямых (рис. 81).

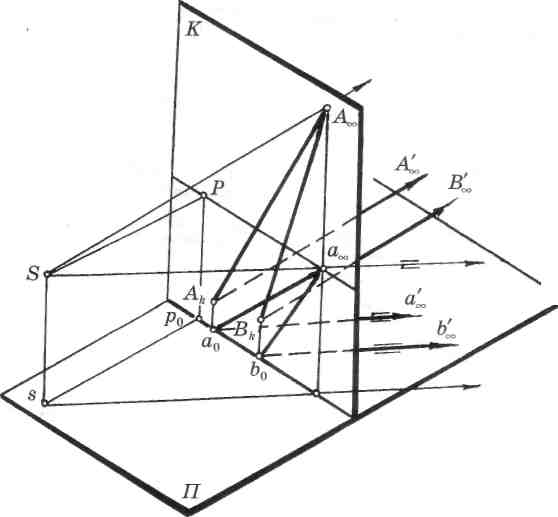
Рассмотрим построение перспективы восходящих параллельных пря­мых общего положения A_k A^, и В_кВ'„ (рис. 82). Если восходящие прямые параллельны, то их проекции на предметную плоскость а₀ а'^ и Ь₀ Ь£, также параллельны. Проекции параллельных прямых лежат в предметной плос­кости, поэтому имеют общую предельную точку а^ — точку схода на ли­нии горизонта. Точка схода А^ восходящих параллельных прямых лежит на перпендикуляре, проведенном к линии горизонта через точку схода их проекции — а^ (рис. 83).

Восходящие параллельные прямые общего положения имеют точку схода, расположенную над линией горизонта в произвольном месте и лежащую на одном перпендикуляре с точкой схода проекций этих прямых (рис. 84).

Аналогично строят изображения нисходящих параллельных прямых. Разница лишь в том, что их точка схода Б_те располагается в произвольном месте под линией горизонта (рис. 85).

48

49

Рис. 82

h _P / /		'А»
_Ро,

Рис. 83

Рис. 84

50

Рис. 86

к Признаком параллельности прямых общего положения, изображенных на картине, является расположение на одном перпендикуляре точек схода прямых и их проекций. При этом точка схода проекций параллельных пря­мых должна лежать на линии горизонта (рис. 86).

Прямые, параллельные картине, изображаются на ней параллельными.

Если параллельные прямые фронтальные, то в перспективе они оста­ются параллельными, а их проекции параллельны основанию картины, поскольку и прямые, и их проекции не имеют предельных точек, напри­мер прямые АВ и СЕ на рисунке художника А. Шибанова (рис. 87).

Если параллельные прямые вертикальные, то в перспективе они оста­ются вертикальными и параллельными между собой, так как не имеют пре­дельной точки — прямые KN и LM.

Если параллельные прямые горизонтальные (параллельные картинной и предметной плоскостям), то в перспективе они и их проекции остаются парал­лельны друг другу и основанию картины, например линии крыши TQ и OR.

Знание закономерностей изображения параллельных прямых помогает ■г передать трехмерное пространство на плоскости листа.

51

Рис. 87