3. Перспектива точки

Все без исключения перспективные изображения на плоскости карти­ны строятся в результате последовательного выполнения необходимых под­собных геометрических построений, относительная точность которых обес­печивает достаточную правильность перспективного изображения, соответ­ствующего зрительному восприятию. Значение и последовательность

23

подсобных геометрических построений рассмотрим на получении перспек­тивного изображения точки методом центрального проецирования.

Точка является основным геометрическим элементом любого объекта, перспектива которого подлежит построению ил и проверке. Перспектива вся­кого отрезка прямой, ограниченного в своих линейных размерах конечными точками, всегда может быть построена по перспективам двух точек. Перспек­тива всякой плоскости, расположенной в предметном пространстве, строит­ся по перспективам трех точек, лежащих в рассматриваемой плоскости и не находящихся на одной прямой. Перспектива поверхности, расположенной в предметном пространстве, строится по перспективам точек.

Метод построения рисунка с натуры и по представлению « по точкам » был принят и применен в преподавании П.П. Чистяковым. Позднее этот метод, существенно обогащенный педагогическим опытом, успешно применялся его преемником и последователем по академической школе В.Е. Савинским, который справедливо считал метод построения изображений «по точкам» принципом академического рисунка.

Положение всякой точки в пространстве может быть определено коор­динатами X, Y и Z (рис. 26). За начало координат примем точку р₀ — осно-

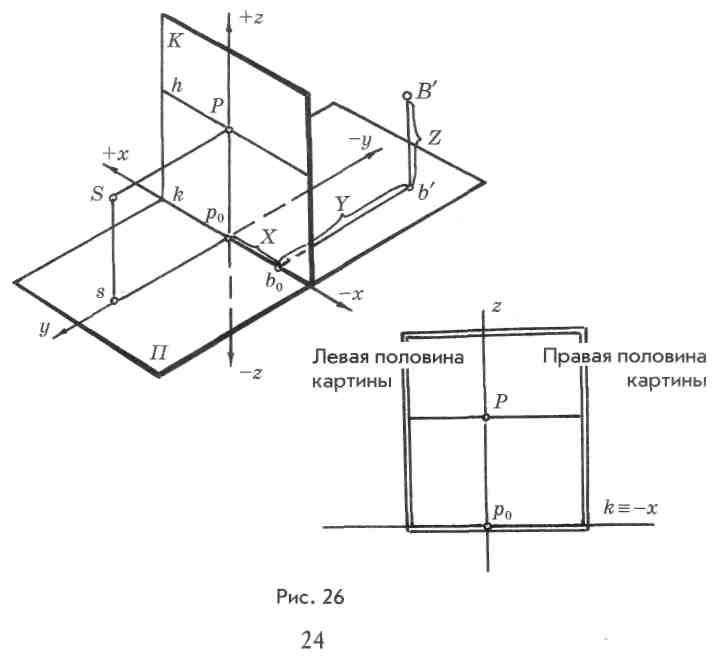
вание главного вертикала. Ось X совпадает с основанием картины к, ось Z — с главным вертикалом картинной плоскости, ось Y перпендикулярна плоскости картины.

Лампочка электрического фонаря на улице (рис. 27) представляет в на­туре точку А', ее проекция — точка а'.

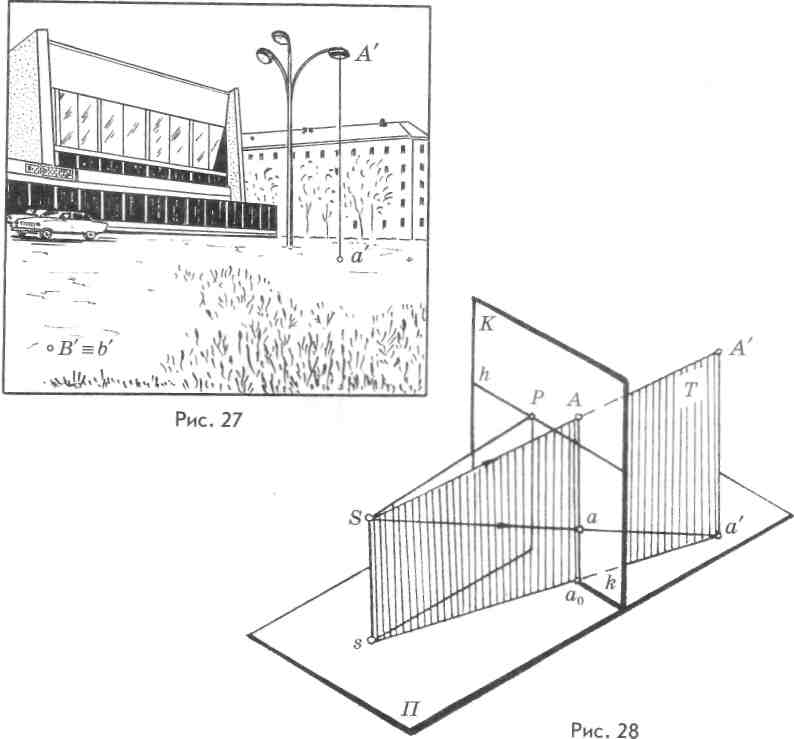
Рассмотрим расположение точки А', в системе проецирующего аппа­рата. В предметной плоскости зададим точку и ее основание (рис. 28). Че­рез высоту точки зрения Ss и проецирующий луч SA' проведем вспомога­тельную плоскость Т.

Необходимыми геометрическими элементами при построении перспек­тивы точки А' будут:

25

— sa — линия пересечения вспомогательной плоскости Т с предмет­ной плоскостью П. Эта линия, пересекая основание картины k, отмечает

на нем точку а₀, связывая тем самым заданный объект А' и точку зрения S через проекции а' и s с основанием картины.

—Аа₀ — линия пересечения плоскости Т с картинной плоскостью. Опре­деляет прямую, на которой должна лежать перспектива точки А' — точка А

Определим местонахождение перспективы А на линии Аа₀. Для этого проведем в плоскости Г луч зрения S А'. Он пересечет линию Аа₀ и отметит на ней точку А, которая и является перспективой точки А'.

На картине (рис. 29) видно, что перспектива точки А и ее основание а расположились на одном перпендикуляре к линии горизонта и основанию картины.

Положение точки называется общим, если она расположена в предмет­ном пространстве и находится на некотором расстоянии от предметной и картинной плоскостей. Точка А' является точкой общего положения.

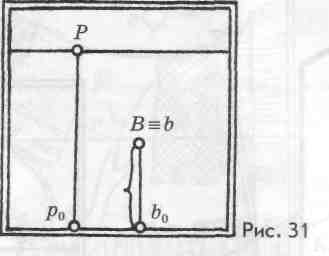
Рассмотрим случай, когда пространственная точка В'лежит на земле (рис. 2 7). В проецирующем аппарате она располагается на предметной плос­кости П. Ее основание совпадает с самой точкой В' = Ъ' и расстояние до пред­метной плоскости равно 0 (рис. 30). Перспективу точки В'и ее основания Ъ' построим аналогичным способом. Перспектива точки В и ее основание Ъ на картине лежат на одном перпендикуляре и совпадают (В з Ъ) (рис. 31). Точка В находится ниже линии горизонта, справа от главного вертикала Рр₀.

26

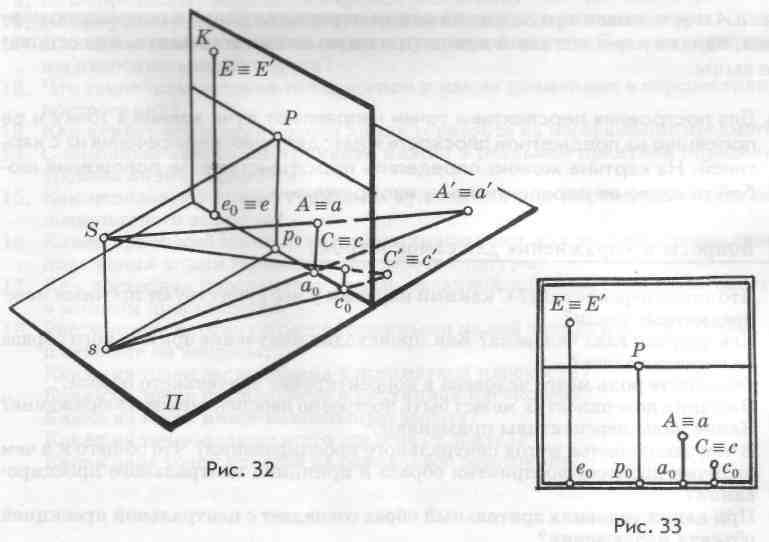
Положение точки называется частным, если она лежит в предметной или картинной плоскости, например, как точка В'. Точка Е' лежит в кар­тинной плоскости, об этом свидетельствует ее совпадение с перспективой Е' = Е) (рис. 32, 33). Она находится выше линии горизонта, слева от глав­ного вертикала. Точки А' з а' и С' = с лежат в предметной плоскости на раз-

ном расстоянии от картины. Точка С ближе точки А', поэтому ее перпен­дикуляр короче. На картине точка С = с находится ближе к основанию кар­тины, чемА^а.

27

Рассмотрим случай, когда точка общего положения расположена во мнимом пространстве, т. е. за спиной зрителя (рис. 34). Из точки зрения S проведем луч зрения через точку А' и продолжим его до пересечения с кар­тинной плоскостью. Соединим точку стояния s с основанием а' и продол­жим до пересечения с основанием картины, получим точку а₀. Из точки а₀ восстановим перпендикуляр, пересечение которого с прямой a'S опреде-

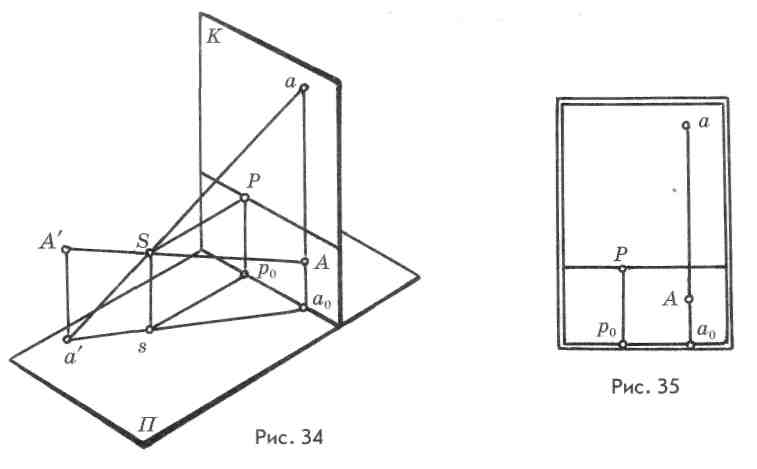
лит точку а. На картине (рис. 35) из построений видно, что перспектива точки А и ее основание а лежат на одном перпендикуляре к основанию кар­тины, однако перспектива А находится ниже линии горизонта, а ее основа­ние выше.

Для построения перспективы точки направляют лучи зрения в точку и ее проекцию на предметной плоскости и находят точки пересечения их с кар­тиной. На картине можно определить пространственное положение лю­бой точки по ее перспективному изображению.

| Вопросы и упражнения для самоконтроля

1. Что такое перспектива? С какими науками у нее существуют прочные меж­предметные связи?

2. Как устроен глаз человека? Как происходит получение зрительного образа на сетчатке глаза?

1. Объясните роль мозга человека в корректировке зрительного образа.

2. На каких поверхностях может быть построено перспективное изображение?

3. Какие виды перспективы применяют?

3. В чем заключается метод центрального проецирования? Что общего и в чем отличия процесса восприятия образа и принципа центрального проециро­вания?

4. При каких условиях зрительный образ совпадает с центральной проекцией объекта наблюдения?

28

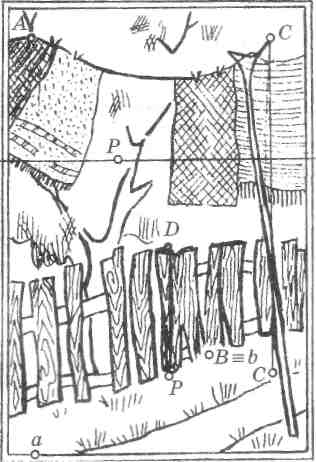
Рис.36

8. Как конусы видимости влияют на четкость восприятия?

9. Как определяют поле ясного зрения человека?

10. Какой угол зрения соответствует наилучшему восприятию натуры?

11. Назовите главные элементы проецирующего аппарата. Как они расположе­ны относительно друг друга?

12. Что такое совмещенная точка зрения и как ее применяют в перспективных построениях?

13. Как влияет изменение уровня линии горизонта на изображение предметов?

14. С помощью какого инструмента можно в реальной практике определить уровень линии горизонта?

15. Как используют линию горизонта художники для выражения своего ком­позиционного замысла?

16. Какое приспособление используют художники для выбора оптимального положения линии горизонта при работе с натуры?

17. Как построить перспективу точки, заданной в предметном пространстве, в мнимом пространстве?

18. Рассмотрите картину с расположенными на ней точками А, В, С, D (рис. 36) и ответьте на вопросы:

Какая из точек расположена в предметной плоскости? Какая из точек расположена в картинной плоскости? Какая из точек имеет наибольшую высоту? Какая из точек дальше всего удалена от зрителя? Какая пара точек удалена на одинаковое расстояние?

29