3. Перспектива тел в различных положениях

В учебных постановках и натюрмортах часто приходится изображать тела в различных положениях — ракурсах (рис. 190, 191).

На картине (рис. 192) показано построение горизонтально лежащего цилиндра, у которого заданы диаметр основания и высота (длина). Оба ос­нования цилиндра параллельны картинной плоскости, т. е. расположены фронтально. В этом случае для построения окружности способ описанного квадрата остается наиболее простым и удобным.

Отметим в предметной плоскости произвольно точку А и восстановим из нее перпендикуляр, на котором будет находиться вертикальный диаметр. Диаметр цилиндра определим с помощью масштаба высот, для этого на ос­новании картины проведем натуральную величину окружности и отметим ее центр. Перенесем размеры на картину и построим квадрат, в который впишем полную окружность и определим на ней точки СшЕ.

Используя дистанционную точку на основании картины, отложим на­туральную величину длины цилиндра и определим это расстояние в глуби-

121

Рис. 190

Рис.191 122

h D A» P h

H.B.

Рис. 192

не картины. Найдем точку А₁. Построим второй квадрат и впишем в него окружность, получив необходимое количество точек. Проведем очерковые прямые, которые являются касательными к окружностям и соприкасают­ся с ними в точках 1,2,3, 4.

В случае, когда основания цилиндра расположены перпендикулярно к картинной плоскости тоже используется способ вписанных окружностей. Построим четырехугольную призму, а затем в нее впишем цилиндр.

На картине (рис. 193) в предметной плоскости отметим произвольно точку А и найдем диаметр вертикального основания цилиндра с помощью масштаба высот. Соединив главную точку картины Р с основанием А полу-

н в Рис. 193

123

в ——ВТ

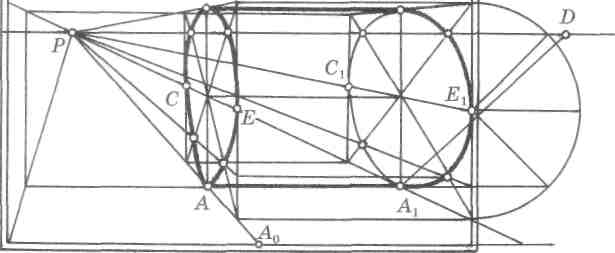
Рис. 194

чим картинный след Aq. Отложим на основании картины от точки Д, нату­ральную величину высоты цилиндра, соединим с точкой Р, получим точку А_х. Для построения основания 1-4-4^-1^ четырехугольной призмы соеди­ним точку А с дистанционной точкой D и продолжим до основания карти­ны. Получим точку А_в от которой по обе стороны отложим отрезки IqAd = A_D4₀, равные радиусу основания цилиндра. Соединим точку 1₀ и 4₀ с дис­танционной точкой. Получим точки 1 и 4, как точки пересечения прямых IqD и 4₀D с прямой AJP соответственно. Аналогично найдем точки 1₁ж4₁. Построим основание 2-3-3₁-2₁ и получим призму.

Построим в совмещенном положении половину окружности, найдем точки на диагоналях, перенесем их на оба основания призмы и построим цилиндр (рис. 194).

Более сложным случаем построения многогранников считается перс­пективное изображение треугольной пирамиды, у которой задана высота и основание (рис. 195).

На совмещенной плоскости вычерчена натуральная величина осно­вания ABC правильной треугольной пирамиды, вписанной в окружность. С помощью совмещенной точки зрения S_k найдем вершины А, Б, С и центр основания, которые получаются на пересечении лучей зрения, опущенных из точки S_k и глубинных прямых, направленных в точку Р. С помощью масштаба высоты определим вершину и проведем ребра пи­рамиды.

Построение призмы основано на построении цилиндра (рис. 196).

В предметной плоскости (рис. 197) задана произвольно точка А — сере­дина ребра шестиугольного основания призмы и направление бокового реб­ра. Определим точку схода F_lt для чего построим прямой угол при совме­щенной точке зрения S_k. Соединим точку F_t и А и продолжим до пересече-

124

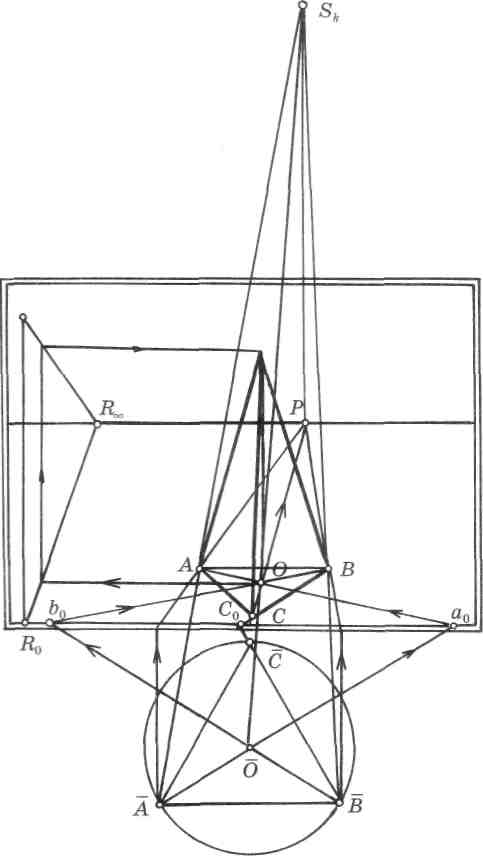
Рис. 195

ния с основанием картины в точке А₂, от которой отложим натуральную величину длины (высоты) призмы.

Продолжим прямую FzA и получим точку А₀ на основании картины. Построим половину натуральной величины шестиугольника, вписанного в окружность. Центр О и высоту шестиугольного основания определим, используя формулу AqO₀ = 0,8 d.

125

ч^

	ev.
/
vv 0l<		os \J
		■

Рис. 196

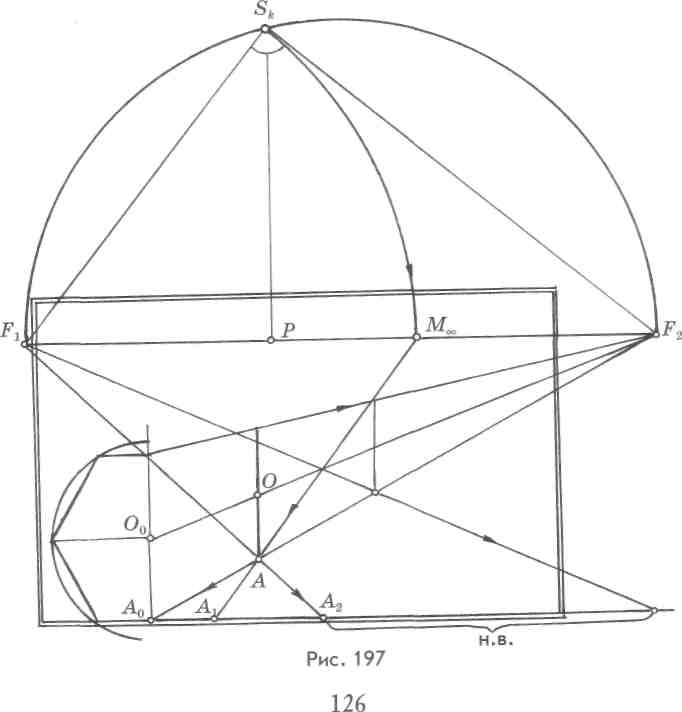
Построим масштабную точку М„ и выведем на основание картины точку Aj. Отложим в обе стороны от нее натуральные величины радиусов описанной вокруг шестиугольника окружности (рис. 198). Полученные точки соединим с масштабной, и найдем ширину шестиугольника в перспективе.

Построение геометрических тел в перспективе основано на приемах пост­роения плоских фигур и перспективных масштабов.