3. Перспектива многоугольников

Предметы окружающего мира в основе имеют форму простейших гео­метрических тел. При рисовании даже сложные формы человеческого тела могут быть упрощены до простых геометрических поверхностей. На пер­вых этапах обучения рисованию рекомендуется начинать с простых гео­метрических тел, где легче проследить перспективные и визуальные иска­жение формы в пространстве.

Рассмотрим примеры построения перспективы многоугольников, рас­положенных в различных положениях по отношению к картинной плоско­сти при доступных и недоступных точках схода.

На картине (рис. 153) параллельно ее основанию задана сторонаАВ квад­рата. Требуется построить квадрат, расположенный в предметной плоскости.

94

0 10 20 30 40

Рис. 153 Рис. 154

При вершинах А и В построим прямые углы, для чего проведем глубин­ные прямые АР и ВР. Через вершину А (или В) проведем диагональ, пре­дельной точкой которой является дистанционная. Точка С на прямой АР определит положение стороны СЕ искомого квадрата.

Изображение квадратов таким способом используется при построении паркетов прямоугольной формы.

На основании картины (рис. 154) заданы стороны 01₀, 1₀2₀, 2₀3₀, 3₀4 квадратных плит. Требуется построить перспективное изображение части пола, выложенного такими плитами.

Построим глубинные прямые сторон квадрата с главной точкой схо­да Р. Через точку 0 и D проведем диагональ квадратов, которая в пересече­нии с каждой глубинной прямой отметит точки 1,2,3,4. Через отмеченные точки проведем горизонтальные прямые, параллельные основанию карти­ны. Они определят перспективу квадратных плит, расположенных в плос­кости пола.

Поскольку предметную плоскость можно поворачивать и совмещать с картиной как вверх, так и вниз, то можно задать форму и размеры паркета в совмещенной плоскости внизу листа (рис. 155). Паркет может иметь бо­лее сложный рисунок, который хорошо вписывается в квадрат.

На картине (рис. 156) задана вертикальная сторона АВ квадрата. Тре­буется построить квадрат, который расположен перпендикулярно картин­ной и предметной плоскости.

Направлением сторон прямого угла при вершинах А и Б будут глубин­ные прямые АР и ВР. Чтобы отложить на них стороны квадрата, приведем АВ в горизонтальное положение АВ₁ и перенесем его величину при помощи дистанционной точки на глубинную прямую АР. Точка С определит конец стороны СЕ квадрата.

На картине (рис. 157) сторона АВ квадрата вертикальная. Требуется построить квадрат, расположенный перпендикулярно к предметной плос­кости и под произвольным углом к картине.

95

Рис.155

Стороны квадрата, перпендикулярные к АВ, лежат на прямых, предель­ной точкой которых может быть любая точка линии горизонта, например А^. Величину стороныЛС квадрата определим при помощи масштабной точ­ки М„. Затем через точку С проведем вертикальную сторону СЕ квадрата.

Эти приемы построения квадрата можно использовать при изображе­нии треугольников в вертикальных плоскостях (рис. 158). Оба квадрата имеют одну и ту же предельную и масштабную точки. При сравнении они производят разное визуальное впечатление, хотя имеют одинаковые гео­метрические параметры.

Рис. 156 Рис.157

96

N.			Г"--—£
			p 1				' ^D~
	*-. -; • • V. ? »- • •*« i j^			■*-"■%	Cy>	—^—-^
'	A

Рис. 158

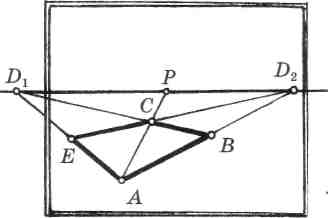
На картине (рис. 159) сторона АВ квадрата лежит в предметной плос­кости. Ее предельной точкой является дистанционная точка D₂. Требуется построить квадрат, лежащий в предметной плоскости.

Стороны прямых углов при вершинах А и В лежат на прямых с точкой схода D_x Чтобы определить положение четвертой стороны квадрата, най­дем вершину С. Она лежит на диагонали квадрата с предельной точкой Р.

На картине (рис. 160) задана большая сторона АВ прямоугольника с предельной точкой D₂. Требуется построить прямоугольник, лежащий в предметной плоскости.

А	щ... ■■_■■ щ -=Z. р	А.	D.
^	^	&>	^

Рис. 159

Рис. 160

7 Э-298

97

Рис. 161

73

Построение прямоугольника аналогично построению квадрата. Здесь предельной точкой диагонали квадрата будет любая точка А„ на линии го­ризонта и справа от главной точки Р.

Этим построением можно воспользоваться при построении паркета, выложенного прямоугольными плитами или елочкой. Форма и размеры паркета заданы в совмещенной плоскости внизу листа (рис. 161).

При построении перспективы паркета форма плитки может быть раз­ной, но принцип построения одинаковый (рис. 162), даже если паркет име­ет форму правильного шестиугольника, который необходимо изобразить с учетом перспективных сокращений.

При построении шестиугольника, лежащего в предметной плоскости и параллельного одной стороной основанию картины, угол при совмещенной точке зрения S_k образуется прямыми параллельными сторонам этого шес­тиугольника и составляет 60° (рис. 163).

Однако, в перспективе часто приходится изображать треугольники, которые расположены в предметной плоскости с произвольно расположен­ными сторонами. В этом случае целесообразней применять способ совме­щения.

98

Рис. 162

		i	5,
/ fJ			\ p \p2
		%?	iff^ii
			Щ
		\ •"."	h"'TAw

Рис. 163

99

Рис. 164

Построим треугольник ABC, натуральная величина которого задана в совмещенной плоскости (рис. 164). Проведем несовмещенной точки зрения прямые параллельные сторонам треугольника АВ и ВС, S_kF_l \\AB и S^ || ВС, и получим точки схода i*\ и F₂. Для построения перспективного изображе­ния треугольника продолжим стороны АВ и ВС до пересечения с основани­ем картины в точках а₀ и с₀. Соединим полученные точки с точками схода. Из совмещеннойточки зрения S_k проведем лучи зрения_в каждую вершину треугольника ABC. При пересечении прямых a₀F₂ ^c &iA получим вершину А перспективного изображения треугольника. Аналогично получим все остальные вершины.

► Построение плоских фигур может осуществляться разными способами, из которых выбирают самый оптимальный, требующий меньше построе­ний и дающий больше наглядности.

100