
- •Контрольная работа №3 для зис11
- •Задание 3. Найти объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями:
- •Задание 4. Вычислить двойной интеграл по области d, ограниченной заданными линиями (область d изобразить на чертеже).
- •Контрольная работа №4
- •Задание 3. Найти все значения z и изобразить их на комплексной плоскости:
- •Задание 4. Проверить выполнение условий Коши-Римана и там, где они выполняются, найти производные:
- •Варианты №8,9,10
Контрольная работа №3 для зис11
Задание №1. Найти неопределённые интегралы. В п. а) и б) результаты проверить дифференцированием.
а)
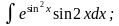 б)
б)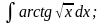 в)
в)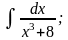 г)
г)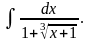
а)
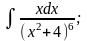 б)
б)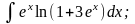 в)
в)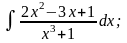 г)
г)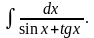
а)
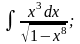 б)
б)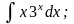 в)
в)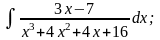 г)
г)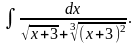
а)
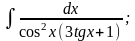 б)
б)
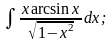 в)
в)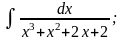 г)
г)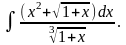
а)
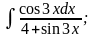 б)
б)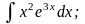 в)
в)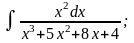 г)
г)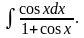
а)
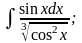 б)
б)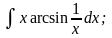 в)
в)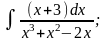 г)
г)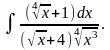
а)
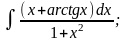 б)
б)
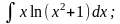 в)
в)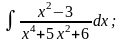 г)
г)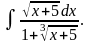
а)
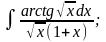 б)
б)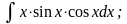 в)
в)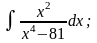 г)
г)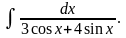
а)
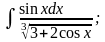 б)
б)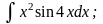 в)
в)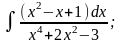 г)
г)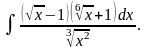
а)
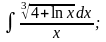 б)
б)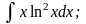 в)
в)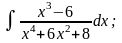 г
г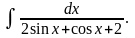
Задание 3. Найти объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями:
Вариант 1. y = x2; у = 0; х = 1; х = 2.
Вариант
2. y = x3;
у =
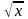 .
.
Вариант 3. y = 2x-x2; у =-x+2 ; х = 0.
Вариант
4.
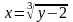 ;
у =1 ; х = 1.
;
у =1 ; х = 1.
Вариант
5.
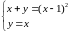 .
.
Вариант
6.
 ;
у =0 ; х = 0.
;
у =0 ; х = 0.
Вариант
7.
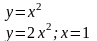 .
.
Вариант
8.
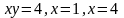 ;
у =0.
;
у =0.
Вариант
9.
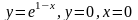 ;
x =1.
;
x =1.
Вариант 10.
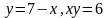 .
.
Задание 4. Вычислить двойной интеграл по области d, ограниченной заданными линиями (область d изобразить на чертеже).
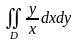 ,
где D:
,
где D:
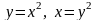
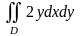 ,
где D:
,
где D:
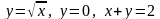
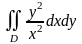 ,
где D:
,
где D:
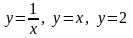
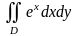 ,
где D:
,
где D:
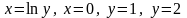
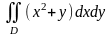 ,
где D:
,
где D:
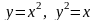
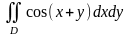 ,
где D:
,
где D:

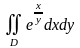 ,
где D:
,
где D:
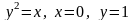
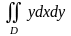 ,
где D ограничена осью Ох
и одной аркой циклоиды
,
где D ограничена осью Ох
и одной аркой циклоиды
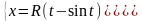
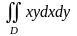 ,
где D ограничена осями
координат и дугой астроиды
,
где D ограничена осями
координат и дугой астроиды
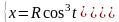
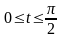
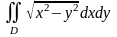 ,
где D – треугольник с вершинами О(0;0),
А(1;-1), В(1;1).
,
где D – треугольник с вершинами О(0;0),
А(1;-1), В(1;1).
Задание №4. Исследовать сходимость рядов.
а)
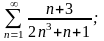 б)
б)
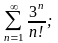 в)
в)
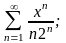 г)
г)

а)
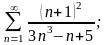 б)
б)
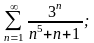 в)
в)
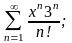 г)
г)
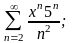
а)
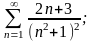 б)
б)
 в)
в)
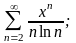 г)
г)
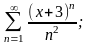
а)
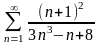 б)
б)
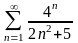 в)
в)
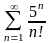 г)
г)
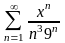
а)
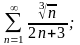 б)
б)
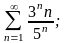 в)
в)
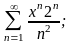 г)
г)
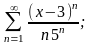
а)
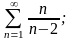 б)
б)
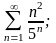 в)
в)
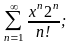 г)
г)
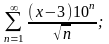
а)
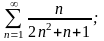 б)
б)
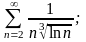 в)
в)
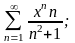 г)
г)
а)
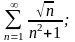 б)
б)
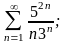 в)
г)
в)
г)
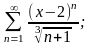
а)
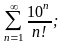 б)
в)
б)
в)
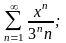 г)
г)
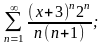
а)
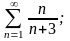 б)
б)
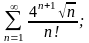 в)
в)
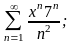 г)
г)
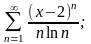
Контрольная работа №4
Задание 1. Найти общее решение дифференциального уравнения:
Вариант 1. А.
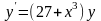 ; Б.
; Б.
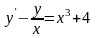 ;
;
Вариант 2. А.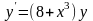 ;
Б.
;
Б.
 ;
;
Вариант 3. А.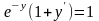 ;
Б.
;
Б.
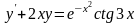 ;
;
Вариант 4. А.
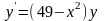 ; Б.
; Б.
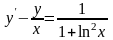 ;
;
Вариант 5. А.
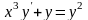 ; Б.
;
; Б.
;
Вариант 6. А.
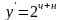 ; Б.
; Б.
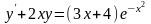 ;
;
Вариант 7. А.
 ; Б.
; Б.
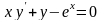 ;
;
Вариант 8. А.
; Б.
 ;
;
Вариант 9. А.
 ; Б.
; Б.
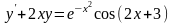 ;
;
Вариант10. А.
 ; Б.
;
; Б.
;
Задание 2. Решить неоднородные линейные уравнения второго порядка:
А.
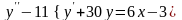 Б.
Б.
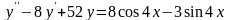 .
.А.
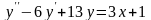 Б.
Б.
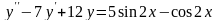 .
.А.
 Б.
Б.
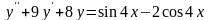 .
.А.
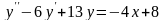 Б.
Б.
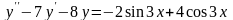 .
.А.
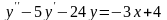 Б.
Б.
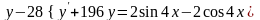 .
.А.
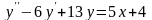 Б.
Б.
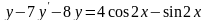 .
.А.
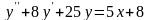 Б.
Б.
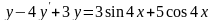 .
.А.
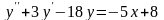 Б.
Б.
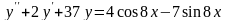 .
.А.
 Б.
Б.
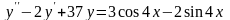 .
.А.
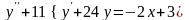 Б.
Б.
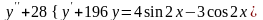 .
.
Задание 3. Найти все значения z и изобразить их на комплексной плоскости:
Вариант
1 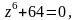
Вариант 2 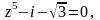
Вариант 3 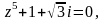
Вариант 4 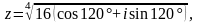
Вариант 5 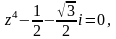
Вариант 6 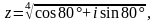
Вариант 7 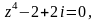
Вариант 8 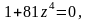
Вариант 9 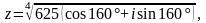
Вариант 10 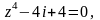
Задание 4. Проверить выполнение условий Коши-Римана и там, где они выполняются, найти производные:
Вариант 1 
Вариант 2 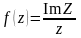
Вариант 3 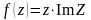
Вариант 4 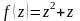
Вариант 5 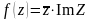
Вариант 6 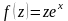
Вариант 7 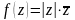
Вариант 8 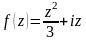
Вариант 9 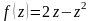
Вариант 10 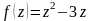
Задание 5. Операции над событиями:
Вариант 1. В цеху - три независимо работающих линии. Вероятности того, что в случайный момент времени загружены: 1-ая линия равна 0,9; вторая - 0,8; третья -0,7. Найти вероятности того, что в случайный момент времени:
А- загружены две линии;
В- хотя бы одна линия свободна;
С- все линии свободны.
Вариант 2. Цех имеет три независимо работающих конвейерные линии.
Вероятности сбоя в работе в течение часа: для 1-й линии - 0,1 , для 2-й - 0,05, для 3-
й - 0,08. Найти вероятности того, что в течение часа:
А- ни на одной из линий сбоя не произойдет;
В- сбой произойдет не более чем на одной линии;
С - сбой произойдет точно на одной линии.
Вариант 3. Станция скорой медицинской помощи небольшого микрорайона имеет
три реанимационные бригады. Вероятность того, что в любой момент времени
заняты: 1-я бригада равна 0,5, 2-я - 0,6, 3-я - 0,7. Найти вероятность того, что в
случайно выбранный момент времени:
А- все бригады заняты;
В- хотя бы одна бригада свободна;
С- свободны две бригады из трех.
Вариант 4. В речном порту - три причала. Вероятности того, что причал занят равны: для 1-го причала - 0,9, для 2-го - 0,8, для 3-го - 0,7. Найти вероятности того, что в случайный момент времени: А- все три причала заняты; В- занят только один причал; С- хотя бы один причал свободен.
Вариант 5. В аэропорту три взлетно-посадочные полосы. Вероятности того, что
взлетно-посадочные полосы свободны, равны: для 1-й полосы - 0,8, для 2-й - 0,7,
для 3-й - 0,6. Найти вероятности событий:
А- хотя бы одна взлетно-посадочная полоса свободна;
В- свободны точно две полосы;
С - все полосы заняты.
Вариант 6. Телефонная станция обслуживает три микрорайона города. Вероятность
того, что в течение суток произойдет сбой в 1-м микрорайоне равна 0,1, во 2-м -
0,15, в 3-м- 0,12. Найти вероятности того, что в течение
суток:
А- ни в одном микрорайоне не произойдет сбой;
В- сбой произойдет не более чем в одном микрорайоне;
С - сбой произойдет точно в одном микрорайоне.
Вариант 7. Конвейер содержит три одинаковые, независимо работающие линии. Вероятность того, что в данный момент времени занята каждая линия равна 0,8. Найти вероятности того, что в случайный момент времени: А- свободна хотя бы одна линия; В- свободны точно две линии; С - все линии заняты.
Вариант 8. Конвейер содержит три одинаковые, независимо работающие линии. Вероятность того, что в данный момент времени занята каждая линия равна 0,8. Найти вероятности того, что в случайный момент времени: А- свободна хотя бы одна линия; В- свободны точно две линии; С - все линии заняты.
Вариант 9. Три стрелка производят по одному выстрелу. Вероятности попадания
для каждого стрелка соответственно равны: 0,7, 0,85 и 0,8. Найти вероятности
того, что:
А- попали точно два стрелка;
В- попал хотя бы один стрелок;
С- попали не менее двух стрелков.
Вариант 10. Три охотника отправились "на кабана". Вероятности заполучить добычу
для них соответственно равны 0,4, 0,6 и 0,7. Найти вероятности того, что:
А- все три охотника вернулись с добычей;
В- хотя бы один охотник вернулся с добычей;
С- не более одного охотника вернулись с добычей.
Задание 6. Формула полной вероятности:
Вариант 1. Строительная компания, в которой два управления, ведет застройку микрорайона. Вероятности того, что наудачу взятый объект, выполняемый первым управлением, будет сдан в эксплуатацию досрочно, равна 0,9 , вторым -0,8. Первое управление выполняет 60% всех работ, второе - 40% . Найти вероятность того, что наудачу взятый объект микрорайона будет сдан в эксплуатацию досрочно.
Вариант 2. При работе компьютера вероятность сбоя в арифметика - логическом устройстве - 0,3, в оперативной памяти - 0,2, в остальных устройствах - 0,5. Вероятности обнаружения сбоя: в арифметико-логическом устройстве - 0,95, в оперативной памяти - 0,85, в остальных устройствах - 0,9. Возникший в компьютере сбой был обнаружен. Найти вероятность того, что этот сбой произошел в оперативной памяти.
Вариант 3. На станции технического обслуживания автомобилей работают две бригады: в первой - 8 механиков, во второй - 4. Вероятность того, что автомобиль, попавший в первую бригаду, будет обслужен отлично, равна 0,7, а во вторую - 0,9. Прибывший на станцию автомобиль был обслужен отлично. Найти вероятность того, что им занималась первая бригада.
Вариант 4. Завод имеет 60% технологических линий 1-го типа и 40%- линий 2-го типа. Если деталь попадет на линию 1-го типа, то вероятность брака равна 0,1, для линии 2-го типа - 0,3. Найти вероятность того, что случайно выбранная деталь окажется бракованной.
Вариант 5. Система контроля за качеством представляет собой 6 аппаратов первого вида и 4 аппарата второго вида. Каждая деталь случайным образом попадает на проверку в один из аппаратов. Аппарат первого вида обнаруживают бракованную деталь с вероятностью 0,75, а второго вида - 0,9. Бракованная деталь была обнаружена. Найти вероятность того, что она проходила проверку аппаратом первого вида.
Вариант 6. На АЗС три линии обслуживания. На 1-й линии 2^ заправочные колонки, на 2-й - 4, на 3-й - 2. Если автомобиль подъедет к 1-й линии, то вероятность заправиться в течение 15 минут равна 0,9, если подъедет ко 2-й, то эта вероятность - 0,7, если к 3-й, то - 0,8. Найти вероятность того, что автомобиль, подъехавший к АЗС заправится в течение 15 минут.
Вариант 7. На разгрузочно-погрузочной станции два железнодорожных пути. Вероятность того, что вагон попадет на 1-й путь равна 0,6, на 2-й - 0,4. ./' Вероятность того, что вагон будет разгружен в течение 30 минут равна 0,9, если он окажется на первом пути и 0,8, если на втором. Доставленный на станцию вагон был разгружен в течение 30 минут. Найти вероятность того, что вагон обслуживался на втором пути.
Вариант 8. Детали изготавливаются на двух заводах, причем первый завод выпускает 70%, а второй 30%, Вероятность того, что деталь окажется бракованной равна 0,1, если сделана на первом заводе и 0,05, если на втором. Найти вероятность того, что наудачу взятая деталь окажется качественной.
Вариант 9. . По военному объекту производится пуск двух ракет. Вероятность попадания в него первой ракеты равна 0,75, второй ракеты - 0,85.^ Вероятность уничтожения объекта при попадании в него одной ракеты равна 0,5,. а при попадании двух ракет - 0,95. В результате пуска обеих ракет объект был уничтожен. Найти вероятность того, что в объект попала лишь одна бомба.
Вариант 10. Корабль, атакованный подводной лодкой, был потоплен одной торпедой. Вероятность попадания торпеды в носовую часть корабля - 0,25, в среднюю - 0,4, в кормовую - 0,35. Вероятности потопления корабля при попадании торпеды в каждую из его частей соответственно равны: 0,4, 0,9 и 0,5. Найти вероятность того, что торпеда попала в корму.
Задание 7. Схема повторных испытаний Бернулли:
Вариант 1. В парикмахерской работают 6 мастеров. Вероятность того, что каждый из них занят в данный момент, равна 0,8. Найти наивероятнейшее число занятых мастеров. Определить вероятность того, что хотя бы один мастер свободен.
Вариант 2. В мастерской по ремонту обуви работают-7 мастеров. Вероятность того, что каждый мастер в случайный момент времени занят, равна 0,6. Найти наивероятнейшее число занятых мастеров. Определить вероятность того, что в данный момент занято не более двух мастеров.
Вариант 3. В аэропорту 5 взлетно-посадочных полос. Вероятность того, что в некоторый момент времени каждая полоса занята, равна 0,7. Найти наивероятнейшее число занятых полос. Определить вероятность того, что в данный момент можно посадить точно два самолета.
Вариант 4. В ателье работают 5 мастеров. Вероятность того, что в некоторый момент времени каждый из мастеров занят, равна 0,85. Найти наивероятнейшее число занятых мастеров. Определить вероятность того, что в этот момент свободны точно три мастера.
Вариант 5. В аэропорту 6 взлетно-посадочных полос. Вероятность того, что каждая из полос занята, равна 0,7. Найти наивероятнейшее число занятых полос. Определить вероятность того, что в данный момент можно посадить хотя бы два самолета.
Вариант 6. Станция технического обслуживания автомобилей имеет 6 боксов. Вероятность того, что в случайный момент времени занят каждый из боксов, равна 0,8. Найти наивероятнейшее число занятых боксов. Определить вероятность того, что в случайный момент свободны точно три бокса.
Вариант 7. В аэропорту 5 взлетно-посадочных полос. Вероятность того, что каждая из полос в случайный момент времени занята, равна 0,65. Найти наивероятнейшее число занятых полос. Определить вероятность того, что что хотя бы одна полоса свободна.
Вариант 8. На станции технической помощи автомобилям имеется 5 аварийных машин. Вероятность того, что в случайный момент времени каждая из этих машин занята, равна 0,55. Найти наивероятнейшее число занятых аварийных машин. Найти вероятность того, что хотя бы одна машина свободна.
Вариант 9. На железнодорожном вокзале имеется 7 путей. Вероятность того, что в случайный момент времени каждый из путей занят, равна 0,7. Найти наивероятнейшее число занятых путей. Определить вероятность того, что подошедший в этот момент поезд будет принят без задержки.
Вариант 10. В массажном кабинете работают 4 мастера. Вероятность того, что каждый из них занят в данный момент, равна 0,8. Найти наивероятнейшее число занятых мастеров. Определить вероятность того, что хотя бы один мастер свободен.
Задание 8. Найти вероятность безотказной работы цепи, если известна надежность каждого участка:
Вариант 1.
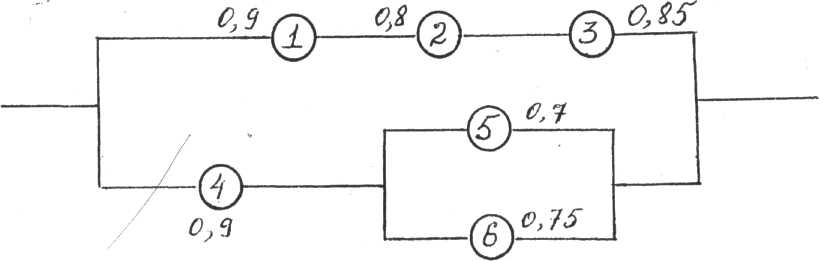
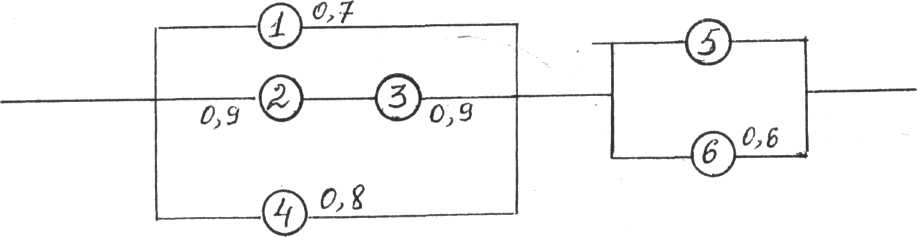
Вариант 2.
Вариант 3.
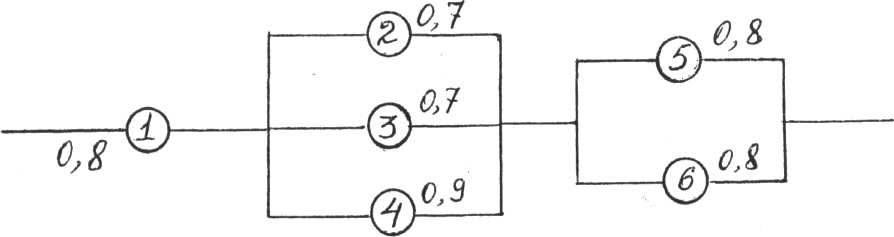
Вариант 4.
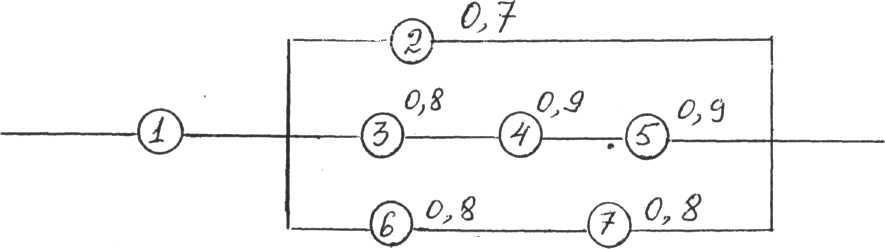
Вариант 5.
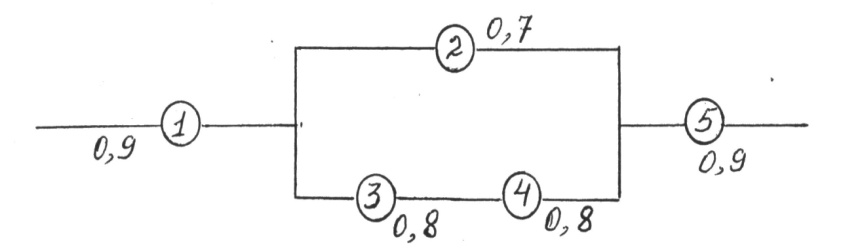
Вариант 6.
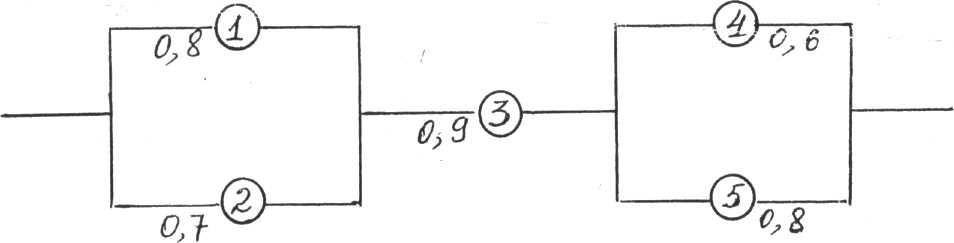
Вариант 7.
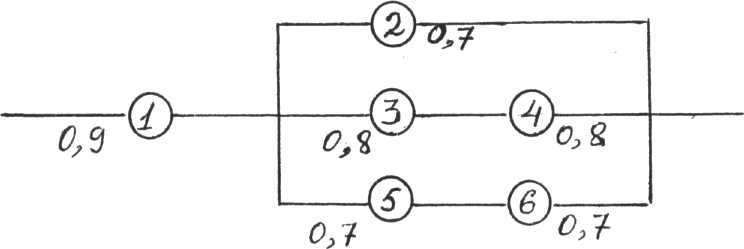
Вариант 8.
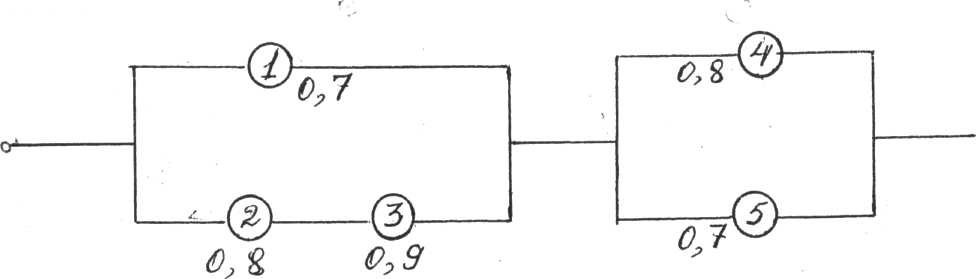
Вариант 9.
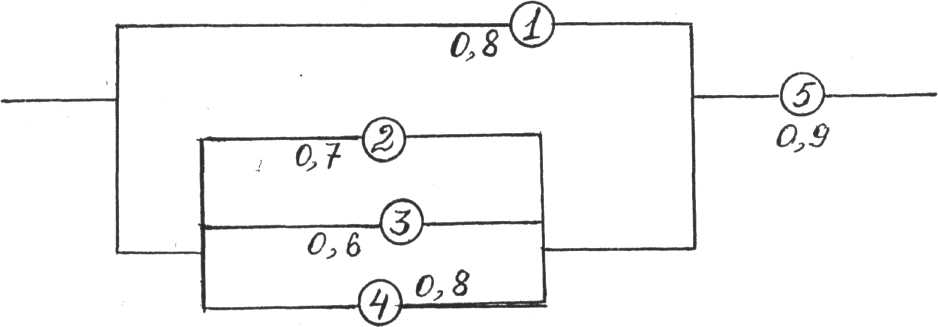
Вариант 10.
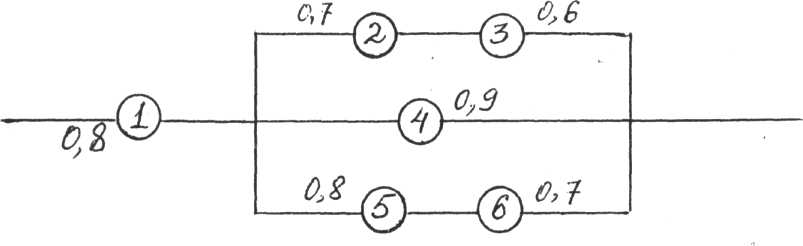
Задание №9. Дискретные случайные величины
Составить закон распределения случайной величины Х. Записать функцию распределения, построить её график. Вычислить числовые характеристики М(Х), D(Х), s(Х)).
Варианты №1,2,3,4
Х-число отказавших элементов в одном опыте с устройством, состоящим из n независимо работающих элементов. Вероятность отказа каждого элемента р.
1. n=3, p=0.1.
2. n=4, p=0.15.
3. n=3, p=0.15.
4. n=4, p=0.2.
Варианты №5,6,7
В партии k% бракованных изделий. Наудачу отобрано n изделий. Х- число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону:
5. k=15%, n=4.
6. k=10%, n=5.
7. k=20%, n=3.
Варианты №8,9,10
В партии из n деталей имеется m стандартных. Наудачу отобрали k деталей. Х-число стандартных деталей среди отобранных.
8. n=10, m=8, k=3.
9. n=9, m=7, k=3.
10. n=12, m=10, k=3.
Задание №10. Непрерывные случайные величины: равномерное, нормальное и показательное распределения:
Варианты №1,2, 3
Цена деления шкалы амперметра равна a Ампер. Показания амперметра округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка, меньшая e.
1. a=0.1, e=0.04.
2. a=0.2, e=0.05.
3. a=0.1, e=0.02.
Варианты №4,5,6,7
Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально. Проектная длина детали равна l мм. Фактическая длина изготовленных деталей не менее a мм и не более b мм. Найти вероятность того, что длина наудачу взятой детали меньше а мм.
4. l=50, a=32, b=68, а=40.
5. l=100 a=80, b=120, а=90.
6. l=80 a=70, b=90, а=75.
7. l=200 a=160, b=240, а=190.
