Элементы прямоугольного сечения Расчет на совместное действие крутящего крутящего и изгибающего моментов

3.77. Расчет по прочности элемента между пространственными сечениями на действие крутящего момента Т производят из условия

T < 0,lRbb2h,                                                                                              (3.152)

где b и h - соответственно меньший и больший размеры поперечного сечения элемента.

3.78. При совместном действии крутящего и изгибающего моментов рассматривается пространственное сечение со сжатой стороной по грани элемента, перпендикулярной плоскости действия изгибающего момента (черт.3.40).

Расчет такого сечения производят из условия

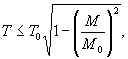                                                                                   (3.153)

 

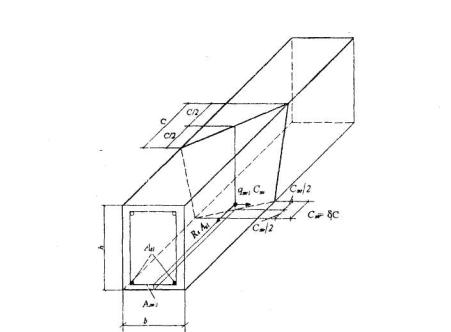
Черт.3.40. Схема усилий в пространственных сечениях при расчете на действие крутящего и изгибающего моментов; растянутая арматура у нижней границы элемента

где Му - предельный изгибающий момент, воспринимаемый нормальным сечением и определяемый согласно п.3.14;

Т0 - предельный крутящий момент, воспринимаемый пространственным сечением и определяемый по формуле

T0 = Tsvl + Ts1,                                                                                            (3.154)

Tsvl - крутящий момент, воспринимаемый поперечной арматурой, расположенной у растянутой грани в пределах пространственного сечения, равный

Tswl= 0,9qswlδ1ch,                                                                                      (3.155)

Ts1 - крутящий момент, воспринимаемый продольной растянутой арматурой пространственного сечения и равный

Tsl = 0,9RsAs1(b/c)h.                                                                                  (3.156)

В формулах (3.155) и (3.156):

с - длина проекции сжатой стороны пространственного сечения на продольную ось элемента;

                                                                                             (3.157)

b и h - соответственно ширина грани, растянутой от изгиба, и грани, ей перпендикулярной (см. черт.3.40);

                                                                                       (3.158)

Asw1 и sw - площадь сечения одного поперечного стержня у растянутой от изгиба грани шириной b и шаг этих стержней;

As1 - площадь сечения продольной арматуры у растянутой от изгиба грани шириной b.

Значение RsAs1 в формуле (3.156) принимается не более значения 2qsw1b, а значение qsw1 в формуле (3.155) принимается не более значения 1,5RsAs1/b.

Крутящий момент Т и изгибающий момент М в условии (3.153) принимаются в поперечном сечении, расположенном в середине длины проекции с вдоль продольной оси элемента.

Расчет в общем случае производят для пространственных сечений с различными значениями с, принимаемыми не более 2h + b и не более .

Пространственные сечения рекомендуется располагать следующим образом:

а) для неразрезных или защемленных на опорах балок (ригелей), а также для консолей пространственное сечение располагается у опоры;

б) для любых элементов, нагруженных сосредоточенными силами и крутящими моментами, пространственные сечения располагаются у мест приложения сил со стороны участка с большими крутящими моментами (черт.3.41).

Для этих случаев при вычислении предельного крутящего момента То рекомендуется использовать в формулах (3.155) и (3.156) значение длины проекции с = сo, соответствующее минимальному значению То, но при этом моменты Т и М определяются исходя из длины проекции равной с = (1,2 - 0,4Mmax/Mo)сo, но не более сo, где Mmax - максимальный изгибающий момент в начале пространственного сечения.

Значение сo определяется по формуле

 ,                                                                              (3.159)

с выполнением указанных ограничений по учету величия RsAs1 и qsw1.

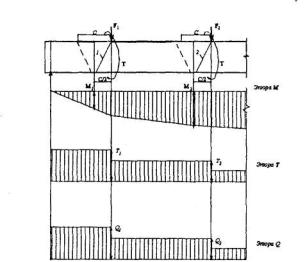
Черт.3.41. Расположение расчетных пространственных сечений в балке, нагруженной сосредоточенными силами

1, 2 -расчетные пространственные сечения;

M1,T1, Q1 - расчетные усилия для пространственного сечения 1;

M2,T2, Q2 - тo же, для пространственного сечения 2

В частности:

- при RsAs1 ≥ 2qsw1b формула (3.159) принимает вид 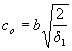, и тогда

;                                                                                 (3.160)

- при RsAs1 < 2qsw1b < 3 RsAs, значение Тo после подстановки с = сo равно

  ;                                                                            (3.161)

в) для элементов, нагруженных равномерно распределенной нагрузкой, если в пролетном сечении с наибольшим изгибающем моментом имеет место крутящий момент, середина проекции с располагается в указанном поперечном сечении; в этом случае невыгоднейшее значение с принимается равным сo.