Расчет нормальных сечений по предельным усилиям Прямоугольные сечения с симметричной арматурой
3.56 Проверку прочности прямоугольных сечений с симметричной арматурой (когда RsAs = RscA's) производят из условия
М ≤ Rbbx(hо - 0,5x) + (RscA's - N/2)(hо - а'), (3.91)
где М - момент относительно центра тяжести сечения, определяемый с учетом прогиба элементов согласно пп.3.53-3.55;
х - высота сжатой зоны, принимаемая равной
а)
при
;(черт.3.27)
б) при aп > ξR - х = ξ·hо,
где ξ определяется по формуле
(3.92)
здесь
ξR - см. табл. 3.2.
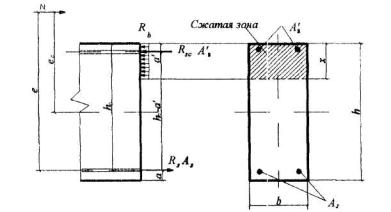
Черт.3.27. Схема усилий в поперечном прямоугольном сечении внецентренно сжатого элемента
3.57.
Требуемое количество симметричной
арматуры определяется следующим образом
в зависимости от относительной величины
продольной силы
а) при aп ≤ ξR
(3.93)
б) при aп > ξR
(3.94)
где ξ - относительная высота сжатой зоны, определяемая по формуле (3.92), где значение as допускается принимать равным
(3.95)
М - см. пп.3.53-3.55.
Если значение a' не превышает 0,15ho необходимое количество арматуры можно определять с помощью графика черт.3.28, используя формулу
(3.96)
где аs определяется по графику черт.3.28 в зависимости от значений
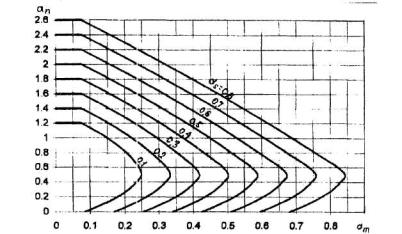
Черт.3.28. Графики несущей способности внецентренно сжатых элементов прямоугольного сечения с симметричной арматурой
3.58. Расчет сжатых элементов из бетона классов В15-В35 на действие продольной силы, приложенной с эксцентриситетом, принятым согласно п.3.49, равным случайному эксцентриситету еo = h/30, при lo < 20h допускается производить из условия
N ≤ φ(RbA + RscAs,tot), (3.97)
где φ - коэффициент, определяемый по формуле
φ = φb+2(φsb- φb)as, (3.98)
но принимаемый не более φsb.
Здесь φb и φsb - коэффициенты, принимаемые по табл. 3.5 и 3.6.
Таблица 3.5
|
Коэффициент φb при lo/h |
|||||||
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0.88 |
0,86 |
0,84 |
0,5 |
0,92 |
0,91 |
0,90 |
0,89 |
0,86 |
0,82 |
0,77 |
0,71 |
1,0 |
0,92 |
0,91 |
0,89 |
0,87 |
0,83 |
0,76 |
0,68 |
0,60 |
Таблица 3.6.
|
Коэффициент φsb при lo/h |
|||||||
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
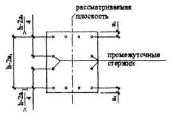
А. При а = а' < 0,15h и при отсутствии промежуточных стержней (см. эскиз) или площади сечения этих стержней менее Аs,tot/3 |
||||||||
0 |
0,93 |
0,92 |
0,91 |
0,90 |
0,89 |
0,88 |
0,86 |
0,83 |
0,5 |
0,92 |
0,91 |
0,91 |
0,90 |
0,88 |
0,87 |
0,83 |
0,79 |
1,0 |
0,92 |
0,91 |
0,90 |
0,90 |
0,88 |
0,85 |
0,80 |
0,74 |
Б. При 0,25h > а = а' ≥ 0,15h или при площади промежуточных стержней (см. эскиз), равной или более Аs,tot/3 независимо от а |
||||||||
0 |
0,92 |
0,92 |
0,91 |
0,89 |
0,87 |
0,85 |
0,82 |
0,79 |
0,5 |
0,92 |
0,91 |
0,90 |
0,88 |
0,85 |
0,81 |
0,76 |
0,71 |
1,0 |
0,92 |
0,91 |
0,89 |
0,87 |
0,83 |
0,77 |
0,70 |
0,62 |
|
Обозначения, принятые в табл. 3.5 и 3.6: N1 - продольная сила от действия постоянных и длительных нагрузок. N - продольная сила от всех нагрузок. |
|||||||
(3.99)
As,tot - площадь сечения всей арматуры в сечении;
при as > 0,5 можно, не пользуясь формулой (3.98), принимать φ = φsb