
Ууууууууууу
Умови
Коші-Рімана для функції
мають вид: г)
![]() ;
Г .
;
Г .
Ффффффффффффффф
Формула Гріна встановлює зв’язок між: б) подвійними і криволінійними інтегралами; Б .
Формула
Гріна має вид (![]() -
замкнений контур, що
обмежує
область
і обходиться в додатному напрямі):
в)
-
замкнений контур, що
обмежує
область
і обходиться в додатному напрямі):
в)
![]() ;
В .
;
В .
Формула Остроградського-Гаусса встановлює зв’язок між: г) потрійними і поверхневими інтегралами; Г .
Формула
Остроградського-Гаусса має вид (
![]() ,
- замкнена поверхня, що обмежує область
): а)
,
- замкнена поверхня, що обмежує область
): а)
![]() ;
А .
;
А .
Формула Стокса встановлює зв’язок між: а) криволінійними і поверхневими інтегралами; А .
Формула
Стокса має вид (
,
- замкнений
контур, що обмежує поверхню
):
в)
![]() ;
В .
;
В .
Функція
![]() буде аналітичною в деякій області, якщо
в цій області вона: б) має неперервну
похідну;
Б
.
буде аналітичною в деякій області, якщо
в цій області вона: б) має неперервну
похідну;
Б
.
Функція
![]() називається гармонічною, якщо: а)
називається гармонічною, якщо: а)
![]() ;
А
.
;
А
.
Циркуляція
вектора
вздовж
замкненого
контура
знаходиться за формулою:
г)
Ц![]() ;
Г .
;
Г .
Чччччччччч
Число
![]() є границею послідовності
є границею послідовності
![]() ,
якщо: в)
,
якщо: в)
![]() ;
В
.
;
В
.
Числовий ряд збігається, якщо: а) існує скінченна границя послідовності частинних сум ряду;
Яяяяяяяяяя
Яка з
наведених нижче рівностей невірна: б)
![]() ;
Б
.
;
Б
.
Яка з
наведених нижче рівностей невірна: в)
![]() ;
В
.
;
В
.
Яка з
наведених нижче рівностей невірна: в)
![]() ;
В
.
;
В
.
Яка з
наведених нижче формул для похідної
аналітичної функції
є невірною: 2)
![]()
![]() ;
б) тільки 2; Б
.
;
б) тільки 2; Б
.
Яка з
умов гарантує збіжність ряду
![]() ? б)
? б)
![]() - неперервна, спадна,
- неперервна, спадна,
![]() ;
;
Яка з
умов гарантує збіжність ряду
?
в)
![]() ;
В .
;
В .
Яка з
умов гарантує збіжність ряду
?
а)
![]() ;
А .
;
А .
Яка з умов гарантує збіжність ряду ? в) ; В .
Яка з умов гарантує збіжність ряду ? г) - неперервна, спадна, ;.
Яка з умов гарантує збіжність ряду ? г) ; Г .
Яка з умов гарантує розбіжність ряду ? б) ; Б .
Яка з
умов гарантує розбіжність ряду
?
а)
![]() ;
А .
;
А .
Яка з
умов гарантує розбіжність ряду
?
в)
![]() ;
В .
;
В .
Яка з умов гарантує розбіжність ряду ? г) ;
Яка з
формул для обчислення площі області
,
обмеженої контуром
не є
правильною
? а)![]() ;
А .
;
А .
Яка функція є сумою ряду ? б) ; Б .
Яка функція є сумою ряду ? в) ; В .
Яка функція є сумою ряду ? а) ; А .
Яка функція є сумою ряду ? в) ; В .
Яка
функція є сумою ряду
![]() ? а)
;
А .
? а)
;
А .
Яка функція є сумою ряду ? г) ; Г .
Яка
функція є сумою ряду
![]() ? б)
;
Б .
? б)
;
Б .
Яка
функція є сумою ряду
![]() ? в)
;
В .
? в)
;
В .
Яка
функція є сумою ряду
![]() ? г)
;
Г .
? г)
;
Г .
Які з
наведених нижче рівностей вірні
:
2)
![]() ;
3)
;
3)![]() ;
г) 2 і 3; Г
.
;
г) 2 і 3; Г
.
Які з
наведених нижче рівностей вірні
:1)
![]() ;
3)
;
3)![]() ;
б) 1 і 3;
Б .
;
б) 1 і 3;
Б .
Які з
наведених нижче рівностей є правильними
(
,
)
1)![]() ;4)
;4)
![]() .
г)
1 і 4; Г.
.
г)
1 і 4; Г.
Які з
наведених нижче рівностей є правильними
(
,
)?
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
д) інша відповідь.
.
д) інша відповідь.
Які з
наведених нижче рівностей є правильними
(
,
)?
1)![]() ;
3)
;
3)
![]() ;
б) 1 і 3; Б .
;
б) 1 і 3; Б .
Які з
наведених нижче рівностей справедливі
для криволінійного інтеграла
першого
роду ?1)
![]() ;2)
;2)
![]() ;
3)
;
3)
![]() ;4)
;4)
![]() .г)
1 і 4;
Г .
.г)
1 і 4;
Г .
Які з
наведених нижче рівностей справедливі
для криволінійного інтеграла
першого
роду ?1)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
б) 2 і 3;
Б .
;
б) 2 і 3;
Б .
Які з
наведених нижче рівностей справедливі
для криволінійного інтеграла
другого
роду? 1)![]() (
(![]() )
2)
)
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
д)
інша відповідь. Д .
.
д)
інша відповідь. Д .
Які з
наведених нижче рівностей справедливі
для подвійного інтеграла ?1)
![]() ;2)
;2)
![]() ;3)
;3)
![]() ;4)
;4)
![]() (
).г) 3 і 4;
Г
.
(
).г) 3 і 4;
Г
.
Які з
наведених нижче рівностей справедливі
для потрійного інтеграла?1)
![]() ;2)
;2)
![]() ;3)
;3)
 ;
4)
;
4)
![]() .в)
1 і 4; В .
.в)
1 і 4; В .
Які з наведених нижче тверджень є правильними? 1)Обмеженість функції в обмеженій замкненій області є достатньою умовою її інтегровності в цій області. 2).Неперервність функції в обмеженій замкненій області є достатньою умовою її інтегровності в цій області.3)Обмеженість функції в обмеженій замкненій області є необхідною умовою її інтегровності в цій області.4)Неперервність функції в обмеженій замкненій області є необхідною умовою її інтегровності в цій області.б) 2 і 3; Б .
Які з наведених нижче тверджень є правильними?1)Якщо функція інтегровна в області , то вона неперервна в цій області.2)Якщо функція інтегровна в обмеженій замкненій області , то вона обмежена в цій області. 3)Для того, щоб функція була інтегровною в області необхідно і достатньо, щоб область була обмеженою і замкненою, а функція – обмеженою в цій області.4)Якщо функція неперервна в обмеженій замкненій області , то вона інтегровна в цій області. в) 2 і 4; В .
Які з наведених нижче тверджень не є правильними ?1) Для того, щоб функція була інтегровною в області необхідно, щоб вона була неперервною в цій області.2) Для того, щоб функція була інтегровною в області необхідно, щоб вона була обмеженою в цій області.3) Для того, щоб функція була інтегровною в області достатньо, щоб вона була обмеженою в цій області.4) Для того, щоб функція була інтегровною в області достатньо, щоб область була обмеженою і замкненою, а функція була неперервною в цій області.в) 1 і 3; В .
Які з наведених нижче тверджень не є правильними ?1)Для того, щоб функція була інтегровною в обмеженій замкненій області необхідно і достатньо, щоб функція була неперервною в цій області.2)Для того, щоб функція була інтегровною в обмеженій замкненій області необхідно, щоб функція була обмеженою в цій області.3)Для того, щоб функція була інтегровною в обмеженій замкненій області достатньо, щоб вона була неперервною в цій області.4)Для того, щоб функція була інтегровною в обмеженій замкненій області достатньо, щоб вона була обмеженою в цій області.а) 1 і 4; А .
Які з
наведених нижче тверджень неправильні?
2) Якщо ряд
розбіжний, то ряд
![]() може збігатись. 3) Якщо ряд
збіжний, то ряд
може розбігатись. б) 2 і 3; . Б .
може збігатись. 3) Якщо ряд
збіжний, то ряд
може розбігатись. б) 2 і 3; . Б .
Які з наведених нижче тверджень правильні? 1) Якщо ряд збіжний, то ряд теж збіжний. 3) Якщо ряд розбіжний, то ряд може збігатись. в) 1 і 3; В .
Які з
наведених нижче тверджень справедливі
для подвійного інтеграла ?1)Якщо
в області
функція
![]() ,
то
,
то
![]() ;2)Якщо
область
;2)Якщо
область
![]() ,
причому
,
причому
![]() і
і
![]() не мають спільних внутрішніх точок, то
не мають спільних внутрішніх точок, то
![]() ;3)Для
довільних обмежених замкнених областей
і
справедлива рівність
;3)Для
довільних обмежених замкнених областей
і
справедлива рівність
![]() ;4)
;4)![]() ,
де
- площа області
.в)
1 і 2; В .
,
де
- площа області
.в)
1 і 2; В .
Які з
наведених нижче формул є правильними
? 1) (
- проекція
на площину
(
- проекція
на площину
![]() );2)
);2)
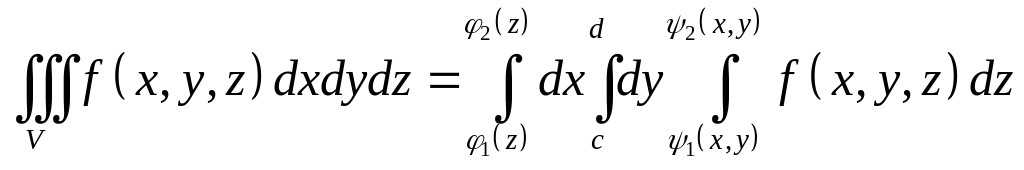 ;
3)
;
3)
 ;4)
;4)
 (
- проекція
на
площину
(
- проекція
на
площину
![]() ).в)
1 і 3; В .
).в)
1 і 3; В .
Які з
наведених нижче формул є правильними
?1)
 (
- проекція
на площину
(
- проекція
на площину
![]() );2)
);2)
 ;3)
;3)
 ;4)
;4)
 (
- проекція
на площину
).д)
інша відповідь. Д .
(
- проекція
на площину
).д)
інша відповідь. Д .
Які з
наведених нижче формул є правильними
?1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .г)
тільки 4;
Г .
.г)
тільки 4;
Г .
Які з
наведених нижче формул є правильними
?1)
 ;
2)
;3)
;
2)
;3)
 ;
4)
.д)
інша відповідь.
;
4)
.д)
інша відповідь.
Які з
наведених нижче формул є правильними
?1)
;2)
 ;3)
;
4)
.в)
2 і 3; В .
;3)
;
4)
.в)
2 і 3; В .
Які з
наведених нижче формул не можуть бути
правильними ?1)
 ;
2)
;
2)
 ;3)
;
4)
.д)
інша відповідь.
;3)
;
4)
.д)
інша відповідь.
Які з
наведених нижче формул не можуть бути
правильними ?1)
 ;
2)
;
2)
 ;3)
;3)
 ;
4)
.а)
1, 2 і 3; А
;
4)
.а)
1, 2 і 3; А
Які з
наведених нижче формул не можуть бути
правильними ?1)
 ;2)
;2)
 ;3)
;3)
 ;4)
;4)
 .
б) 2 і 4; Б .
.
б) 2 і 4; Б .
Які з
наведених нижче формул не можуть бути
правильними ?1)
 ;2)
;2)
 ;3)
;3)
 ;4)
;4)
 .г)
2 і 3;
Г .
.г)
2 і 3;
Г .
Якщо
-
замкнений контур, всередині якого
знаходиться одна особлива точка
функції
,
то справедлива рівність: б)
![]() ;
Б
.
;
Б
.
Якщо
-
замкнений контур, всередині якого
знаходиться одна особлива точка
функції
,
то: 2)
![]() ;
4)
;
4)
![]() .
в) 2 і 4;
В .
.
в) 2 і 4;
В .
Якщо
і
![]() - відповідно найменше і найбільше
значення функції
в області
,
а
- площа цієї області, то має місце оцінка
подвійного інтеграла:б)
- відповідно найменше і найбільше
значення функції
в області
,
а
- площа цієї області, то має місце оцінка
подвійного інтеграла:б)
![]() ;Б
.
;Б
.
Якщо
для двох рядів
і
виконується
![]() для всіх
для всіх
![]() ,
то:
б) із збіжності ряду
випливає збіжність ряду
,
то:
б) із збіжності ряду
випливає збіжність ряду
Якщо для двох рядів і виконується для всіх , то: в) із розбіжності ряду випливає розбіжність ряду ; В .
Якщо
існує таке
![]() ,
що для всіх членів послідовності
,
що для всіх членів послідовності
![]() ,
то така послідовність називається: б)
обмеженою; Б
.
,
то така послідовність називається: б)
обмеженою; Б
.
Якщо
крива
задана параметричними рівняннями
![]() ,
то
для обчислення криволінійного інтеграла
першого роду має місце формула:г)
,
то
для обчислення криволінійного інтеграла
першого роду має місце формула:г)
 ;
;
Якщо
крива
задана параметричними рівняннями
![]() ,
то
для обчислення криволінійного інтеграла
другого роду має місце формула: а)
,
то
для обчислення криволінійного інтеграла
другого роду має місце формула: а)![]() ;
А
.
;
А
.
Якщо
крива
задана рівнянням
![]() ,
то для обчислення
криволінійного
інтеграла першого роду має місце
формула:а)
,
то для обчислення
криволінійного
інтеграла першого роду має місце
формула:а)
![]() ;
А .
;
А .
Якщо
крива
задана рівнянням
![]() ,
то для обчислення
криволінійного
інтеграла першого роду має місце
формула:в)
,
то для обчислення
криволінійного
інтеграла першого роду має місце
формула:в)
![]() ;
В .
;
В .
Якщо
крива
задана рівнянням
,
то для обчислення
криволінійного
інтеграла другого роду має місце формула:
б)
![]() ;
Б .
;
Б .
Якщо
крива
задана рівнянням
,
то для обчислення
криволінійного
інтеграла другого роду має місце формула:
г)
![]() ;
Г .
;
Г .
Якщо
поверхня
задана рівнянням
![]() і проектується на площину
в
область
,
то її площа
знаходиться за формулою: в)
і проектується на площину
в
область
,
то її площа
знаходиться за формулою: в)![]() ;
В .
;
В .
Якщо
поверхня
задана рівнянням
![]() і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: в)
і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: в)![]() ;
В
.
;
В
.
Якщо
поверхня
задана рівнянням
![]() і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: а)
і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: а)![]() ;
А
.
;
А
.
Якщо
поверхня
задана рівнянням
![]() і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: б)
і проектується на площину
в
область
,
то для обчислення поверхневого інтеграла
першого роду має
місце
формула: б)![]() ;
Б .
;
Б .
Якщо
просторова крива
задана параметричними рівняннями
![]()
![]() ,
то для обчислення криволінійного
інтеграла
першого
роду має місце формула:а)
,
то для обчислення криволінійного
інтеграла
першого
роду має місце формула:а)
 ;А
.
;А
.
Якщо ряд збіжний, то: б) ; Б .
Якщо
функція
аналітична в області
,
обмеженій контуром
і на самому контурі, то для
![]() :
Із наведених рівностей вірними є:
д) інша відповідь. Д
.
:
Із наведених рівностей вірними є:
д) інша відповідь. Д
.
Якщо
функція
аналітична на дійсній осі, а також у
всій комплексній площині за винятком
скінченного числа ізольованих особливих
точок і при деякому
![]() для
для
![]() таких, що
таких, що
![]() ,
де
і
-
додатні константи, причому
,
де
і
-
додатні константи, причому
![]() ,
то
,
то
![]() ,
де
,
де
![]() -
особливі точки функції
розташовані: б) у верхній півплощині;
Б
.
-
особливі точки функції
розташовані: б) у верхній півплощині;
Б
.
Якщо
функція
аналітична на межі
однозв’язної області
і в самій області
за винятком ізольованих особливих точок
,
то: г)![]() ;
Г
.
;
Г
.
Якщо
функція
аналітична у верхній півплощині,
включаючи дійсну вісь, за винятком
скінченного числа особливих точок
і
![]() рівномірно відносно
рівномірно відносно
![]() ,
то: а)
,
то: а)
![]() ;
А
.
;
А
.
