Вычисление резервного времени

Резервное время простоя можно вычислить двумя способами:

Резервное время = LS – ES или LF – EF

Используя этот вычислительный алгоритм, критический путь обозначают действиями с нулевым резервом времени. Так, таблица в примере 4 показывает, что действия 1-2, 2-5 и 5-6 все являются критическими, что соответствует результатам в примере 1, которые были получены интуитивным методом.

Резерв времени — допустимый простой для пути; разница между длиной данного пути и длиной критического пути.

Знание показателей резервного времени позволяет менеджеру точнее спланировать распределение ограниченных ресурсов и направить деятельность по контролю нa те действия, которые могут вызвать задержку в завершении проекта в срок. При этом точность решений будет выше, чем при более упрощенном интуитивном подходе. В этом отношении, важно помнить, что резервное время действия основано на предпосылке, что все действия на этом пути будут начаты как можно раньше и не превысят своей плановой продолжительности. Кроме того, если два действия на одном пути (например, действия 2-4 и 4-5 в предыдущем примере) имеют одинаковый резерв времени (например, две недели), этот показатель будет обозначать общее (суммарное) резервное время обоих действий. В сущности, действия на пути имеют общий временной резерв. Следовательно, если первое действие использует весь резерв, для другого действия резерв будет нулевым. Настолько же уменьшится резерв и для всех остальных действий на этом пути.

ПРИМЕР 3.4

Рассчитайте резервное время для сетевой диаграммы, приведенной в описании к примеру 3.2.

Решение:

Вы можете использовать показатели начального времени или конечного времени. Предположим, мы выбираем начальное время. Используя время ES, вычисленное в примере 2, и время LS, вычисленное в примере 3, резервное время будет следующим:

Действие	LS	ES	(LS – ES) Резерв времени
1-2	0	0	0
1-3	6	0	6
2-4	10	8	2
2-5	8	8	0
3-5	10	4	6
4-5	16	14	2
5-6	19	19	0

Как отмечено выше, данный алгоритм поддается компьютеризации.

3.4. Вероятностные оценки времени

Все сказанное выше основывалось на предпосылке, что время действий известно и не подвержено изменениям. Во многих ситуациях данная предпосылка приемлема, однако существует много других ситуаций, где она не действует. Соответственно, эти ситуации требуют вероятностного подхода.

Вероятностный подход требует для каждого действия трех временных оценок вместо одной:

1. Оптимистическое время — время действия при оптимальных условиях.

   Оптимистическое время: время действия при оптимальных условиях; обозначается символом о.

2. Пессимистическое время: время действия при наихудших условиях; обозначается символом p.

3. Наиболее вероятное время: наиболее вероятное время действия; обозначается символом т.

Пессимистическое время — время действия при худших возможных условиях

Эти временные оценки могут быть сделаны руководителем проекта или другими сотрудниками, хорошо знакомыми с проектом.

Наиболее вероятное время — наиболее вepoятное время действия.

Как правило, для описания отклонений, присущих временным параметрам, используют бета-распределение (рис. 3.4). Хотя нет никаких реальных теоретических предпосылок для использования бета-распределения, некоторые особенности делают его очень удобным для применения на практике: распределение может быть симметричным или смещенным вправо или влево, в зависимости от характера данного действия; среднее значение и дисперсию распределения можно легко получить из трех временных оценок, перечисленных выше; распределение является унимодальным с высокой концентрацией вероятности вокруг наиболее вероятной временной оценки.

Рис. 3.4. Бета-распределение. Используется для описания вероятностных временных оценок

Особый интерес для сетевого анализа представляет среднее или ожидаемое время для каждого действия t_e а также дисперсия времени каждого действия. Ожидаемое время вычисляется как взвешенное среднее трех временных оценок.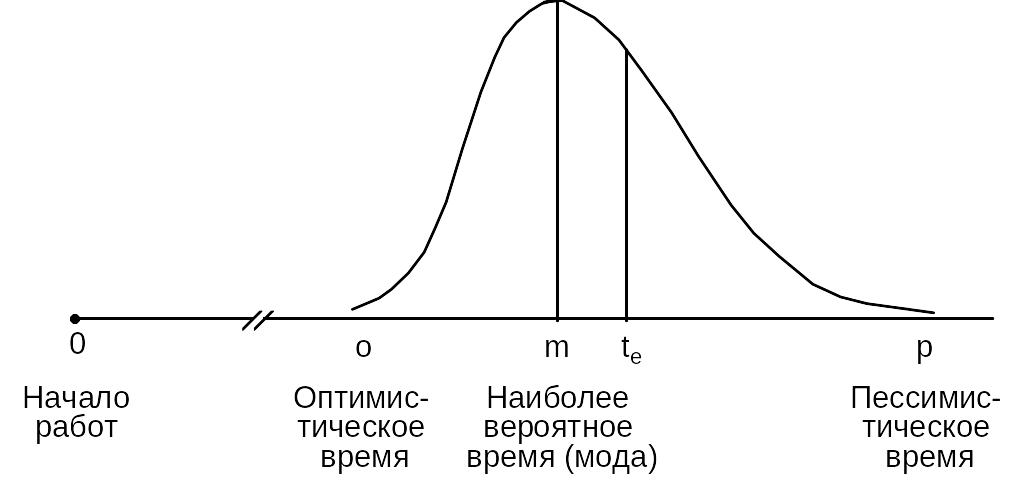

Стандартное отклонение  времени каждого действия оценивается в одну шестую разницы между пессимистической и оптимистической оценкой времени. (Аналогично, практически вся область под кривой нормального распределения находится в пределах трех стандартных отклонений от среднего, т.е. в диапазоне шести стандартных отклонений.) Отклонение (дисперсия) вычисляется как квадрат стандартного отклонения:

^ или

Величина дисперсии отражает степень неопределенности, связанной со временем действия: чем больше дисперсия, тем больше неопределенность (неуверенность).

Желательно также рассчитать стандартное отклонение ожидаемого времени для каждого пути. Это можно сделать, сложив показатели дисперсии действий на пути и затем извлечь квадратный корень из этого числа; то есть:

_пути

Знание ожидаемых показателей времени на пути и их стандартного отклонения позволяет менеджеру рассчитать вероятностные оценки времени завершения проекта, такие как:

• Вероятность, что проект будет завершен в установленный срок.

• Вероятность, что для завершения проекта потребуется больше времени, чем предусмотрено планом.

Оценки данного типа основаны на предпосылке, что продолжительность времени пути — случайная переменная, которая нормально распределяется вокруг ожидаемого времени пути. Использование нормального распределения обосновано тем, что мы суммируем время действий (случайные переменные), а суммы случайных переменных обычно нормально распределены, когда число суммируемых элементов велико. Однако даже в том случае, когда число слагаемых относительно мало, нормальное распределение дает приемлемое приближение к фактическому распределению.

Следующий пример показывает, как нормальное распределение используется для определения вероятности различных сроков завершения. Прежде, чем мы рассмотрим этот пример, важно обратить внимание на два момента. Один касается независимости показателей времени пути друг от друга. В сущности, это требует соблюдения двух условий: независимости временных показателей друг от друга, и чтобы каждое действие размещалось только на одном пути. Для того, чтобы времена действий были независимыми, необходимо, чтобы ни одно не было функцией другого. Если времена двух действий всегда изменяются одинаково (например, всегда одинаково запаздывают), то эти действия не могут считаться независимыми. Второй важный момент заключается в том, что проект не будет завершен, пока не завершатся все его действия, — а не только те, что находятся на критическом пути. Иногда бывает так, что какой-то другой путь требует большего количества времени, чем критический путь. В этом случае проект выполняется дольше, чем планировалось. Следовательно, рискованно сосредоточиваться исключительно на критическом пути. Вместо этого, необходимо учитывать возможность, что по крайней мере один какой-то путь задержит своевременное завершение проекта. Это требует определения вероятности, что все пути «финишируют» в срок. Для этого рассчитайте вероятность того, что каждый путь закончится своевременно, и перемножьте полученные результаты. Обратите внимание: следует рассматривать только пути, относительно близкие к критическому по своим временным показателям. Маловероятно, что путь с ожидаемым временем намного меньше критического, превысит время критического пути. Существует простое эмпирическое правило: считать вероятность своевременного завершения пути за 100%, если его ожидаемое время плюс 2,5 его стандартного отклонения — меньше, чем заданное время. Эти положения иллюстрируются в примере 6.

ПРИМЕР 3.5

Сетевая диаграмма для проекта показана ниже. Даны три временных оценки для каждого действия. Время действий задано в месяцах. Сделайте следующее:

1. Рассчитайте ожидаемое время каждого действия и ожидаемую продолжительность каждого пути.

1. Определите критический путь.

1. Рассчитайте дисперсию каждого действия и дисперсию каждого пути.

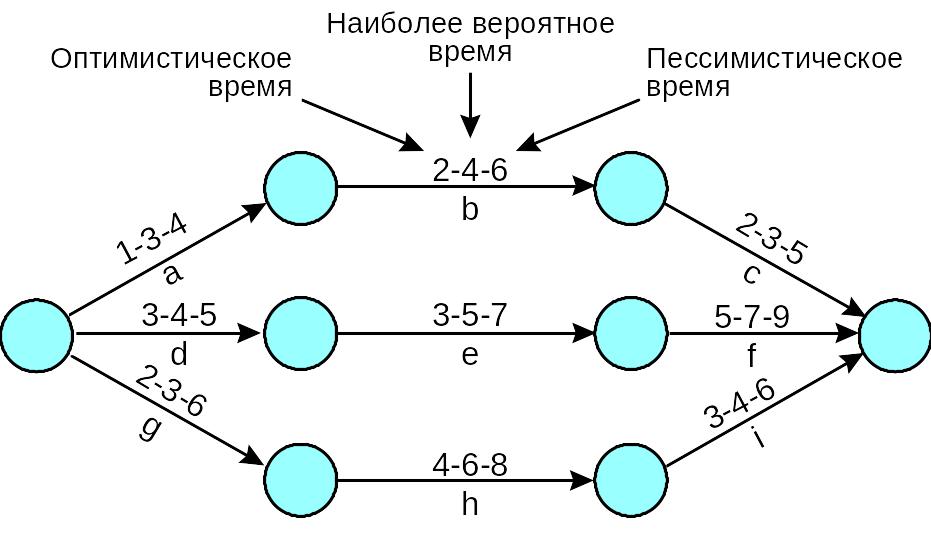
Решение:

Путь	Действие		Время		t=(o+4m+p)/6	Общее время
		о	т	p		пути
а-b-с	а	1	3	4	2,83	10,00
	b	2	4	6	4,00
	с	2	3	5	3,17
d-e-f	d	3	4	5	4,00	16,00
	е	3	5	7	5,00
	f	5	7	9	7,00
g-h-i	g	2	3	6	3,33	13,50
	h	4	6	8	6,00
	i	3	4	6	4,17

1. Путь, у которого самая большая ожидаемая продолжительность, — это критический путь. Так как путь d-e-f имеет самое большое общее время, он и является критическим.

		Время
Путь	Действие	о	m	p	2действ = (p – o)2 / 36	2пути	пути
а-b-с	а	1	3	4	(4 – 1)2 / 36 = 9/36	34/36=0,944	0,97
	b	2	4	6	(6 – 2)2 / З6 = 1б/З6
	с	2	3	5	(5 – 2)2 / 36 = 9/36
d-e-f	d	3	4	5	(5 – З)2 / 36 = 4/36	36/36=1,00	1,00
	е	3	5	7	(7 – 3)2 / 36 = 16/36
	f	5	7	9	(9 – 5)2 / З6 = 1б/З6
g-h-i	g	2	3	6	(6 – 2)2 / 36 = 16/36	41/36=1,139	1,07
	h	4	6	8	(8 – 4)2 / 36 = 16/36
	i	3	4	6	(6 – З)2 / З6 = 9/36

ПРИМЕР 3.6

Используя информацию из примера 5, ответьте на следующие вопросы:

1. Могут ли пути считаться независимыми? Почему?

1. Какова вероятность, что проект будет завершен в пределах 17 месяцев от начала?

1. Какова вероятность, что проект будет завершен в пределах 15 месяцев от начала?

1. Какова вероятность, что проект не будет завершен в пределах 15 месяцев от начала?

Решение:

1. Да, пути могут считаться независимыми, так как ни одно действие не находится более чем на одном пути, и у нас нет никакой информации о том, что времена каких-либо действий связаны.

1. Чтобы отвечать на вопросы такого типа, надо принять во внимание, в какой степени распределения пути «накладываются» на заданное время завершения проекта. Это положение проиллюстрировано на приведенном ниже рисунке, который показывает три распределения пути. Каждое распределение центрировано на ожидаемой продолжительности этого пути, и относительно определенного времени завершения —17 месяцев.

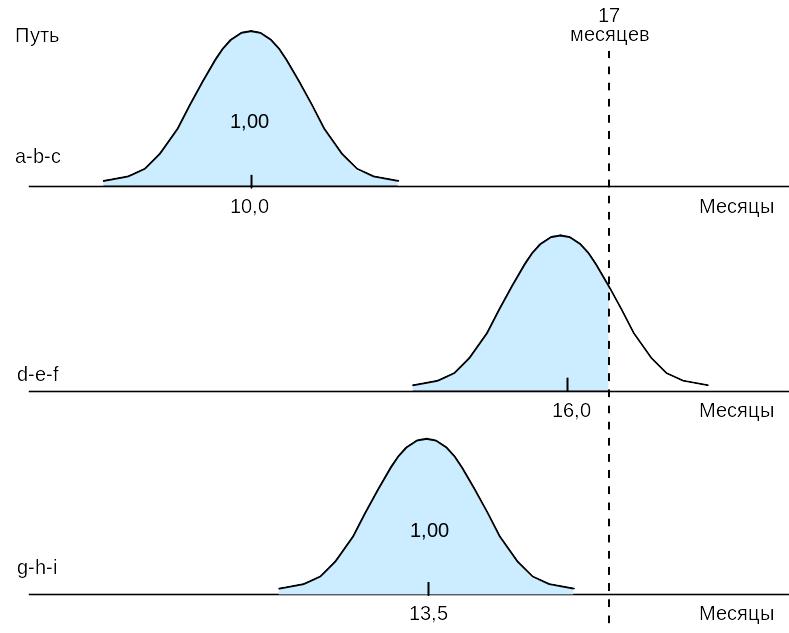
Левая часть каждого распределения соответствует вероятности, что эта часть будет завершена в пределах заданного времени. Обратите внимание, что пути а-b-с и g-h-i значительно смещены влево от заданного времени, поэтому очень высока вероятность, что оба они будут закончены к месяцу 17. Однако критический путь накладывается на заданное время завершения. Следовательно, оценивая вероятность завершения проекта к месяцу 17, нам надо принимать во внимание только распределение пути d-e-f. Для этого нужно сначала вычислить значение z, используя следующее соотношение:

(1)

В данном случае,

Обратившись к табл. А в приложении для z = +1,00, вы увидите, что область под кривой слева от z будет равна 0,8413. Следовательно, вероятность завершения проекта в пределах 17 месяцев от начала равна 0,8413.

1. Этот вопрос показывает, как обрабатывать задачу, в которой более чем одно распределение перекрывает заданное время. На приведенном ниже рисунке, обратите внимание, что пути d-e-f и g-h-i накладываются на месяц 15. Это означает что оба пути потенциально могут задержать проект — т.е. проект не уложится в 15 месяцев.

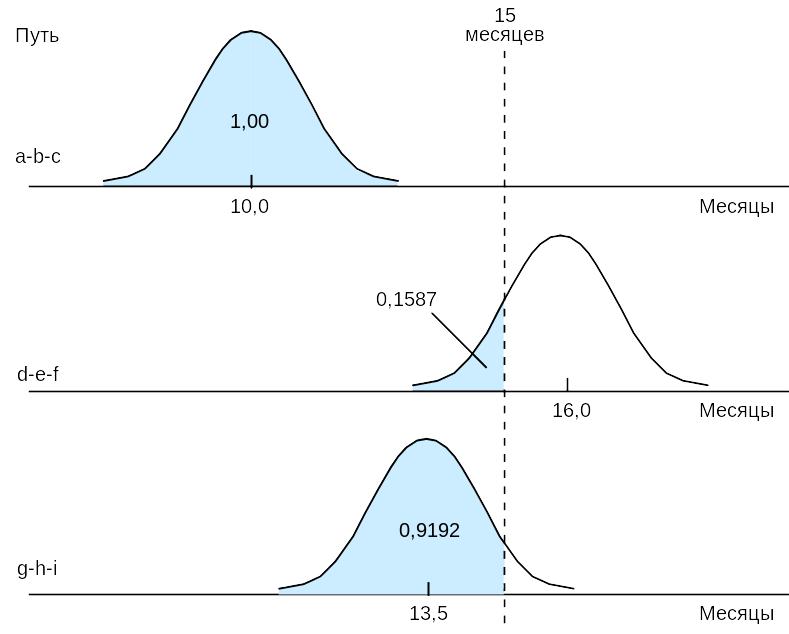
Хотя рисунок полезен для наглядного представления концепции накладывающихся путей, но все же необходим более строгий подход, чтобы определить, какие пути рассматривать, и чему равна вероятность завершения каждого пути в срок. Для этого требуется рассчитать значение z для каждого пути, используя формулу (1). Тогда считается, что любой путь со значением z больше чем +2,50, имеет вероятность завершения 100%. Для других определяется совокупная вероятность завершения в срок. Для нашей задачи, с заданным временем 15 месяцев, значения z таковы:

Путь		Вероятность завершения в пределах 15 месяцев
а-b-с d-e-f g-h-i	(15 – 10,0) / 0,97 = +5,15 (15 – 16,0) / 1,00 = –1,00 (15 – 13,5) / 1,07 = +1,40	1,0000 0,1587 0,9192

В табл. В из приложения, область слева от z = –1,00 будет 0,1587, а область слева от z = +1,40 будет 0,9192. Общая вероятность завершения этих путей за 15 месяцев является произведением их вероятностей:

1,00  (0,1587)  (0,9192) = 0,1459.