Система обозначений сетевых диаграмм

Построение и интерпретация сетевых диаграмм требует некоторого знакомства с системой обозначений сетевых диаграмм. Хотя их достаточно много, мы обсудим только некоторые самые важные и самые широкоупотребительные параметры сетевых диаграмм. Этого будет достаточно, чтобы дать вам основу для понимания основных положений, связанных с диаграммами предшествования, и позволит решать типичные задачи.

Одна из основных особенностей диаграммы предшествования — то, что она показывает, какие действия должны выполняться последовательно (т.е. соблюдается условие предшествования), а какие можно выполнять независимо друг от друга. Например, в приведенной ниже диаграмме, действие А должно быть завершено прежде, чем начнется действие В, и действие В должно быть завершено прежде, чем можно будет начать действие С.

Если диаграмма выглядит так, как показано ниже, оба действия А и В должны завершиться прежде, чем начнется действие С, но А и В могут выполняться одновременно; выполнение А не зависит от выполнения В.

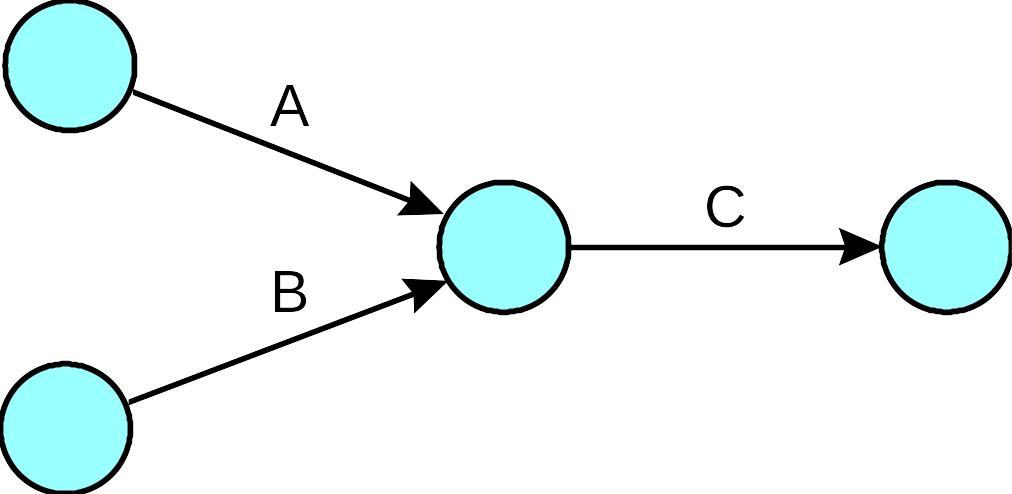
Если действие А должно предшествовать В и С, то соответствующая сетевая диаграмма будет выглядеть следующим образом:

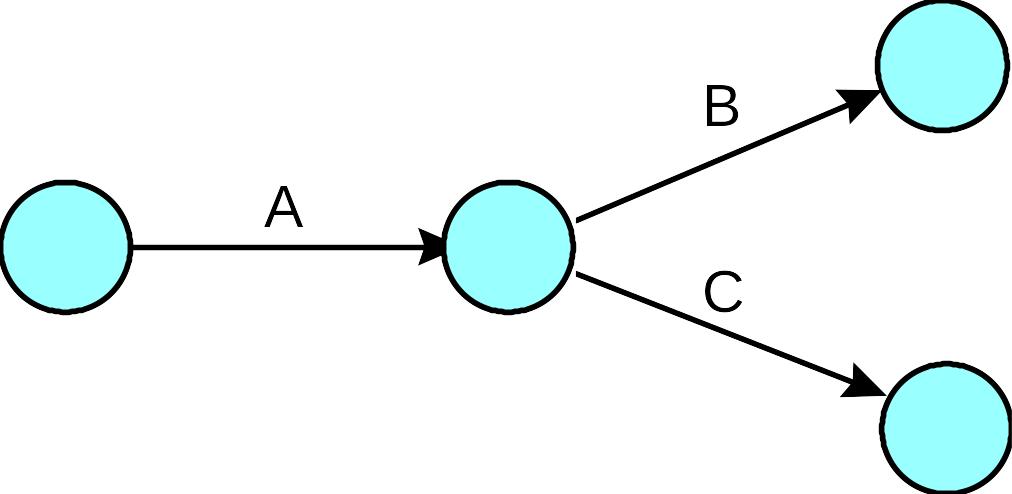
Когда в узловую точку входят несколько действий, то это значит, что все эти действия должны завершиться прежде, чем начнутся любые действия, которые начинаются в данном узле. Следовательно, в приведенной ниже диаграмме, действия А и В необходимо закончить прежде, чем можно будет начать действия С или D.

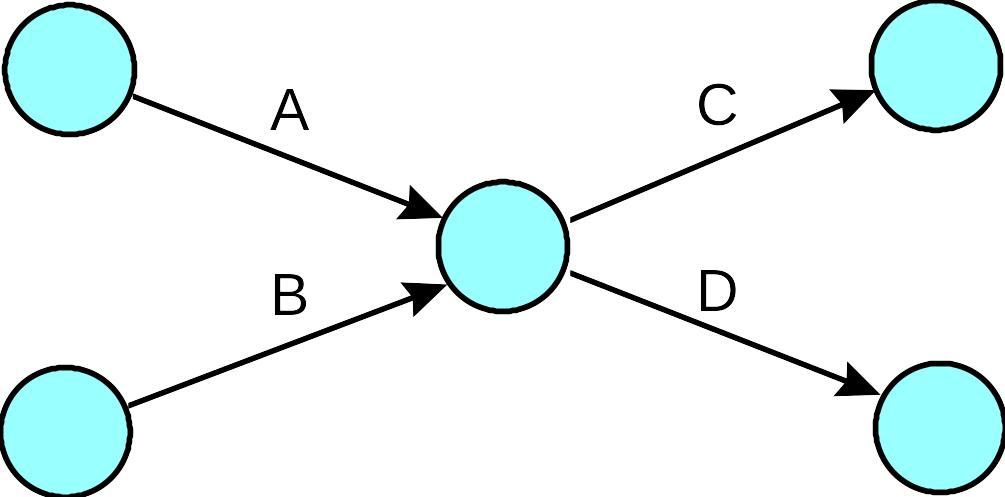
Когда два действия имеют одни и те же начальные и конечные узлы, используются фиктивный узел и действие, чтобы сохранить тождество каждого действия. В диаграмме, показанной ниже, действия А и В должны быть завершены прежде, чем будет начато действие С.

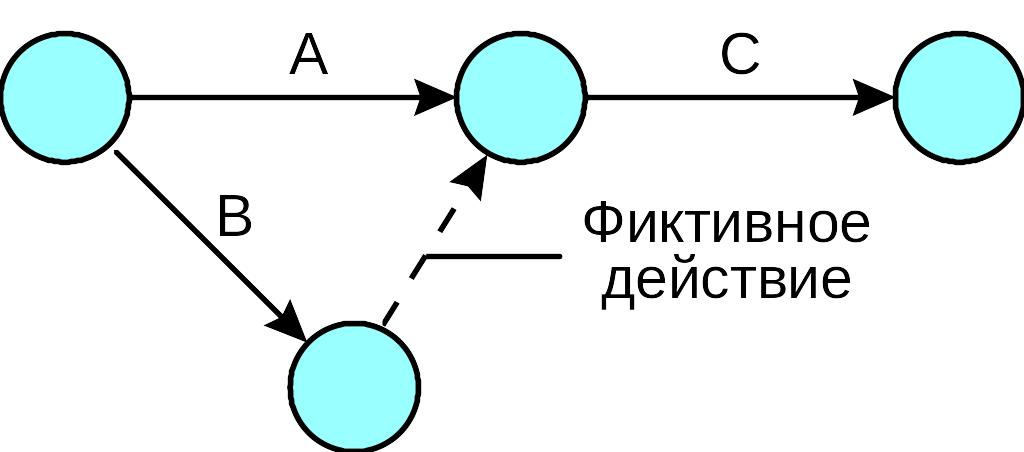
Тождества действий особенно важны для компьютерного анализа, потому что большинство компьютерных программ идентифицируют действия по их конечным точкам; действия с одними и теми же конечными точками могут быть неразличимы друг от друга, хотя они и имеют совершенно разные временные показатели.

Фиктивные действия можно использовать различными способами. Еще один такой способ показан ниже:

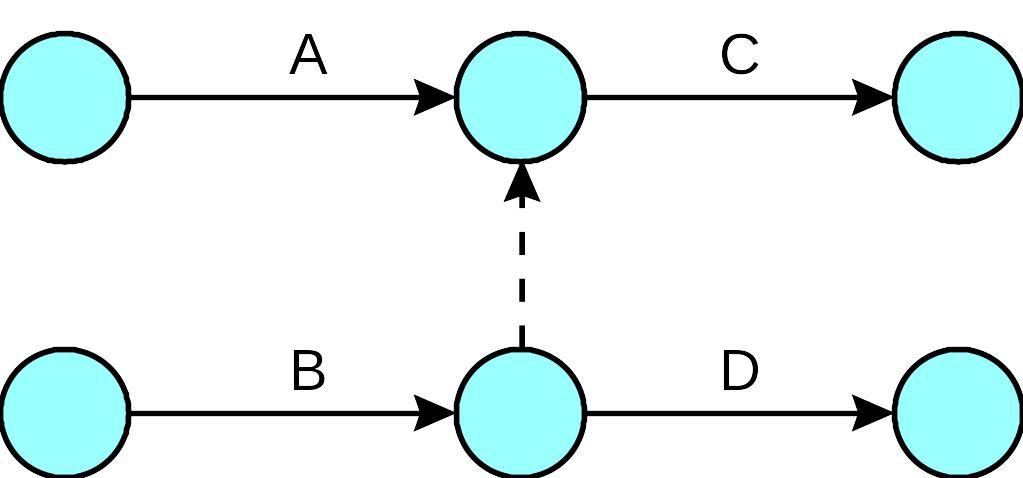
В данной ситуации действия А и В, оба должны предшествовать действию С. Однако начало действия D зависит только от выполнения действия В и не зависит от выполнения А.

Основная функция фиктивного действия - прояснять взаимосвязи. В том, что касается времени, фиктивное действие имеет нулевой показатель.

Для последующих ссылок, узловые точки нумеруются слева направо. Иногда в процессе построения сетевой диаграммы, для большей наглядности, используются стрелки, обозначающие начало и конец.

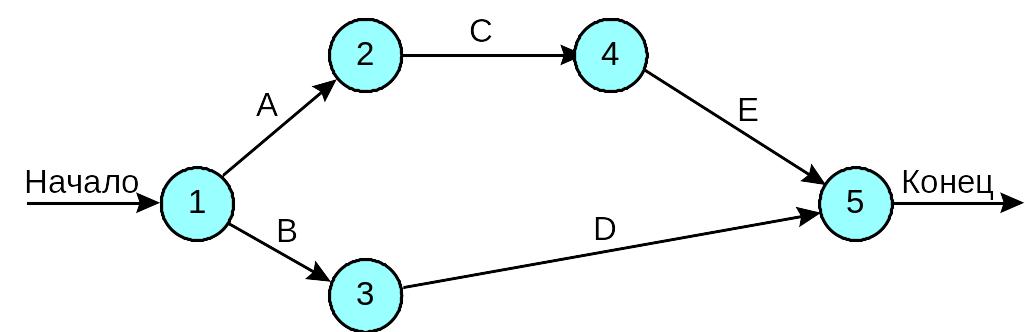
3.3. Детерминированные показатели времени

Детерминированный показатель — оценка времени, сделанная с достаточной точностью.

Вероятностный показатель — оценка времени, поверженная изменениям

Существует основной фактор, которым определяет, как будет применен метод сетевых диаграмм для анализа и интерпретации сетей. Этот фактор — детерминированные или вероятностные показатели времени (оценки времени). Если можно определить временные показатели с высокой степенью уверенности, что они не будут сильно отличаться от реальных, то говорят, что оценка детерминированная. Если оценка времени может измениться, то говорят, что оценка вероятностная. Вероятностная оценка должна включать показатель вероятного отклонения.

В данном разделе описан анализ сетевых диаграмм с детерминированными оценками времени. Позже мы расскажем о вероятностной оценке.

ПРИМЕР 3.1

Дана следующая информация

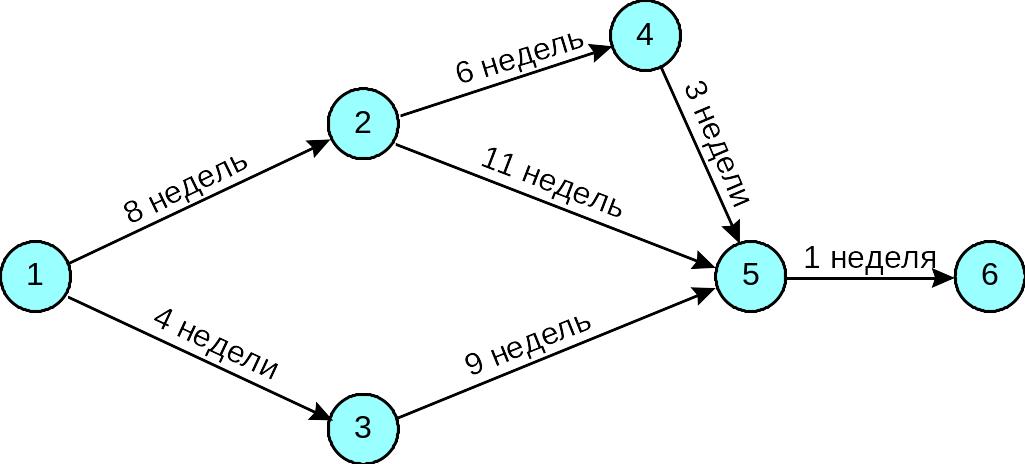
Определите:

1. Длину каждого пути.

1. Критический путь.

1. Ожидаемую продолжительность проекта.

1. Количество резервного времени для каждого пути.

Решение:

1. Как показано в следующей таблице, длина путей — 18 недель, 20 недель и 14 недель.

1. Самый длинный путь (20 недель) — 1-2-5-6, поэтому он является критическим путем.

1. Ожидаемая продолжительность проекта равна длине критического пути (т.е. 20 недель).

1. Мы находим резерв времени для каждого пути, вычитая длину этого пути из длины критического пути, как это показано в последнем столбце таблицы. (Обратите внимание: иногда желательно знать резервное время для каждого действия. Следующий раздел описывает метод получения таких показателей.)

Путь	Длина пути (недели)	Резервное время
1-2-4-5-6 1-2-5-6 1-3-5-6	8 + 6 + 3 + 1 = 18 8 + 11 + 1 = 20 * 4 + 9 + 1 = 14	20 – 18 = 2 20 – 20 = 0 20 – 14 = 6
*Длина критического пути

Сетевые диаграммы многих реальных проектов намного больше, чем простая сеть, показанная в предшествующем примере; они часто содержат сотни и даже тысячи действий. Поскольку необходимые вычисления могут стать чрезвычайно сложными и потребовать много времени, большие сетевые диаграммы, как правило, анализируются компьютерными программами, а не вручную. Интуитивный подход, показанный выше, не поддается компьютеризации, потому что во многих случаях последовательности путей не так легко распознать. Вместо этого, используют алгоритм для получения четырех видов информации о действиях в сети [9, с. 16]:

ES — самое раннее время, когда действие может начаться при условии, что все предшествующие действия начинаются как можно раньше.

EF — самое раннее время, когда действие может быть законченно.

LS — самое позднее время, когда действие может начаться, не задерживая проект.

LF — самое позднее время, когда действие может закончиться, не задерживая проект.

Когда эти значения определены, их можно использовать, чтобы найти:

1. ожидаемую продолжительность проекта;

2. резервное время;

3. действия на критическом пути.