1 Розрахунок статичного режиму ключа методом Ньютона.

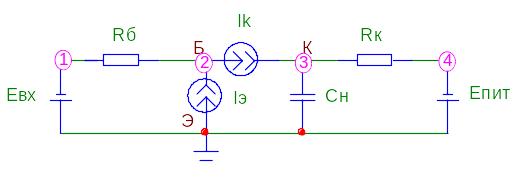
1. Побудуємо схему заміщення ключа (рисунок Є.5.1).

Рисунок Є.5.3 – Спрощена Рисунок є5.4 – Схема заміщення ключа для

модель для БТ pnp-типу розрахунку статики

Рисунок Є.5.1 – Схема транзисторного ключа

Рисунок Є.5.2 – Модель Еберса-Молла

Для біполярного транзистора використана спрощена схема заміщення, отримана з моделі Еберса-Молла (рисунок Є.5.2).

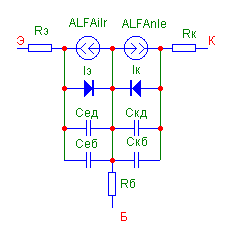
Оскільки аналізується статика, ємностями колектора і емітера моделі Еберса-Молла можна знехтувати. Нехтуємо опором утікання та елементами, що моделюють інверсний режим. Для спрощення обчислень нехтуємо об’ємними опорами бази, емітера і колектора. Для аналізу статичного режиму відкидаємо ємність Сн, оскільки її опір постійному струму нескінчений.

Спрощена модель наведена на рисунку Є.3. Підставляючи її в схему Є.1, отримуємо модель ключа (рисунок 4).

2. Отримаємо рівняння математичної моделі ключа.

Стани четвертого и першого вузлів визначені (вони задаються джерелами), складаємо рівняння по першому закону Кірхгофа для вузлів 2 та 3:

2: I_rб+ Jэ- Jк=0

3: Jк- I_сбн + I_rк=0

Система буде нелінійною, оскільки БТ – нелінійний компонент.

Її можна записати в виді:

I_rб+Jэ–_N*Jэ = 0

_N*Jэ -I_сбн + I_rк = 0

де

Jэ= Іэ₀*(е^uэ/mt-1)=Іэ₀*(е^u2/mt-1);

Jк=_N* Іэ₀*(е^uэ/mt-1) = _N* Іэ₀*(е ^{u2 /mt}-1);

I_сн=Cн*dU_cн/dt =Cн*(d U3/ dt) ;

Виразимо струми I_rб и I_rк через напруги::

2: (U2-Eвх)/R_б+(1–_N) Іэ₀*(е^u2/mt-1) = 0

3: _N* Іэ₀*(е^u2/mt-1) – Cн*(d U3/ dt) + (U3-Eпит)/ R_к = 0 (Є.1)

3. Розрахуємо режим по постійному струму, використовуючи рівняння для третього вузла (вихідна напруга). Для отримання ММС в формі метода вузлових потенціалів загальний вид метода Ньютона -Рафсона:

,

де зліва – вектор-стовбець невідомих напруг вузлів [U^j+1], справа – вектор-стовбець відомих напруг вузлів, які помножені на компоненти матриці провідності, що визначає додаткові струми на поточній ітерації;

J(u^j) – вектор задаючих струмів;

Y(u^j) – матриця провідності схеми на поточній ітерації.

В режимі покою I_сн=Cн*dUcн/dt=0, тому рівняння Є.1 прийме вид

3: _N* Іэ₀*(е^u2/mt-1) + (U3-Eпит)/ R_к = 0 .

Розв’язок цього рівняння для одного невідомого, наприклад, напруги третього вузла, має вид:

тут

= _N* Іэ₀*(е^u2/mt-1) + (U3-Eпит)/ R_к

=1/ Rк.

Приймаємо, що напруга на відкритому транзисторі

U3 ≈ Uкэ_нас ≈ 0.3 В

Uкэ_нас – залишкова напруга на відкритому БТ (напруга насичення).

Підставляючи числові значення, та нехтуючи членами малого порядку, отримаємо:

В якості початкового наближення для третього вузла приймаємо Uкэ_нас .

U₃⁰≈ 0,3 В.

Підставляючи значення, отримаємо на першій ітерації U₁¹≈ 0,31 В.

Визначаємо похибку

Δ = U₁¹ - U₁⁰≈ 0,01 В,

(максимальну абсолютну похибку приймаємо ε _max=0.01). Оскільки значення Δ < ε , ітерації можна припинити.

Таким чином, розраховане значення вихідної напруги в стаціонарному режимі U₃ ≈ 0,31 В. Його приймаємо за початкові умови для розрахунку перехідного процесу.