Тема 5.2. Методы нелинейного программирования при наличии ограничений

Содержание вопросов

Методы аппроксимации. Алгоритм нелинейного программирования. Метод допустимых направлений (метод Зойтендейка). Метод обобщенного приведенного градиента.

Вопросы и задания для самостоятельной работы:

1. Подготовить ответы на контрольные вопросы по теме 5.2.:

1.1. Методы аппроксимации?

1.2. Алгоритм нелинейного программирования?

1.3. Метод допустимых направлений (метод Зойтендейка)?

1.4. Метод обобщенного приведенного градиента?

1.5. Приведенный градиент?

1.6. Направление оптимизационного поиска?

1.7. Метод оптимизационного поиска в заданном направлении с целью нахождения допустимой точки?

2. Тестовые задания для самостоятельного контроля уровня подготовки студентами вопросов темы 5.2.

2.1. Методы аппроксимации:

А. линейная аппроксимация фигурирующих в задаче нелинейных функций достигается путем замены этих функций членами первого порядка в соответствующих разложениях в ряд Тейлора в окрестности рассматриваемой точки ;

Б. в результате повторяющегося процесса линеаризации нелинейных функций путем разложения их в ряд Тейлора в окрестности каждого промежуточного решения образуется последовательность 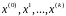, которая при определенных условиях сходится к оптимальному решению …;

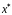В. метод оптимизации, требующий линеаризации только ограничений и не предполагающий линеаризации целевой функции, проиллюстрируйте графически…;

Г. используется идея приведенного градиента: структура данного метода предполагает реализацию линейно-аппроксимирующих процедур; определение новых переменных, ортогональных к некоторым из ограничений; приведение

градиента целевой функции к преобразованному таким способом базису.

2.2. Алгоритм нелинейного программирования:

А. алгоритм Дибелла и Стивенса предназначается для решения задач нелинейного программирования при наличии ограничений только в виде равенств (плюс ограничения, задающие верхний и нижний пределы изменения значений независимых переменных);

Б. алгоритм основан на использовании линейной аппроксимации нелинейных функций в окрестности некоторой допустимой или почти допустимой точки ;

В. идея Дибелла относительно минимизации путем применения градиентного и линейно-аппроксимативного методов получила дальнейшее развитие у Барнса, которому удалось обобщить алгоритм на случай, когда в дополнение к ограничениям в виде равенств имеют место записанные в общем виде ограничения в виде неравенств;

Г. при реализации данного алгоритма в качестве начального могут использоваться как допустимые векторы, так и векторы, выходящие за пределы допустимой области. Если не является допустимым, алгоритм реализует фазу наискорейшего спуска с тем, чтобы получить такой вектор , для которого множество ограничивающих условий «почти» удовлетворяется.

2.3. Метод допустимых направлений (метод Зойтендейка):

А. для каждой допустимой точки в может существовать множество различных допустимых направлений оптимизационного поиска;

Б. поиск начинается в допустимой точке пространства решений и реализуется (при линеаризованных ограничениях) по траектории, обеспечивающей улучшение значений целевой функции и вместе с тем никогда не выходящей за пределы допустимой области;

В. предложенный Розеном метод проекции градиента представляет собой одну из модификаций метода допустимых направлений;

Г. проекция градиента 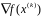на подмножество ограничений, содержащее , задает направление поиска, соответствующее (относительно евклидовой метрики) направлению наискорейшего спуска для целевой функции, тогда как в методе Зойтендейка используется другая метрика, а именно метрика, определяемая соотношением

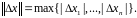
2.4. Метод обобщенного приведенного градиента:

А. алгоритм обобщенного приведенного градиента представляет собой модификацию алгоритма Вольфа, которая может быть использована для решения задач при нелинейном характере и целевой функции и ограничений;

Б. структура данного метода предполагает реализацию (по отношению к нелинейным функциям) линейно-аппроксимирующих процедур;

В. предполагает определение новых переменных, ортогональных к некоторым из ограничений;

Г. предполагает приведение градиента целевой функции к преобразованному таким способом базису.

2.5. Приведенный градиент:

А. ограничения в виде равенств отражают зависимость между переменными задачи лишь в неявной форме, непосредственное сокращение размерности этой задачи … ;

Б. уравнения, задающие ограничения, не могут быть разрешены относительно зависимых переменных с тем, чтобы их можно было путем соответствующих подстановок исключить из структуры целевой функции и, таким образом, выразить целевую функцию только через независимые переменные;

В. метод ограниченных вариаций позволяет сократить размерность задачи и делает возможным использование приведенного градиента в качестве одного из критериев при установлении оптимальности;

Г. для частного случая задачи предположим, что целевая функция зависит всего от двух переменных при единственном ограничении в виде равенства, т.е. рассмотрим задачу: минимизировать 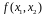при ограничении

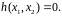
2.6. Направление оптимизационного поиска:

А. алгоритм обобщенного приведенного градиента начинает работу с допустимой точки;

Б. если относительно условий рассматриваемой задачи вектор не является допустимым и, следовательно, возникает необходимость вводить в рассмотрение искусственные переменные, то значения последних постепенно сводят к нулю путем добавления к целевой функции штрафного члена, что в итоге делает вектор допустимым;

В. если приведенный алгоритм ни на одном из этапов вычислительной процедуры не обращается в нуль, производится замена текущего вектора по стандартной формул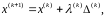е где 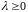, а элементов вектор-столбца 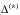задают направление…;

Г. компоненты 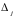, соответствующие независимым (небазисным) переменным, определяются способом, который отличается от способа определения для зависимых (базисных) переменных.

2.7. Метод оптимизационного поиска в заданном направлении с целью нахождения допустимой точки:

А. процедура завершения поиска длины шага, уменьшающего , с использованием как зависимых, так и не зависимых переменных;

Б. каким образом удается подобрать значения зависимых переменных так, чтобы текущее значение получило дополнительную минимизирующую поправку при сохранении вектора внутри или на границе допустимой области;

В. какими должны быть значения в соотношении ;

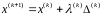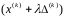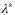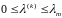Г. значение целевой функции в точке минимизируется при помощи параметра на шаге (т.е. ), значение которого определяется в процессе одномерного дихотомического поиска. Значения лежат в интервале, определяемом , где .
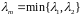