3. Определённый интеграл

3.1. Основные понятия

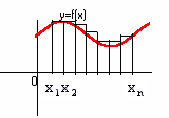
Пусть на отрезке [a; b] определена функция y = f(x). Разобьём отрезок [a;b] на n элементарных отрезков точками . Тогда сумма вида называется интегральной суммой для функции y = f(x) на отрезке [a;b], где ,

, .

Определённым интегралом от функции y = f(x) на отрезке [a;b] называется предел интегральных сумм, т. е. .

Числа a и b называются соответственно нижними и верхними пределами интегрирования, f(x)dx называется подынтегральным выражением, а f(x) – подынтегральной функцией, x – переменной интегрирования, отрезок [a; b] – отрезком интегрирования.

Д

при

остаточным условием интегрируемости функции является её непрерывность на рассматриваемом отрезке

При фиксированных пределах интегрирования интеграл

есть постоянное число. Описанная схема нахождения

определённого интеграла используется для его приближённого вычисления.

Геометрический смысл определённого интеграла: интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Механический смысл определённого интеграла: скорость есть интеграл от ускорения, а пройденный телом путь интеграл от скорости.

3.2. Правила интегрирования

Линейность интеграла а) интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций на отрезке [a;b] б) постоянный множитель можно выносить за знак определённого интеграла	, если k – постоянная
Аддитивность интеграла отрезок интегрирования определённого интеграла можно разбить на части
При перестановке пределов интегрирования знак интеграла изменяется на противоположный
Интеграл с одинаковыми пределами интегрирования равен нулю	, если a = b

3.3. Методы интегрирования

1. Для вычисления определённого интеграла необходимо сначала вычислить соответствующий ему неопределённый интеграл (если это возможно), а затем использовать формулу Ньютона – Лейбница: , т. е. определённый интеграл от непрерывной на отрезке [a; b] функции f(x) равен приращению любой её первообразной F(x) на этом отрезке.

Пример: .

При вычислении определённого интеграла часто используются метод замены переменной и метод интегрирования по частям, которые имеют некоторые отличия от вычисления неопределённого интеграла.

2. Замены переменной в определённом интеграле. Возвращаться к старой переменной не требуется, но необходимо не забывать менять пределы интегрирования, то есть , где .

П ример: 3. Интегрирование по частям определенного интеграла заключается в использовании формулы: .

Пример:

4. Приближенные методы вычисления интегралов. При решении ряда прикладных

Приближенные вычисления
Формула средних прямоугольников
Формула трапеции
Формула парабол (Симпсона)

задач чаще всего приходится сталкиваться с вычислением «неберущихся» определённых интегралов (когда первообразные не выражаются через элементарные функции). Существуют различные формулы для приближённых вычислений определённых интегралов с любой степенью точности.

Пример. Налог на имущество предприятия можно вычислить приближённо по формуле трапеций с разбиением года на 12 месяцев: N= , где f(0) – стоимость имущества на 1 января; f(1) – стоимость имущества на 1 февраля; …; f(11) – стоимость имущества на 1 декабря; f(12) – стоимость имущества на 1 января следующего года.