О.Г. Боровик, С.П. Грушевский, О.В. Засядко, С.П. Шмалько. Интеграл и его приложения в экономике: учебно-методическое пособие / О.Г. Боровик, С.П. Грушевский, О.В. Засядко, С.П. Шмалько; под общ. ред. С.П.Грушевского.
Краснодар: Кубан. гос. ун-т, 2007. 79 с.: ил.
Предлагаемое учебно-методическое пособие содержит комплексы заданий по разделам математического анализа «Неопределённый интеграл», «Определённый интеграл», «Несобственный интеграл». Структурировано по темам, отражающим основные теоретические сведения, даны примеры и блоки учебных заданий, как в традиционных формах, так и с использованием инновационных дидактических технологий. Комплекс представленных задач и упражнений соответствует требованиям государственного образовательного стандарта и обеспечивает профессиональную направленность курса математики для экономистов.
Адресовано студентам экономических специальностей. Может быть полезным преподавателям и всем, кто интересуется проблемами интегралов и их экономическими приложениями.
В
1.Опорный
конспект «Основные формулы интегрального
исчисления» |
Таблица первообразных |
||||
1.
|
2.
|
||||
3.
|
4. |
||||
5.
|
6.
|
||||
7.
|
8.
|
||||
9.
|
10.
|
||||
Правила интегрирования |
|||||
Линейность а) интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций
б) постоянный множитель можно выносить за знак интеграла
|
|||||
Производная неопределённого интеграла равна подынтегральной функции
|
Интеграл с
одинаковыми пределами интегрирования
равен нулю
|
||||
При перестановке пределов интегрирования знак интеграла изменяется на противоположный
|
|||||
Неопределённый интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной
|
Аддитивность интеграла отрезок интегрирования определённого интеграла можно разбить на части
|
||||
|
|
|
|||
|
|||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
,
,
если a=b
ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА |
Механические |
||
Перемещение |
|
||
Работа |
|
||
Масса стержня |
|
||
Электрический заряд |
|
||
Количество теплоты |
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
Геометрические приложения |
|
Площадь плоской фигуры |
|
Объем тела вращения |
|
Длина дуги плоской кривой |
|
Площадь поверхности вращения |
|
,
Структурно-логическая схема «Интеграл и его приложения»
2.Неопределённый интеграл
2.1. Первообразная
Функция F(x) называется первообразной функцией для функции f(x), или интегралом от f(x), если f(x) есть производная функции F(x), т. е. f(x)= F´(x).
Отыскание для данной произвольной функции её первообразной называется интегрированием (а весь комплекс вопросов связанных с этим – интегральным исчислением). Отыскание первообразной является обратной задачей для дифференцирования.
Прямая задача: Обратная задача:
дифференцирование интегрирование
f(x) →f´(x) f(x) = F´(x) → F(x)
П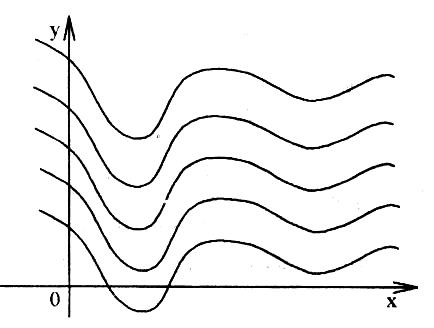
роизводная
от числа равна нулю, т. е. (F(x)+С)´ = F´(x)= f(x).
Поэтому общее выражение F(x)+С
совокупности всех первообразных от
функции f(x)
называется неопределённым интегралом
от этой функции и обозначается
∫f(x)dx
= F(x)+С;
произведение f(x)dx
называется подынтегральным выражением,
а f(x) –
подынтегральной функцией, x
– переменной интегрирования, ∫
– знаком неопределённого интеграла.
Всякая непрерывная функция f(x) имеет бесчисленное множество различных первообразных функций, отличающихся друг от друга постоянным слагаемым.
Геометрически, в системе координат XOY, графики всех первообразных функций от данной функции f(x) представляют семейство кривых, зависящее от одного параметра C, которые получаются одна из другой путём параллельного сдвига вдоль оси OY. График каждой кривой называется интегральной кривой.
2.2. Правила интегрирования
Производная неопределённого интеграла равна подынтегральной функции
|
|
Неопределённый интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной
|
|
Линейность интеграла
а) интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций
б) постоянный множитель можно выносить за знак интеграла
|
|
,
если k – постоянная
2.3. Табличные интегралы
1.
|
2.
|
3.
|
4. |
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
,
2.4. Методы интегрирования
1. Непосредственное интегрирование заключается в сведении данного интеграла к табличному интегралу.
Пример:
.
2. Метод разложения заключается в использовании свойств линейности интеграла.
Пример:
.
3. Интегрирование путём замены переменной
а) метод подведения под знак дифференциала, означает, что функция должна соответствовать дифференциалу: du = d(u + C)
,
С ≠ 0
.
Пример:
;
б) метод письменной замены переменной
(подстановка) заключается в том, что x
меняют на φ(t), где φ(t)
– непрерывно дифференцируемая функция,
и получают
,
причём после интегрирования возвращаются
к старой переменной обратной подстановкой
.
Примеры: 1)
;
2
)
.
4. Интегрирование по частям заключается
в использовании формулы
,
где u и v –
дифференцируемые функции от x.
Применение формулы необходимо в тех
случаях, когда полученный интеграл
будет проще исходного или когда он будет
ему подобен. Этот метод используется
для вычисления интегралов, представленных
в виде двух сомножителей:
1.
;
2 .
;
3.
;
4.
;
5 .
;
6.
;
7.
;
8.
,
где
(x)
– многочлен степени n.
В случаях 1–3 через u обозначают (x), в 4–7 – вторые сомножители, в 8 – любую функцию. А
оставшуюся часть подынтегрального выражения принимают в качестве dv.
Примеры:
1)
2)
Опорный конспект «Методы интегрирования»
№ п/п |
Вид интеграла |
Метод интегрирования |
1 |
1)
;
;
2) ; ; ; ; 3) |
Интегрирование по частям через u обозначают: 1) (x) – многочлен степени n 2) вторые сомножители 3) любую функцию Оставшуюся часть подынтегрального выражения принимают в качестве dv. |
2 |
Если дробь неправильная, то нужно выделить целую часть, разделив числитель на знаменатель, и представить её в виде суммы многочлена и правильной дроби |
Нужно дробь разложить на сумму
и применить метод неопределённых коэффициентов |
3 |
R – рациональная функция |
Подстановка
|
4 |
|
Универсальная подстановка sin
x= x=2arctg t. Если R(–sin x, cos x)= –R(sin x, cos x), то cos x=t. Если R(sin x, –cos x)= –R(sin x, cos x), то sin x=t. Если R(–sin x,–cos x)=R(sin x, cos x), то tg x=t |
5 |
|
Подстановка tg
x=t,
x=arctg
t,
dx= |
6 |
|
Нужно преобразовать произведение тригонометрических функций в сумму или разность sin ax sin bx = [ cos (a–b)x - cos (a+b)x]/2, cos ax sin bx = [ cos (a–b)x + cos (a+b)x]/2, sin ax cos bx = [ sin (a–b)x + sin (a+b)x]/2 |
|
Окончание опорного конспекта «Методы интегрирования» |
|
№ п/п |
Вид интеграла |
Метод интегрирования |
7 |
|
Если m – нечетное, m>0, то cos x = t. Если n – нечетное, n>0, то sin x = t. Если m + n – четное отрицательное, то tg x = t. Если m, n – четные неотрицательные, то понижаем степень по формулам:
sin
x
cos
x= |
9 |
R – рациональная функция |
Приводится к интегралу
от рациональной дроби k
– общий знаменатель
для дробей
|
10 |
|
Подстановка
|
11 |
R – рациональная функция |
Сводится к интегралу от
рациональной дроби подстановкой |
12 |
1) 2) 3) |
Подстановки 1) x=a sin t, 2)x=a tg t,
3)x= |
13 |
m, n, p – рациональные числа (дифференциальный бином) |
1: а) если p – целое положительное число, то нужно раскрыть скобки (a+bxn)p по биному Ньютона и вычислить интегралы от степеней; б) если p – целое отрицательное, то x=tk, k
– общий знаменатель
дробей m, n.
2.
Если k - знаменатель дроби p. 3. Если +p – целое число, то a+bxn=tkxn, k – знаменатель дроби p |
14 |
|
t=ex
, x= |
;
,
где
– правильная
рациональная
дробь,
,
,
, 
.
При этом
,
cos
x=
,
dx=
,
,
m,
n
– целые.
,
,
,
.
, 
,
,
,
– целое
число, то a+bxn=tk,
t,
dx=
интеграл преобразуется в интеграл
от рациональной функции