5. Жордановы матрицы

Опр. Жорданова клетка J_m, – матрица m x m вида

Опр. Жорданова матрица – блочно-диагональные матрицы из жордановых клеток

,

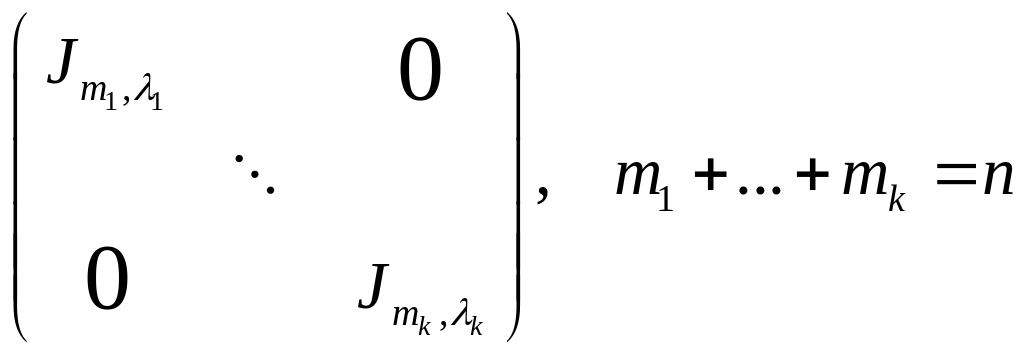Опр. Жорданова матрица A называется жордановой нормальной формой (ЖНФ) матрицы B, если B = C^-1AC, где C – некоторая невырожденная матрица.

Теорема 1. Любая комплексная матрица обладает ЖНФ.

(Уважаемый читатель, огромная просьба: не путать линейные операторы и их матрицы!)

Пусть A – матрица n x n. Рассмотрим пространство V над размерности n (dim V = n), с базисом e₁, …, e_n. Пусть : VV – линейный оператор с матрицей A в этом базисе. Для A существует корневое разложение , где – собственные числа . Зафиксируем одно из подпространств: и рассмотрим действие на U оператора  =  - . Тогда действие  на U нильпотентно (по доказанному ранее) и также по доказанной теореме  разложение циклических подпространств. По предыдущему следствию в U есть базис, в котором  имеет блочно диагональную матрицу B = 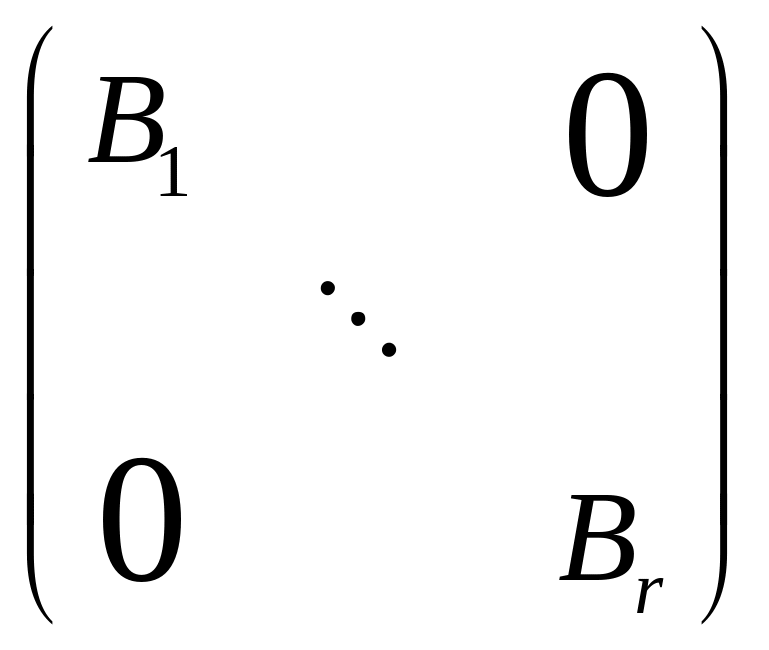, а каждая B_j – жорданова клетка с  = 0. Поскольку  =  + _i, то (U_j)  U_j и в том же базисе U оператор  имеет матрицу A = B + _iE = 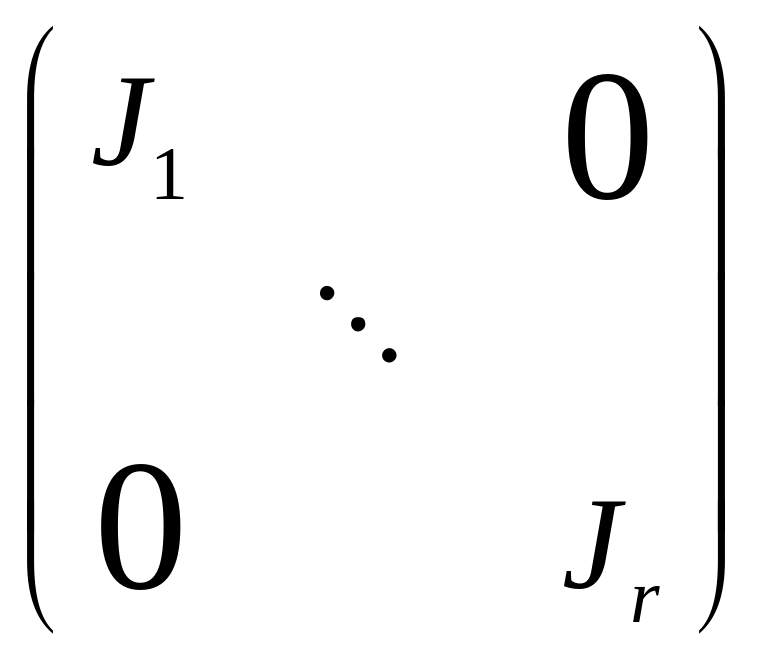, где все J₁, …,J_r – жордановы клетки вида . Рассмотрев отдельно все мы поcтроим базис пространства V, в котором матрица A является жордановой матрицей T. Если C – матрица перехода , то T = C^-1AC. 

Следствие. Для любого линейного оператора на конечномерном комплексном пространстве можно выбрать базис, в котором матрица оператора является жордановой матрицей.

6. Единственность жнф

Теорема 2. ЖНФ матрицы A единственна с точностью до перестановки клеток.

Пусть A – жорданова матрица n x n. 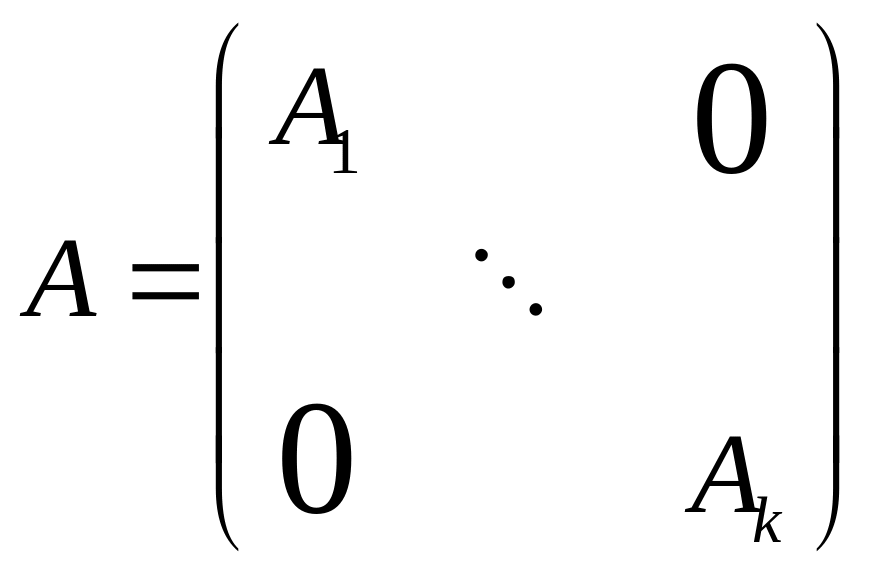, где - жордановы клетки.

Обозначим: - число клеток J_m, среди . Сначала выведем формулу для . Пусть : VV – линейный оператор на n-мерном пространстве с матрицей A.

Обозначим: Тогда Здесь - единичные матрицы соответствующих размеров.

1) Если и , то 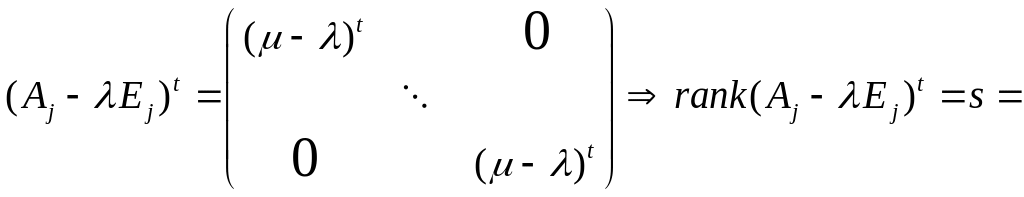размер (A_j).

2) Если , то - матрица нильпотентного оператора  =  -  на циклическом (для ) подпространстве U. Вычислим Пусть v, v, …, ^s-1v – циклический базис для  в U. Тогда ^t(U) = < ^tv, …, ^s-1v> (или 0, если ). Отсюда , если t < s и u = 0 если .

3) Найдем разность для A. Пусть - размеры всех клеток среди с собственным числом . Тогда для клеток с числом имеем разность можно считать только по клеткам с . Поэтому Т.е. - число клеток J_m, среди , у которых . Отсюда ) - ( - число клеток J_k+1,  формула , где

Пусть A и D матрицы двух жордановых нормальных форм одного оператора с матрицей В. Тогда: ( - некоторая матрица), . Поэтому

(т.к. F является невырожденной). Преобразование мы использовали следующее: . Таким образом, . Это и есть единственность. 

28.02.05

БИЛИНЕЙНЫЕ ФОРМЫ

1. Определение.

F – поле, V – векторное пространство над эти полем.

Опр. Функция называется билинейной формой, если она линейна по каждому аргументу. То есть :

1)

2)

2. Матрица билинейной формы.

Пусть - базис V. Обозначим .

Опр. называют матрицей билинейной формы f в базисе .

Координатная запись. , . Тогда :

, где

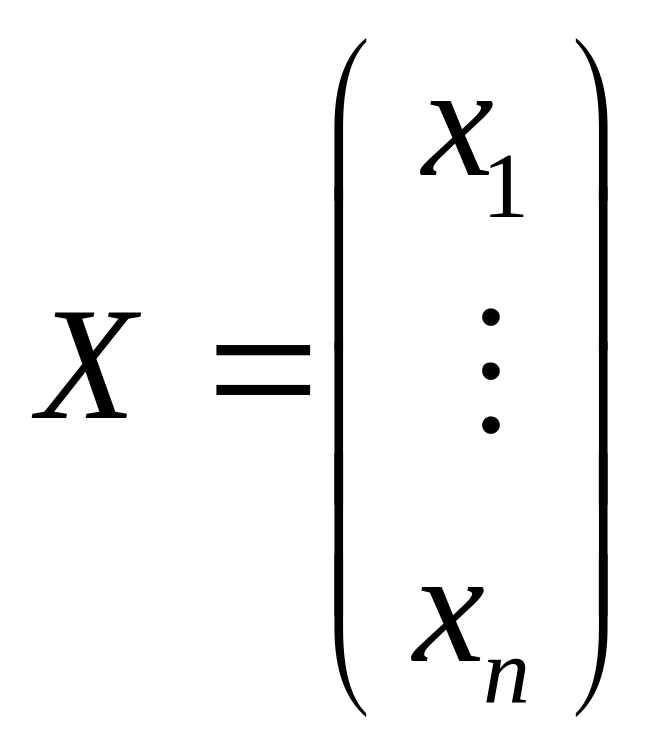, , , а .