3. Нильпотентные операторы

Определение. ℬ - нильпотентный оператор, если ∃m≥1: ℬ^m = 0.

Утверждение. Если ℬ нильпотентен на и , то ℬ = 0.

По теореме Гамильтона-Кэли , . Если , то всё доказано. Пусть теперь . Подставим в многочлен . Тогда существует выражение (наименьшая степень выражается через старшие) для некоторого . Так как нильпотентен, существует : . Если , то и подавно , если , то (домножая равенство двумя строками выше на , пока слева не будет ) получим, что . Провернув это доказательство для этой обнуляющей степени несколько раз получим .

Другое [более нормальное, народ, пользуйтесь им] доказательство того, что :

1) Если , то минимальный многочлен ( ) (так как он делит аннулирующий многочлен ).

2) По теореме Гамильтона-Кэли и определению минимального многочлена делится на .

Лемма 2. Пусть , – собственное значение . Тогда – инвариантное для подпространство и действует на нильпотентно.

1) Инвариантность

Пусть . Докажем, что . . . Итак .

2) Нильпотентность действия

Положим . Выберем базис . Тогда . Если , то .

3. Разложение в сумму корневых подпространств

Теорема. Пусть , , где при . Тогда выполняется:

1)

2) Все инвариантны относительно действия .

3) Действие на нильпотентно.

4)

5) Единственным собственным значением на является .

Доказательство.

1) Положим . Тогда . Пусть – произвольный вектор из . , , где .

Таким образом . Следовательно, . Эта сумма прямая по лемме 1.

2), 3) – лемма 2.

5) Пусть и . Тогда – это одно из чисел . Если , то .

4) Выберем базисы во всех подпространствах и объединим их. Мы получим базис во всём пространстве . В этом базисе имеет матрицу 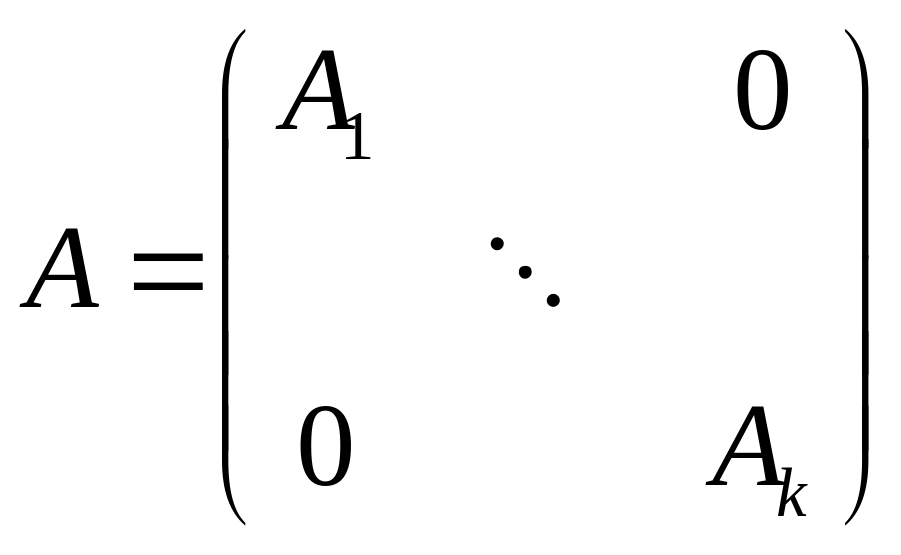, где – квадратная матрица размера , . Обозначим через ограничение на , т.е , . Тогда имеет матрицу и только одно собственное значение .

. .

4. Нормальный базис для нильпотентного оператора

Пусть оператор нильпотентный, – подпространство в .

– циклическое подпространство для оператора , если , , .

Свойства циклического подпространства:

1) – инвариантное подпространство для (т.е. ) – по определению.

2) – базис

То, что любой вектор выражается через этот базис – очевидно.

Докажем линейную независимость.

26.02.05

Теорема. Пусть  – нильпотентный оператор на V. Тогда V можно разложить в сумму циклических подпространств для .

Доказательство.

Индукция по dim V. Если dim V = 1, то V = <v>,  v = 0.

Пусть dim V > 1. Обозначим U = (V). Если U = 0, то V – прямая сумма одномерных циклических подпространств. Пусть U  0. Ясно, что (U)  U.

Шаг 1: Т.к. ker   0, то dim U < dim V (по инд.) – сумма циклических подпространств, где U₁ = <u₁, u₁, …>, … ,U_k = <u_k, u_k, …>. Т.к. U = (V), то u₁ = v₁,…, u_k = v_k. Докажем, что векторы , u₁,…, u_k, u₁,…,u_k… (все ненулевые векторы вида ^m(v_j)) линейно независимы. Пусть w = ₁v₁ + … + _kv_k + ₁u₁ + … + _ku_k + … = 0. Применим : ₁u₁ + … + _ku_k + ₁u₁ + … + _ku_k + … = 0. Т.к. это линейная комбинация базисных векторов пространства U, то все коэффициенты ₁, … _k, ₁, …, _k, … равны нулю.

Шаг 2: Обозначим за W_i = <v_i, u_i, u_i,…>. Это циклическое подпространство для , и, по доказанному в Шаге 1, их сумма – прямая, . Теперь докажем, что (W) = U. Включение (W)  U очевидно. Пусть Тогда x = ₀u_i + ₁u_i + … + _m^mu_i. Пусть y = ₀v_i + ₁u_i + … + _m^m-1u_i. Тогда y = x. Если то y_i = x_i  (y₁ +… + y_k) = x  (W) = U.

Шаг 3: Если W = V, то теорема доказана. Пусть W  V. Тогда , линейно независимые, и Заменим на следующим образом:

– если w_j = 0,

– если w_j = x_j  0, то y_i = x_i (см. Шаг 2). В этом случае положим

Шаг 4: Векторы обладают следующими свойствами:



2)

3) – линейно независимы

Докажем, например, 2). Если , то все _i = 0. ( 3) – аналогично). Из 1), 2), 3) следует, что – разложение V в сумму циклических подгрупп для . 

Следствие. Пусть : VV – нильпотентный оператор на V. Тогда  базис V, в котором матрица  имеет вид 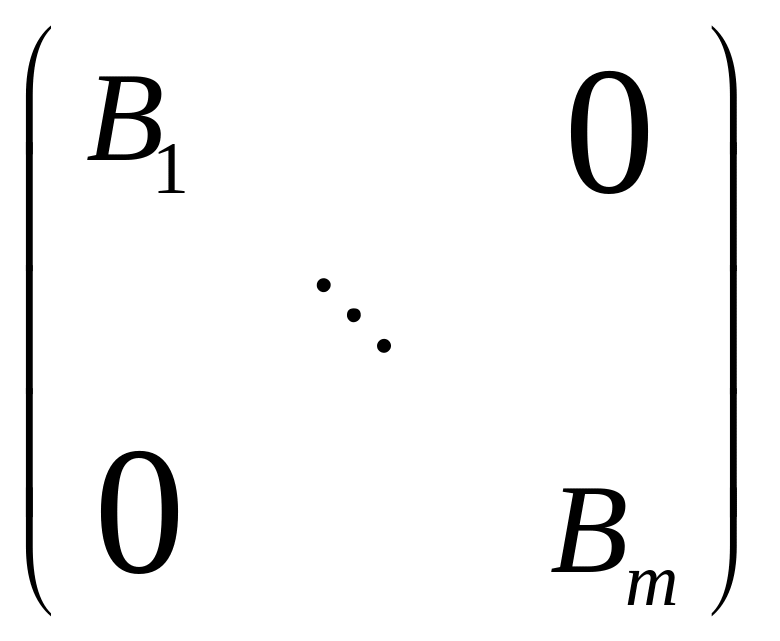 = , где B_i – квадратные матрицы вида

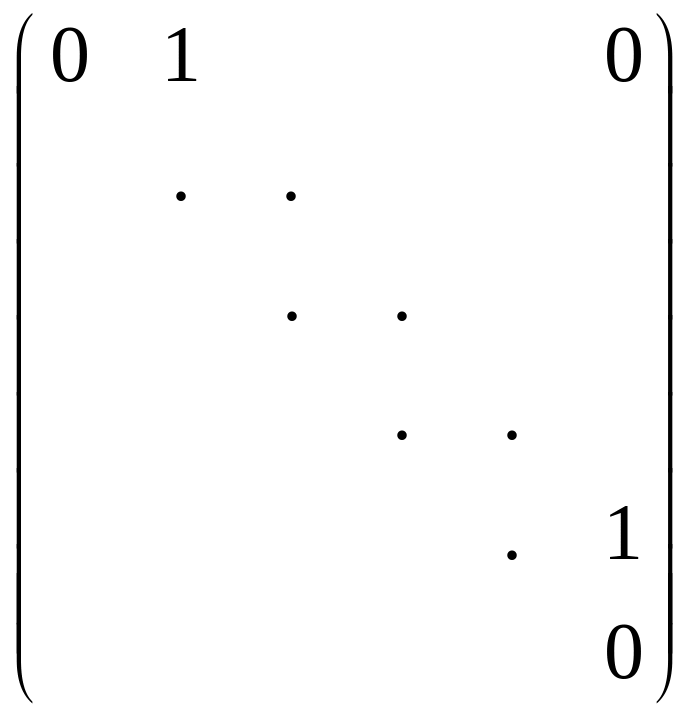
Разложим V в прямую сумму циклических подпространств для оператора . В каждом циклическом подпространстве U = <u, u, …, ^tu> , ^t+1u = 0 выберем базис e₁ = ^tu, e₂ = ^t-1u, …, e_t+1 = u. Объединяя эти базисы, получаем наше утверждение. 