5. Минимальный многочлен оператора

Пусть A , , где - единичный оператор.

Опр. - аннулирующий многочлен для оператора А, если

Опр. называется минимальным многочленом А, если

1. - аннулирующий многочлен.

2. Любой другой аннулирующий многочлен делится на без остатка.

Лемма. существует и определен однозначно (с точностью до скалярного множителя)

(а) Существование аннулирующих многочленов.

Пусть А – матрица А. Тогда матрицы линейно зависимы, если N > n² , где , т.е. , где - аннулирующий многочлен.

(б) Существование минимального аннулирующего многочлена.

Пусть и - два аннулирующих многочлена для А и - НОД.

Тогда тоже аннулирующий многочлен аннулирующий многочлен степени k

(в) Единственность минимального аннулирующего многочлена.

Пусть - аннулирующий многочлен степени k, - аннулирующий многочлен.

Тогда их НОД тоже аннулирующий многочлен степени k, делит , но это значит, что = НОД(f,g), а значит делится на минимальный аннулирующий многочлен, кроме того, мы так же доказали и его единственность

6. Теорема Гамильтона-Кэли

Пусть

Теорема. (оператор А аннулируется своим характеристическим многочленом)

Обозначим ,

Тогда и существует собственный вектор

Построим базис , где . Тогда матрица А в этом базисе имеет вид:

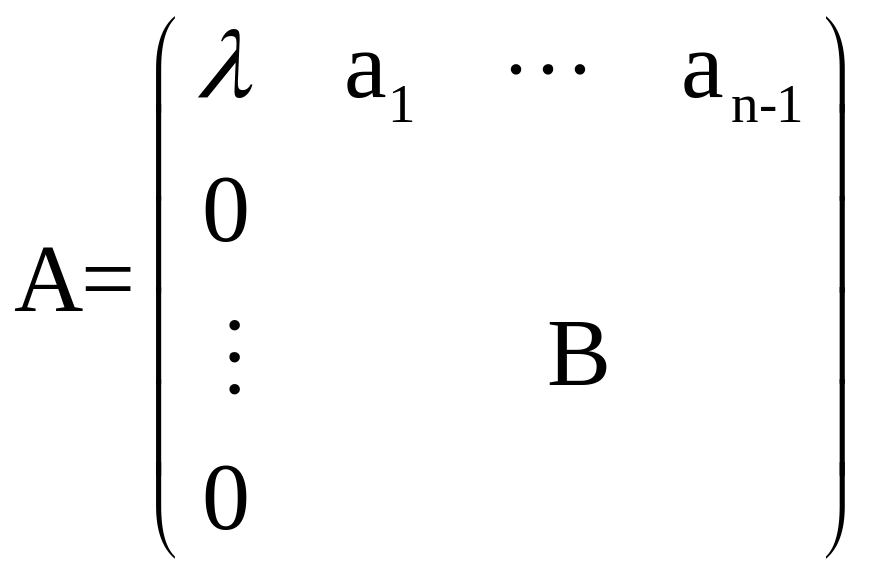, где B – матрица (n-1)x(n-1)

Поэтому

Положим и обозначим через B линейный оператор с матрицей B в базисе . Так как то можем применить индукцию по (с базой n = 1). Итак, пусть . Тогда, так как , то . Вычислим . Ясно, что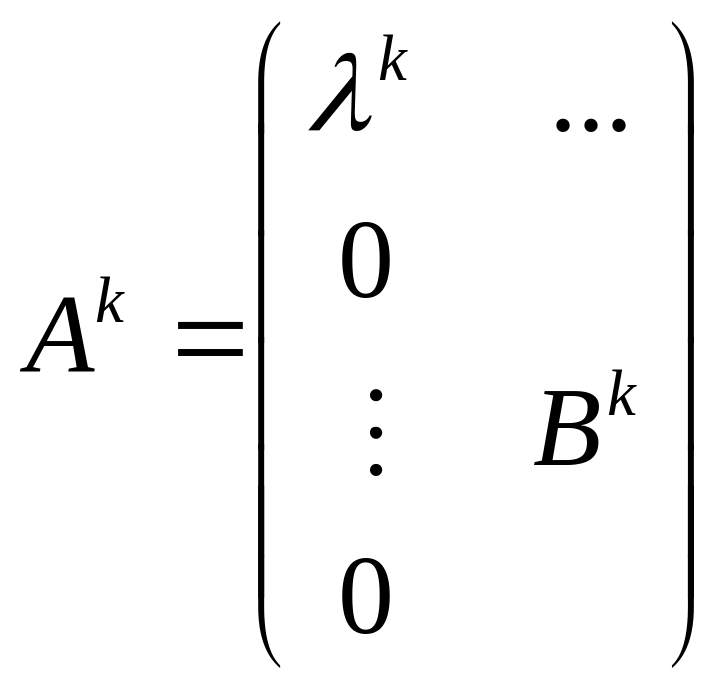 , а следовательно , .

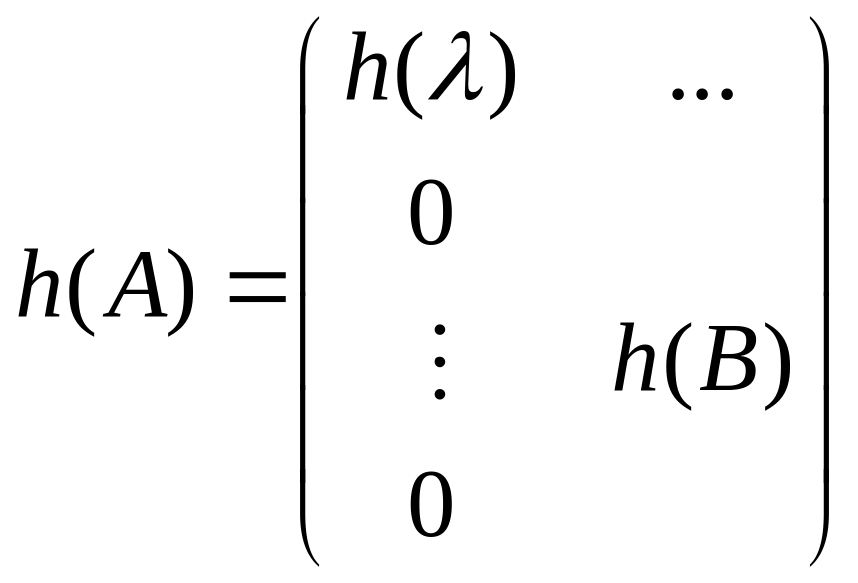
С другой стороны, 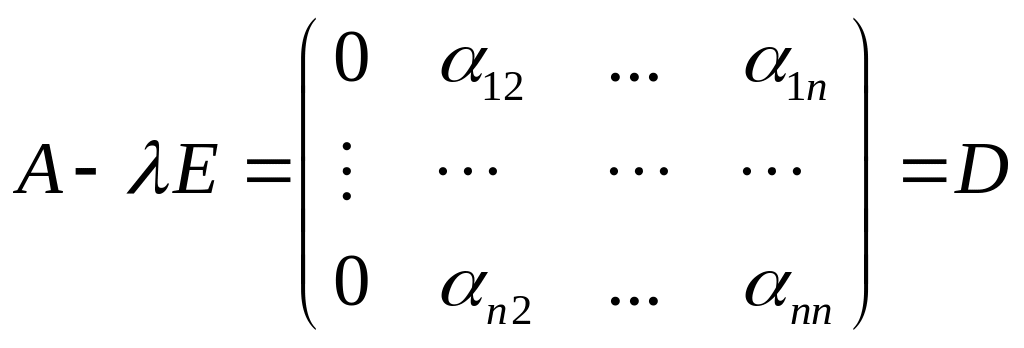. Очевидно, что

Подполя в

Примеры:

Следствие 1. Пусть - пространство над , . Тогда .

Пусть А --- матрица А в некотором базисе .Рассмотрим n-мерное пространство над и оператор B на этом пространстве с той же матрицей А. Тогда . По теореме Гамильтона-Кэли: , т.е. , что и требовалось доказать.

Следствие 2.

1. Характеристический многочлен делится на минимальный

2. Если - корень , то - корень

(1) следует из теоремы Гамильтона-Кэли и определения

(2) Пусть - все комплексные корни . Пусть - корень . Тогда . Так как , то

Заметим, что . Поэтому

Но . Значит, , т.е. - один из

Жорданова нормальная форма

В этом разделе будем считать, что , – векторное пространство, над , . Эту теорию можно развивать над любым полем, но наиболее важные результаты получаются, когда поле замкнуто.

1. Корневое подпространство

Пусть , – собственное значение оператора на .

Рассмотрим (при это определение собственного подпространства). Тогда выполняется:

1) (собственное подпространство принадлежит ).

2) В частности, из 1) следует, что .

3) – подпространство в . (доказательство очевидно: если , то ).

– корневое подпространство, отвечающее корню .

Лемма 1. Пусть , , … – различные собственные значения . Тогда .

Пусть . Если , то , где . .

Обозначим и .

Тогда: , .

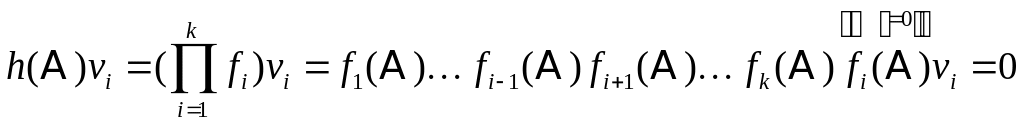Таким образом, если вектор принадлежит и , то он равен .