1. Определение.
Базис
{
}
пространства
,
такой, что
называется
дуальным (или сопряжённым) к
базису {
}
пространства
.
Обозначим за
пространство,
сопряжённое
.
Тогда, как мы уже знаем,
.
Мы уже говорили, что два пространства
изоморфны, если они имеют равные
размерности, но в данном случае, кроме
того, можно установить особое соответствие:
канонический изоморфизм.
2. Определение.
Отображение
называется каноническим изоморфизмом
и задаётся следующим образом: если
- это вектор из
,
то
.
Это и есть определение
Проверим,
что отображение
--- изоморфизм между
и
.
Для начала --- что линейная функция.
1) Проверим, что
,
то есть линейная функция из
в
:
,
то есть
--- действительно линейное отображение
из
в
,
что означает, что это отображение задано
корректно.
2) Проверим линейность отображения
(сначала то, что сумма переходит в сумму).
,
то есть мы проверили, что
.
,
то есть
.
Наконец, нужно проверить, биективно ли
отображения
.
Инъективность. Пусть
,
где
--- базис
(то есть мы взяли вектор
из
и разложили его по базису
).
Если
--- дуальный базис
,
то
.
Так как хотя бы один
,
то и
.
То есть
.
Следовательно,
--- инъективное отображение (разные
векторы имеют разные образы), потому
что для линейного множества достаточно
проводить проверку для «0», что мы уже
только что проделали.
Сюръективность. Пусть
и обозначим
.
Возьмём
.
Тогда
,
то есть
.
Значит,
сюръективно, а из этого следует, что
- биекция. Таким образом,
--- изоморфизм.
Теорема.
Векторы
линейно независимы тогда и только тогда,
когда
,
такие что:
.
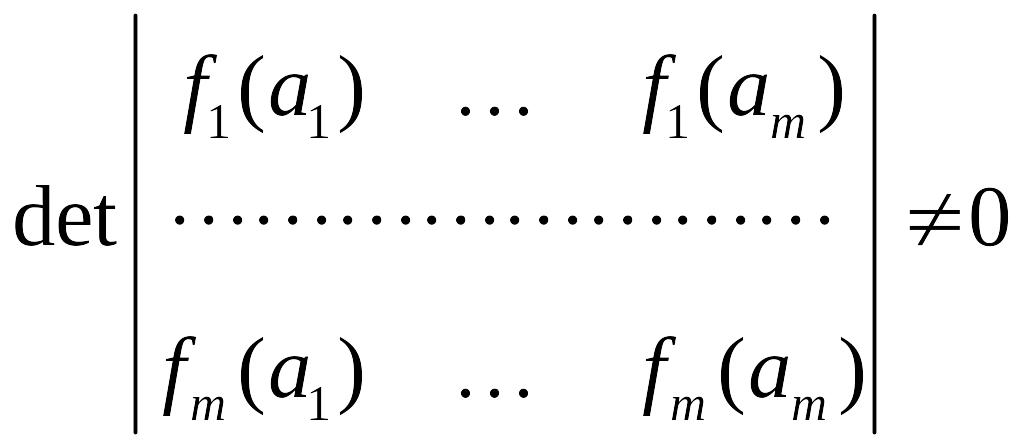1) Пусть
линейно зависимы, то есть существуют
коэффициенты
(хотя бы один отличен от 0), такие что
.
Пусть
--- столбцы матрицы (*). Тогда для любых
линейная комбинация столбцов
.
2) Теперь пусть
--- линейно независимы. Дополним до базиса
:
и возьмём дуальный базис
.
Тогда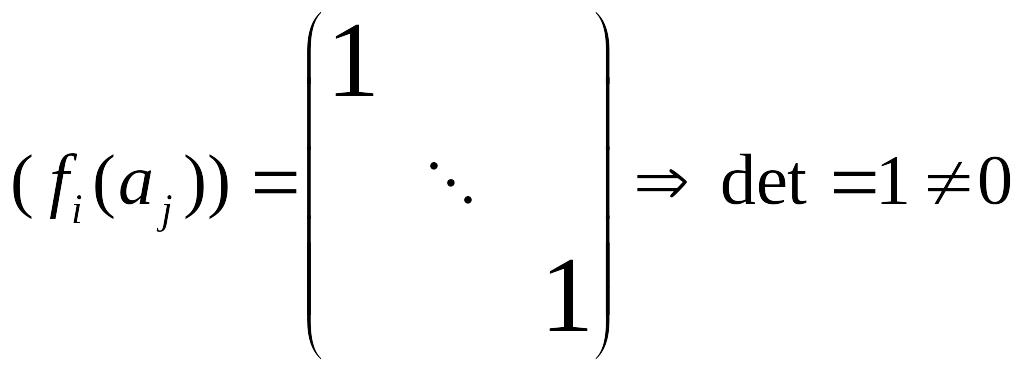
,
что и требовалось доказать.
Пусть
и
--- множество векторов
из
,
таких, что
обращаются в
.
То есть,
является решением системы линейных
уравнений
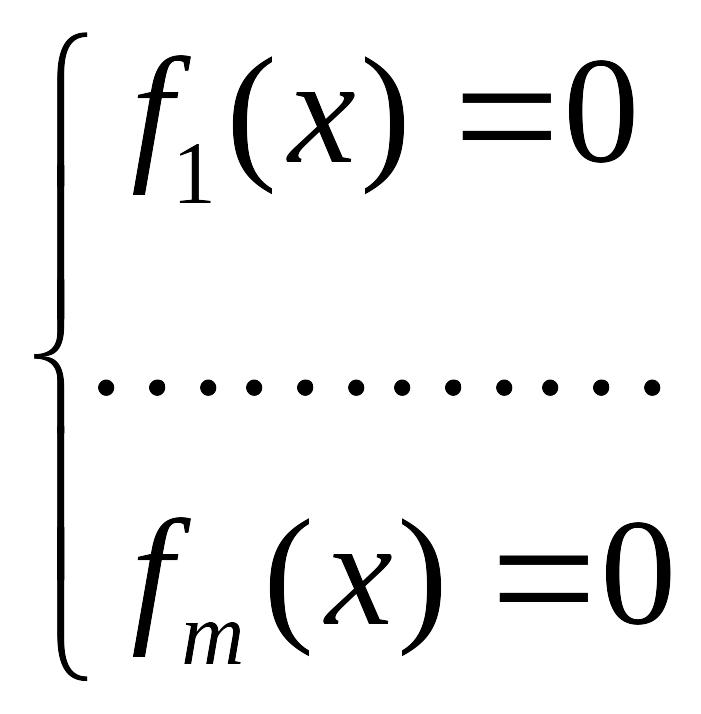
Теорема. 1) Пусть
.
Тогда
,
где
.
2) Любое подпространство
является пространством решений
некоторой системы
.
1) Пусть сначала
--- линейно независимы. Тогда дополним
до базиса
в
и возьмём дуальный базис
в
,
тогда эти базисы связаны со следующим
соотношением:
.
Пусть
.
Тогда
,
то есть
в этом случае
,
причём
.
Если же
линейно зависимы, то существует
максимальная линейно независимая
подсистема, например,
,
такая что
.
Но тогда если
,
то
.
То есть
(см. выше) отсюда мы уже доказали, что
,
следовательно, 1) доказано.
2) Пусть
--- любое подпространство. Выберем базис
в
так, что
.
Если
--- дуальный базис
,
то
Следствие 1. Множество решений
однородной системы линейных уравнений
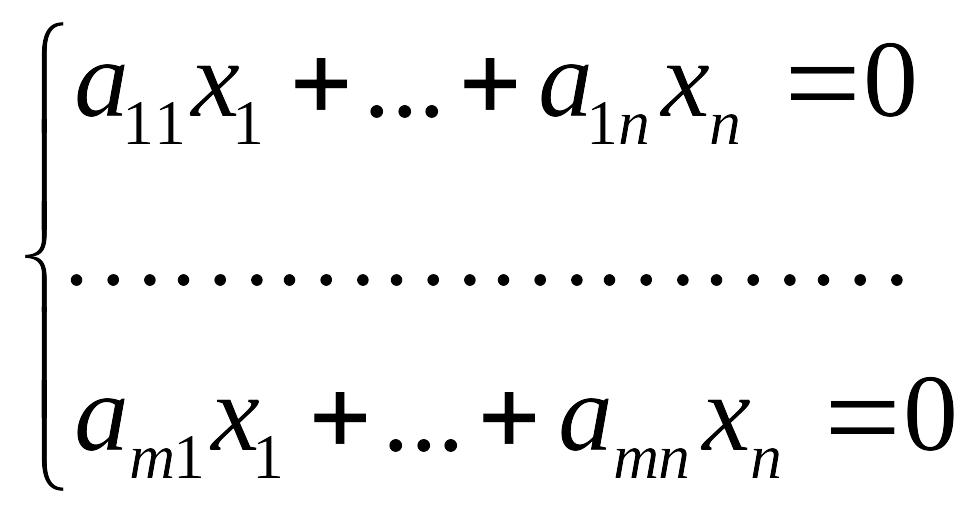является подпространством в
арифметическом пространстве 
.
Следствие 2. Любое подпространствo в является пространством решений некоторой однородной системы линейных уравнений.
Пусть 
– подпространство. По предыдущей теореме
существуют
,
такие, что: 
.
Если --- базис , --- базис (дуальный), то
.
Если
,
то
