Тензорная алгебра векторного пространства

Опр. A - алгебра над полем F, если

1) A – ассоциативное кольцо с операциями

2) A – векторное пространство над F.

3)

Рассмотрим бесконечную прямую сумму . , где K - поле, V – векторное поле над ним.

Опр. Пространство с умножением , где называется тензорной алгеброй пространства V. Она ассоциативна.

Рассмотрим в подпространство . Позже мы покажем, что эта сумма на самом деле конечна (т.е. все слагаемые начиная с некоторого равны нулю). Это подпространство, однако оно не замкнуто относительно тензорного умножения, т.е. не является подалгеброй , поэтому на нем мы введем новое умножение.

Внешняя алгебра векторного пространства (алгебра грассмана)

1. Внешнее умножение.

Опр. Если , то - внешнее умножение. Если , то и считаем, что . Также верна дистрибутивность .

Опр. Пространство с операцией внешнего умножения называется внешней алгеброй (алгеброй Грассмана) пространства V.

2. Ассоциативность внешнего произведения.

Лемма. Пусть . Тогда .

Так как - линейное отображение и , то . Сопоставим подстановке подстановку по следующему правилу:

Это отображение в . Знак и совпадает. Итак,

. Поэтому . Аналогично, .

Теорема. Внешняя алгебра ассоциативна.

Нужно доказать равенство . Так как внешнее умножение линейно, то левая и правая часть формулы (1) линейны по . Поэтому доказать (1) для частного случая .

.

3. Базис внешней алгебры.

Пусть . Тогда . Тогда .

Следствие.

Для проверено. Далее по индукции:

30.04.05

4. Связь с определителями

Теорема. Пусть - векторное пространство над полем и . Тогда векторы линейно независимы в том и только в том случае, если .

Пусть сначала линейно зависимы. Обозначим через их линейную оболочку. Тогда . Из следствия (см. предыдущую лекцию) получаем что , а с другой стороны . Следовательно .

Пусть теперь линейно независимы. Тогда в существует базис , такой, что . В этом случае - один из базисных элементов (см. теорему из предыдущей лекции) алгебры . Поэтому .

Замечание. . Если - произвольный элемент , то не всегда .

Пусть теперь , - базис , и . Их внешнее произведение можно явно выразить через произведения . Пусть - координаты вектора в базисе , т.е. . Введём обозначение:

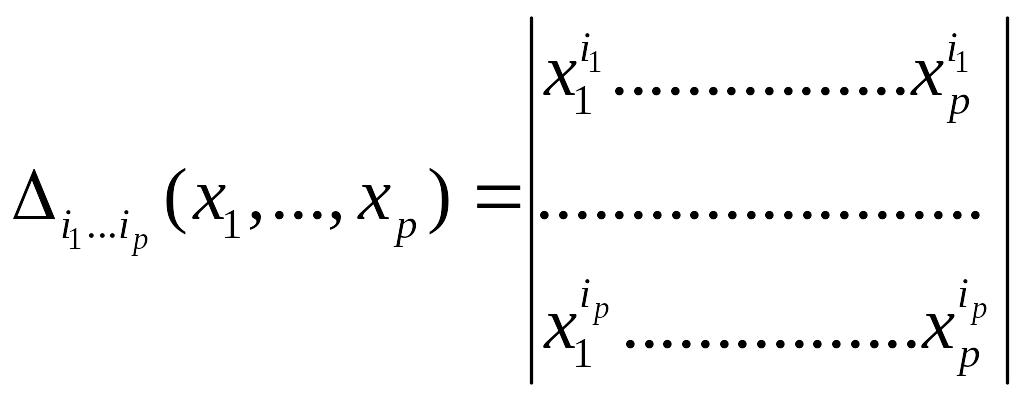
В матрице, столбцы которой – координаты векторов , вычеркнуты все строки, кроме .

Теорема. Пусть - базис , и , - любые векторов в . Тогда

.

Рассмотрим в этой сумме ту часть слагаемых, у которых множество одно и то же. Слагаемые этой суммы отличаются только порядком следования этих индексов, т.е. эта часть суммы равна . При этом произведение равно , где знак подстановки , а сами можно считать упорядоченными: . Поэтому .

Вспомним формулу для определителя . Отсюда следует, что . Это означает, что множитель перед равен .

7 мая 2005

78