
- •Зайцев м. В. Лекции по линейной алгебре.
- •1. Определения.
- •2. Линейная зависимость.
- •4. Матрицы перехода от базиса к базису.
- •5. Координаты в различных базисах.
- •6. Изоморфизм векторных пространств.
- •Подпространство
- •1. Определение.
- •2. Линейная оболочка.
- •3. Сумма и пересечение двух подпространств.
- •4. Прямая сумма подпространств.
- •Линейные и сопряженные пространства
- •1. Определение.
- •2. Определение.
- •Линейные отображения и операторы
- •1. Линейные отображения.
- •2. Задание линейных отображений матрицами.
- •Характеристический многочлен оператора
- •1. Определения
- •2. Геометрическая и алгебраическая кратность.
- •3. Спектр оператора
- •4. Диагонализируемые операторы
- •5. Минимальный многочлен оператора
- •6. Теорема Гамильтона-Кэли
- •Жорданова нормальная форма
- •1. Корневое подпространство
- •Нильпотентные операторы
- •3. Разложение в сумму корневых подпространств
- •4. Нормальный базис для нильпотентного оператора
- •5. Жордановы матрицы
- •6. Единственность жнф
- •1. Определение.
- •2. Матрица билинейной формы.
- •3. Изменение матрицы билинейной формы при замене базиса.
- •4. Симметрические и кососимметрические билинейные формы.
- •5. Канонический базис для симметрической билинейной формы.
- •6. Квадратичные формы
- •7. Алгоритм Лагранжа (приведения к каноническому виду).
- •8. Вещественные квадратичные формы
- •9. Теорема Якоби.
- •10. Положительно определенные квадратичные формы.
- •11. Канонический вид кососимметричной бф
- •Евклидовы пространства
- •3. Угол между векторами
- •4. Ортогональные векторы
- •5. Изоморфизм евклидовых пространств
- •6. Процесс ортогонализации Грамма-Шмидта
- •6. Ортогональные дополнения
- •8. Сопряжённые операторы
- •9. Самосопряжённые операторы
- •10. Приведение квадратичной формы к главным осям.
- •Ортогональные операторы
- •1. Основные понятия
- •2. Канонический базис для ортогонального оператора.
- •3. Полярное разложение.
- •Унитарные пространства
- •1. Эрмитовы (полуторалинейные) формы.
- •2. (Эрмитово) скалярное произведение.
- •3. Ортогональность.
- •4. Унитарные и эрмитовы матрицы.
- •6. Сопряжённый оператор.
- •6. Эрмитовы операторы.
- •7. Унитарные операторы.
- •Аффинные точечные пространства
- •2. Изоморфизм
- •3. Координаты в аффинном пространстве.
- •4. Подпространства.
- •Евклидовы точечные пространства
- •1. Евклидова метрика.
- •2. Расстояние от точки до плоскости.
- •3. Расстояние между плоскостями.
- •Квадрики в аффинном пространстве
- •1. Квадратичные функции в аффинном пространстве
- •2. Координатная запись
- •3. Центральная точка
- •4. Нахождение центра
- •5. Приведение квадратичной функции к каноническому виду.
- •Тензоры
- •1. Основные понятия.
- •2. Интерпретация тензоров малых рангов.
- •3. Произведение тензоров.
- •4. Координаты тензоров.
- •5. Изменение координат тензора при замене базиса
- •6. Свёртки тензоров.
- •Кососимметричные тензоры
- •Тензорная алгебра векторного пространства
- •Внешняя алгебра векторного пространства (алгебра грассмана)
- •1. Внешнее умножение.
- •2. Ассоциативность внешнего произведения.
- •3. Базис внешней алгебры.
- •4. Связь с определителями
6. Свёртки тензоров.
Пусть
-
тензор типа
.
Зафиксируем числа
![]() и
и
![]() ,
и определим свёртку по r-ому ковариантному
индексу и s-ому контрвариантному индексу
следующим образом. Т.к.
,
и определим свёртку по r-ому ковариантному
индексу и s-ому контрвариантному индексу
следующим образом. Т.к.
![]() ,
где
,
где
![]() ,
а
,
а
![]() ,
то можно определить сумму
,
то можно определить сумму
![]() ,
где
- базис
,
а
- дуальный базис
.
,
где
- базис
,
а
- дуальный базис
.
Определение.
![]() называется свёрткой тензора
по r-ому ковариантному индексу и s-ому
контрвариантному индексу.
называется свёрткой тензора
по r-ому ковариантному индексу и s-ому
контрвариантному индексу.
Ясно, что
- полилинейная функция от оставшихся
аргументов, т.е.
![]() .
Докажем, что
не зависит от выбора базиса пространства
.
.
Докажем, что
не зависит от выбора базиса пространства
.
Доказательство: пусть
- другой базис пространства
,
а
- матрица перехода от базиса
к базису
.
Тогда
![]() .
Напомним, что для дуальных базисов
имеем:
.
Напомним, что для дуальных базисов
имеем:
![]() ,
где
(смотри доказательство предыдущей
теоремы). Зафиксируем для удобства все
остальные переменные у
кроме
,
где
(смотри доказательство предыдущей
теоремы). Зафиксируем для удобства все
остальные переменные у
кроме
![]() и
и
![]() ,
обозначим
,
обозначим
![]() .
Тогда
.
Тогда
![]() .
Получаем:
.
Получаем:
![]() .
.
Заметим, что
![]() - произведение i-ой строки матрицы
на j-ый столбей матрицы
.
Т.к.
- произведение i-ой строки матрицы
на j-ый столбей матрицы
.
Т.к.
![]() эта сумма равна
эта сумма равна
![]() ,
.
,
.
23.04.2005
Связь
координат тензора T и его
свертки
![]() .
.
Теорема. Свертка по s-тому ковариантному и r-тому контравариантному индексам тензора T типа (p,q) является тензором типа (p-1,q-1) с координатами
![]()
То,
что свертка – тензор типа
![]() - проверено. Пусть
- проверено. Пусть
![]() ,
где
,
где
![]() .
Как и раньше, обозначим через
.
Как и раньше, обозначим через
![]() .
Обозначим
.
Обозначим
![]() .
Тогда
.
Тогда
![]()
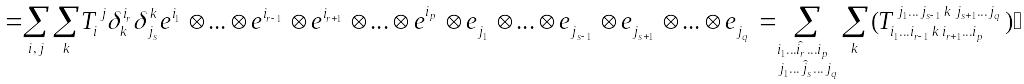
![]() .
.
Знак
«домик» означает пропуск соотв. индекса
(т.е.
![]() ).
Соотношение (1) и есть утверждение
теоремы.
).
Соотношение (1) и есть утверждение
теоремы.
Пример.
Тензор типа (1,1)
![]() - это матрица
.
Его свертка равна
- это матрица
.
Его свертка равна
![]() - след матрицы A.
- след матрицы A.
Действие симметрической группы на тензорах.
Пусть
T – тензор типа
![]() ,
т.е.
,
т.е.
![]() ,
и
,
и
![]() - группа подстановок множества
- группа подстановок множества
![]() .
Для любой
.
Для любой
![]() определим отображение
определим отображение
![]() .
Ясно, что
.
Ясно, что
![]() - тензор типа
.
Аналогично можно определить действие
- тензор типа
.
Аналогично можно определить действие
![]() на
на
![]() .
.
Опр.
Тензор T типа
называется симметричным, если
![]() .
.
Ясно,
что
![]() - линейный оператор на
- линейный оператор на
![]() .
.
Опр.
Симметризацией тензоров из
называется отображение
![]() .
.
Пример.
![]() Возьмем подстановку
Возьмем подстановку
![]() .
Тогда
.
Тогда
![]()
![]() .
.
![]() .
.
Обозначим
через
![]() подпространство всех симметричных
тензоров из
.
подпространство всех симметричных
тензоров из
.
Теорема. Действие симметризации на обладает следующими свойствами:
1)
![]() и 2)
и 2)
![]() .
.
(а)
Если T – симметричный тензор, то
![]() .
.
(б) Покажем, что симметризация любого
тензора симметрична.
![]() .
Из формулы
.
Из формулы
![]() получаем
получаем
![]() (т.к.
(т.к.
![]() ).
Пункт (б) означает, что
).
Пункт (б) означает, что
![]() .
Теперь из (а) следует, что
и из (б) и (а) следует 1).
.
Теперь из (а) следует, что
и из (б) и (а) следует 1).
Кососимметричные тензоры
Опр.
Тензор
![]() называют кососимметричным, если
называют кососимметричным, если
![]() ,
где
,
где
![]() - знак подстановки. Эквивалентно,
- знак подстановки. Эквивалентно,
![]() .
Кососимметричные тензоры образуют
подпространство в
.
Кососимметричные тензоры образуют
подпространство в
![]() ,
которое принято обозначать
,
которое принято обозначать
![]() .
.
Опр. Элементы (т.е. p раз контравариантные кососимметричные тензоры) называют внешними p-формами или внешними формами степени p на V.
Аналогично
вводятся множество кососимметричных
контравариантных тензоров на
![]() (название – q-вектора).
(название – q-вектора).
25.04.05
Опр.
Отображение
![]() на
пространстве
(или
)
называют альтернированием.
на
пространстве
(или
)
называют альтернированием.
Теорема. Отображение A является линейным оператором на со следующими свойствами:
1)
![]() 2)
2)
![]() 3)
3)
![]()
1)
Поскольку
![]() ,
то
,
то
![]() ,
учитывая, что
,
учитывая, что
![]() и
и
![]() .
При фиксированном
.
При фиксированном
![]() и при
и при
![]() ,
пробегающем все подстановки из
произведение
,
пробегающем все подстановки из
произведение
![]() также пробегает
.
Поэтому
также пробегает
.
Поэтому
![]() и не зависит от
.
Следовательно
и не зависит от
.
Следовательно
![]() .
.
2)
Пусть
.
Тогда
![]() ,
а значит (по определению)
-
кососимметричный тензор, откуда и
следует
,
а значит (по определению)
-
кососимметричный тензор, откуда и
следует
![]() .
Обратное включение следует из того, что
для всякого кососимметричного тензора
.
Обратное включение следует из того, что
для всякого кососимметричного тензора
![]() .
.
3)
Равенство
![]() доказывается так же, как и равенство
доказывается так же, как и равенство
![]() (см. пред. пункт).
(см. пред. пункт).
Замечание. Отличие теоремы для
только в том, что
![]() .
.
