3. Произведение тензоров.

Пусть сначала , - два произвольных полилинейных отображения, где - различные векторные пространства (не обязательно совпадают) над .

Определение: Тензорное произведение и , где .

Ясно, что - полилинейная функция по каждому аргументу. Если - три полилинейных функции, то , т.е. тензорное произведение ассоциативно. Но, вообще говоря, оно не является коммутативным, т.е. для произвольных функций (об этом даже не всегда корректно говорить).

Пусть теперь - тензор типа , - тензор типа . Тогда - тензор типа , определённый формулой: (2)

Определение: Тензор, заданный формулой (2) называется тензорным произведением тензоров , .

4. Координаты тензоров.

Пусть - базис . Рассмотрим в сопряжённом пространстве дуальный базис . Т.е. .

Обозначим через пространство тензоров типа на . Тогда любое произведение

(3)

является тензором типа , т.е. полилинейной функцией: . Эти тензоры линейно независимы по следующей причине: (4)

Теорема. Тензоры вида (3) образуют базис векторного пространства .

То, что - пространство – очевидно, если определить сложение обычным образом:

. Умножение на скаляр – тоже обычное. Линейная независимость (3) уже показана. Осталось проверить, что любой тензор линейно выражается через систему (3). Пусть . Обозначим (5). Тогда из формулы (4) следует, что если взять тензор 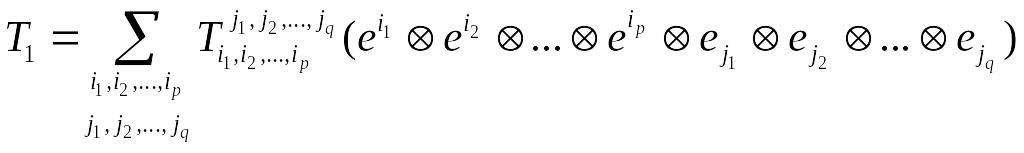, то , т.е. значения и на всех возможных наборах базисных векторов совпадают. Т.к. и - полилинейные функции, то , и (3) – базис пространства .

Определение: Принято говорить, что из формулы (5) – координаты тензора в базисе .

Следствие: .

18 апреля 2005

5. Изменение координат тензора при замене базиса

Пусть и - два базиса в пространстве . Обозначим через матрицу перехода от базиса к базису . Элементы матрицы индексируем так: , где - элемент i-ой строки и j-ого столбца. Тогда имеем:

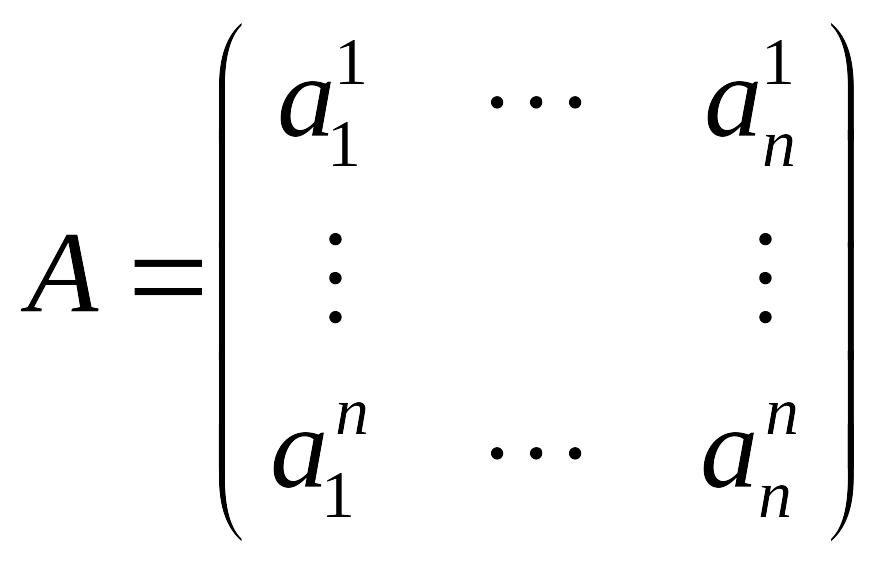и .

Это стандартное обозначение: чтобы суммирование велось по индексу, встречающемуся сверху и снизу. В некоторых книгах знак суммы опускают и пишут: . Но мы так делать не будем: все суммы будем прописывать полностью.

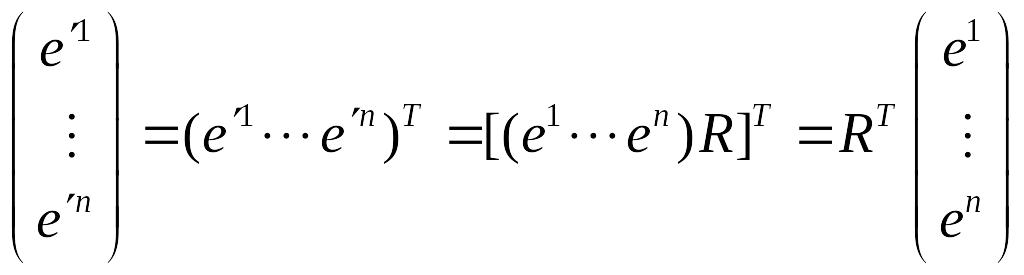Пусть теперь - дуальный базис к базису , а - дуальный к базису в пространстве . Обозначим через матрицу перехода от базиса к базису в пространстве . Тогда . Чтобы следовать правилу “разных уровней” ( т.е. чтобы индекс суммирования появился сверху и снизу), обозначим через - транспонированная матрица . Тогда . Эту формулу мы запишем следующим образом. Поскольку , то , т.е. 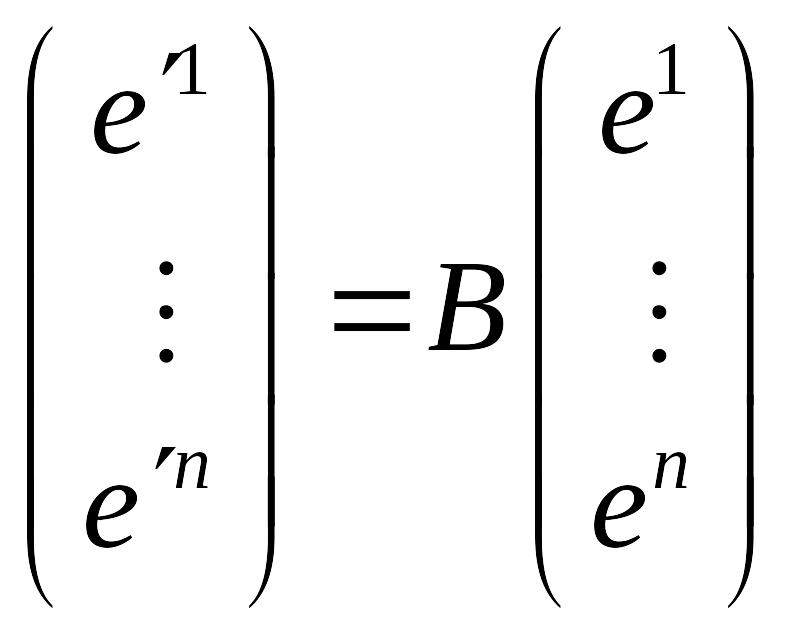. Введём вспомогательную матрицу . Тогда 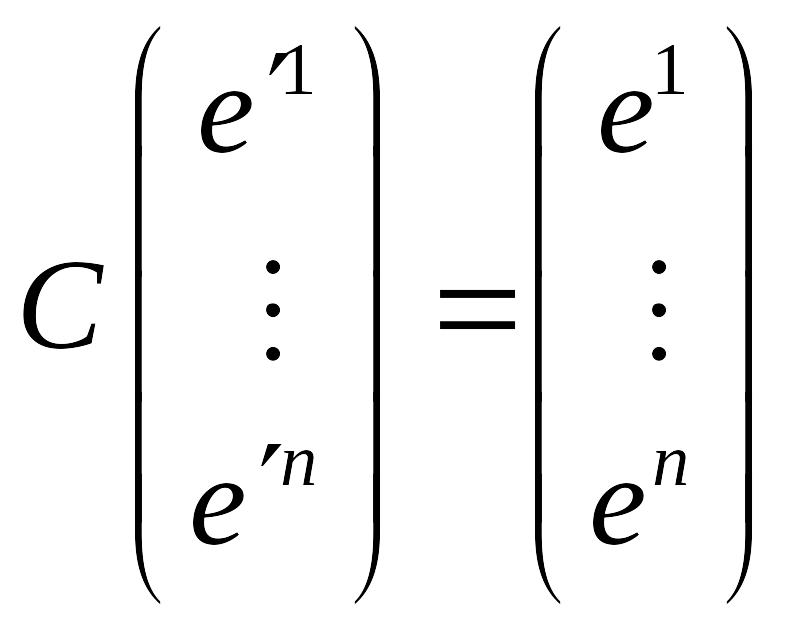, т.е. . Т .к. базисы дуальны . Т.е. и . Отсюда .

Пусть теперь и - его координаты в , а - координаты в базисе . Тогда

, .

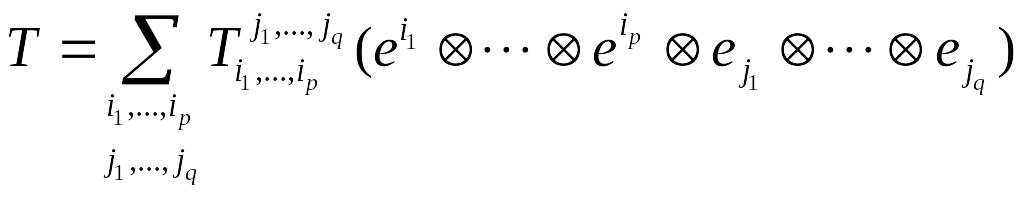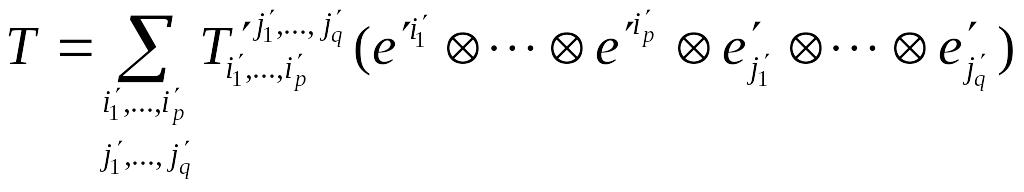(6)

Выразим (аналогично выражаем ) и подставим в формулу (6). Получим

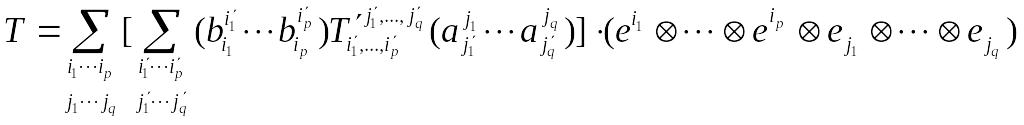. Здесь мы использовали, что и аналогичные выражения для . Т.к. элементы образуют базис пространства , то нами доказана следующая

Теорема. При переходе от базиса к базису в координаты тензора типа изменяются по правилу: 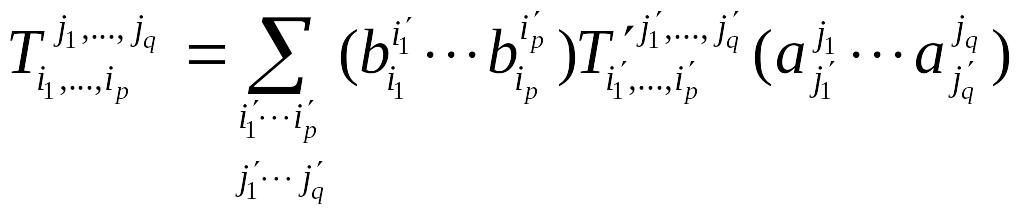, где - матрица перехода от базиса к базису пространства , а .