
- •Зайцев м. В. Лекции по линейной алгебре.
- •1. Определения.
- •2. Линейная зависимость.
- •4. Матрицы перехода от базиса к базису.
- •5. Координаты в различных базисах.
- •6. Изоморфизм векторных пространств.
- •Подпространство
- •1. Определение.
- •2. Линейная оболочка.
- •3. Сумма и пересечение двух подпространств.
- •4. Прямая сумма подпространств.
- •Линейные и сопряженные пространства
- •1. Определение.
- •2. Определение.
- •Линейные отображения и операторы
- •1. Линейные отображения.
- •2. Задание линейных отображений матрицами.
- •Характеристический многочлен оператора
- •1. Определения
- •2. Геометрическая и алгебраическая кратность.
- •3. Спектр оператора
- •4. Диагонализируемые операторы
- •5. Минимальный многочлен оператора
- •6. Теорема Гамильтона-Кэли
- •Жорданова нормальная форма
- •1. Корневое подпространство
- •Нильпотентные операторы
- •3. Разложение в сумму корневых подпространств
- •4. Нормальный базис для нильпотентного оператора
- •5. Жордановы матрицы
- •6. Единственность жнф
- •1. Определение.
- •2. Матрица билинейной формы.
- •3. Изменение матрицы билинейной формы при замене базиса.
- •4. Симметрические и кососимметрические билинейные формы.
- •5. Канонический базис для симметрической билинейной формы.
- •6. Квадратичные формы
- •7. Алгоритм Лагранжа (приведения к каноническому виду).
- •8. Вещественные квадратичные формы
- •9. Теорема Якоби.
- •10. Положительно определенные квадратичные формы.
- •11. Канонический вид кососимметричной бф
- •Евклидовы пространства
- •3. Угол между векторами
- •4. Ортогональные векторы
- •5. Изоморфизм евклидовых пространств
- •6. Процесс ортогонализации Грамма-Шмидта
- •6. Ортогональные дополнения
- •8. Сопряжённые операторы
- •9. Самосопряжённые операторы
- •10. Приведение квадратичной формы к главным осям.
- •Ортогональные операторы
- •1. Основные понятия
- •2. Канонический базис для ортогонального оператора.
- •3. Полярное разложение.
- •Унитарные пространства
- •1. Эрмитовы (полуторалинейные) формы.
- •2. (Эрмитово) скалярное произведение.
- •3. Ортогональность.
- •4. Унитарные и эрмитовы матрицы.
- •6. Сопряжённый оператор.
- •6. Эрмитовы операторы.
- •7. Унитарные операторы.
- •Аффинные точечные пространства
- •2. Изоморфизм
- •3. Координаты в аффинном пространстве.
- •4. Подпространства.
- •Евклидовы точечные пространства
- •1. Евклидова метрика.
- •2. Расстояние от точки до плоскости.
- •3. Расстояние между плоскостями.
- •Квадрики в аффинном пространстве
- •1. Квадратичные функции в аффинном пространстве
- •2. Координатная запись
- •3. Центральная точка
- •4. Нахождение центра
- •5. Приведение квадратичной функции к каноническому виду.
- •Тензоры
- •1. Основные понятия.
- •2. Интерпретация тензоров малых рангов.
- •3. Произведение тензоров.
- •4. Координаты тензоров.
- •5. Изменение координат тензора при замене базиса
- •6. Свёртки тензоров.
- •Кососимметричные тензоры
- •Тензорная алгебра векторного пространства
- •Внешняя алгебра векторного пространства (алгебра грассмана)
- •1. Внешнее умножение.
- •2. Ассоциативность внешнего произведения.
- •3. Базис внешней алгебры.
- •4. Связь с определителями
Евклидовы точечные пространства
1. Евклидова метрика.
Опр.
Аффинное пространство
![]() называется евклидовым точечным
пространством, если
-
евклидово векторное пространство.
называется евклидовым точечным
пространством, если
-
евклидово векторное пространство.
Опр.
Расстояние между точками:
![]()
Свойства
метрики
![]() :
:
i)
![]()
ii)![]()
iii)![]() - неравенство треугольника
- неравенство треугольника
Опр.
Система координат
![]() называется
прямоугольной, если
называется
прямоугольной, если
![]() - ортонормированный базис
.
- ортонормированный базис
.
Опр.
Отображение
![]() называют изоморфизмом евклидовых
пространств
называют изоморфизмом евклидовых
пространств
![]() и
и
![]() ,
если
-
изоморфизм аффинных пространств и
,
если
-
изоморфизм аффинных пространств и
![]()
Теорема. Любые два евклидовых пространства одинаковой размерности изоморфны.
Пусть
и
![]() прямоугольные системы координат в
прямоугольные системы координат в
![]() и
и
![]() .
.
Зададим
![]() .
.
![]() ,
,
![]() .
Тогда
изоморфизм
аффинных пространств, а
.
Тогда
изоморфизм
аффинных пространств, а
![]() сохраняет
длины векторов, т.е.
- изоморфизм евклидовых точечных
пространств.
сохраняет
длины векторов, т.е.
- изоморфизм евклидовых точечных
пространств.
2. Расстояние от точки до плоскости.
Пусть
- евклидово пространство,
![]() ,
,
![]() и
и
![]() -
точки из
.
Прямую, проходящую через
и
будем обозначать как
-
точки из
.
Прямую, проходящую через
и
будем обозначать как
![]() .
Пусть
.
Пусть
![]() - плоскость размерности
в
,
- плоскость размерности
в
,
![]() и
и
![]() .
.
Опр.
Прямая
перпендикулярна плоскости
,
если
![]() ,
т.е.
,
т.е.
![]() .
.
Предложение.
Если
,
,
![]() и
и
![]() ,
то
,
то
![]()
![]() .
Из
следует
.
Из
следует
![]() .
.
![]() .
.
Пусть
теперь
![]() ,
-подпространство
в
,
,
,
-подпространство
в
,
,
![]() -
базис
,
-
базис
,
![]() - базис
.
- базис
.
Теорема.
Из точки
можно опустить перпендикуляр
![]() к
,
.
Его длина
к
,
.
Его длина
![]() есть кратчайшее расстояние от
до
.
Точка
находится из условия
есть кратчайшее расстояние от
до
.
Точка
находится из условия
![]() ,
,
(*)
где
![]() ,
а
,
а
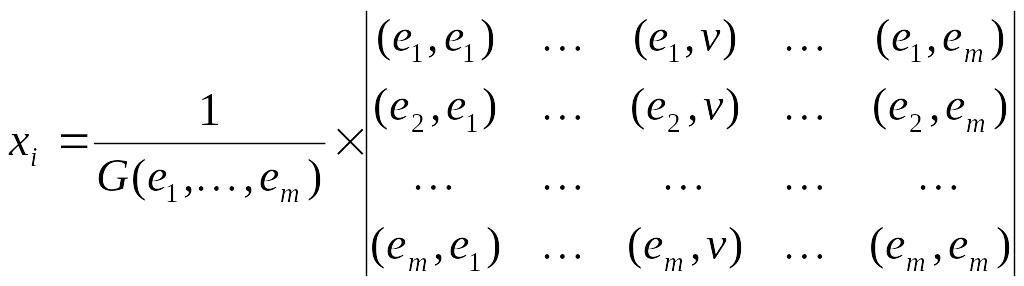
где
![]() ,
а
,
а
![]() - определитель Грама.
- определитель Грама.
![]() Тогда
Тогда
![]() .
Положим
.
Положим
![]() ,
,
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то![]() ,т.е.
,т.е.
![]() .
.
Вычислим
координаты
в
базисе
![]() .
.
Тогда
![]() Отсюда
Отсюда
![]()
Получаем
систему уравнений
![]()
![]() Ее определитель, это
- определитель Грама. Не равен нулю, т.к.
вектора линейно независимы. По правилу
Крамера система имеет единственное
решение задаваемое (*).
Ее определитель, это
- определитель Грама. Не равен нулю, т.к.
вектора линейно независимы. По правилу
Крамера система имеет единственное
решение задаваемое (*).
3. Расстояние между плоскостями.
Пусть
и![]() - две плоскости в евклидовом пространстве
- две плоскости в евклидовом пространстве
![]()
Опр.
Отрезок
![]() - общий перпендикуляр к
и
,
если
- общий перпендикуляр к
и
,
если
![]() и
и
![]() .
.
Лемма 1. Любые две плоскости имеют общий перпендикуляр.
Пусть
![]() ,
,
![]() .
Будем искать точки
.
Будем искать точки
![]() ,
,
такие
что
и
.
Т.к.
![]() ,
то
,
то
![]() .
Разложим V в сумму
.
Разложим V в сумму
![]() .
Тогда
.
Тогда
![]() .
Тогда
.
Тогда
![]() и
и
![]() определены
однозначно, причем
определены
однозначно, причем
![]() .
Отсюда
.
Отсюда
![]() .
Если взять
.
Если взять
![]() ,
то
,
то
![]() .
Т.е.
.
Т.е.
![]() поэтому
- общий перпендикуляр к
и
.
поэтому
- общий перпендикуляр к
и
.
Лемма
2. Если отрезок
- общий перпендикуляр к
и
,
то
![]() .
.
Пусть
![]() ,
,![]() ,
,![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() .
.
![]() .
Т.к.
- общий перпендикуляр к
и
,
то
.
Т.к.
- общий перпендикуляр к
и
,
то
![]() . Следовательно
. Следовательно
![]()
Теорема.
Для любых двух плоскостей
и
в
найдутся такие точки
,
что выполнено
и отр.
- общий перпендикуляр к
и
,
он определен однозначно
![]() .
(
u
.
(
u
![]() - направляющие плоскости
и
).
- направляющие плоскости
и
).
Существование
доказано в Лемме 1 и Лемме 2. Пусть
![]() и
и
![]() -
два перпендикуляра.
-
два перпендикуляра.
Тогда
![]() ,
так что
,
.
Как и в Лемме2
,
так что
,
.
Как и в Лемме2
![]() (*). Поскольку
и
два
перпендикуляра, то
(*). Поскольку
и
два
перпендикуляра, то
![]() .
Следовательно
.
Следовательно
![]() .
Таким образом при
.
Таким образом при
![]() общий перпендикуляр только один. Если
же
общий перпендикуляр только один. Если
же
![]() ,
то
,
то
![]() ,
то и
,
то и
![]() -
общий перпендикуляр.
-
общий перпендикуляр.
2.04.05
Определитель Грама и объем параллелепипеда.
Пусть E – евклидово аффинное пространство,
V – ассоциированное с ним векторное евклидово пространство
![]() ,
,
![]() ,
,
![]() -
ортонормированный базис
-
ортонормированный базис
![]()
Опр.
Параллелепипед в E, заданный
точками
![]()
Объем
зададим так:
![]()
Теорема.
![]()

Заметим,
что
![]() ,
,
![]() ;
;
![]()
Итак,
![]() .
.
Аффинная группа
Пусть
(A,V) – n-мерное аффинное пространство,
и
![]() -биективное
аффинно-линейное отображение, то есть
-биективное
аффинно-линейное отображение, то есть
![]() .
Обозначим
.
Обозначим
![]() .
Так как f-биективное, то
.
Так как f-биективное, то
![]() .
.
Покажем,
что
![]() - тоже аффинное-линейное. Для этого
покажем, что
- тоже аффинное-линейное. Для этого
покажем, что
![]()
Так
как
![]() ,
то
,
то
![]() .
Но
.
Но
![]() ,
,
![]() .
То есть
- аффинно-линейное.
.
То есть
- аффинно-линейное.
Есть
тождественное отображение
![]() .
Оно аффинно-линейное, его дифференциал
.
Оно аффинно-линейное, его дифференциал
![]()
Так как умножение ассоциативно, то можно взять все биективные аффинно-линейные отображения A в себя (операция композиции), получим группу.
Осталось проверить только, что композиция задана корректно.
Теорема.
Совокупность ![]() всех аффинных биективных преобразований
(т.е. аффинно-линейное отображение
)
образует группу.
всех аффинных биективных преобразований
(т.е. аффинно-линейное отображение
)
образует группу.
Не доказано только, что если f и g – аффинно-линейные, то и fg - тоже аффинно-линейное.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
то есть
,
то есть
![]() -аффинно-линейное
с дифференциалом
-аффинно-линейное
с дифференциалом
![]() .
.
Самые простые преобразования – параллельные переносы и сдвиг.
Опр.
Отображение
![]() ,
,
![]() называют
сдвигом на
называют
сдвигом на
![]() в
A, где
в
A, где
![]() .
.
Если
![]() ,
то есть
,
то есть
![]() -аффинно-линейное
отображение
-аффинно-линейное
отображение
![]() .
Оно биективно, значит
- аффинное преобразование.
.
Оно биективно, значит
- аффинное преобразование.
Ясно,
что
![]() .
.
![]() - абелева подгруппа в
- абелева подгруппа в
![]() .
G- группа, f- ее подгруппа.
.
G- группа, f- ее подгруппа.
Опр.
![]() (H - нормальная подгруппа в G), если
она выдержанно сопряжена любым групповым
элементам, т.е.
(H - нормальная подгруппа в G), если
она выдержанно сопряжена любым групповым
элементам, т.е.![]() .
.
![]() -группа
всех невырожденных матриц над полем K.
-группа
всех невырожденных матриц над полем K.
Теорема (о структуре аффинной группы).
1)
Подгруппа сдвигов T –
нормальная в
,
и равна ядру гомоморфизма ![]() , где
, где
![]() .
.
2)
Аффинное преобразование, оставляющее
неподвижной некоторую точку
![]() ,
образующую подгруппу, изоморфную
.
,
образующую подгруппу, изоморфную
.
Доказательство.
1) Мы
уже доказали, что![]()
![]()
Это
и означает, что
![]() гомоморфизм
групп
гомоморфизм
групп ![]() ,
,
![]()
Гомоморфизм сюръективен.
Пусть
теперь![]() .
Тогда
.
Тогда
![]() .
.
Докажем, что этим свойством обладает только сдвиг.
Заметим,
сначала, что если
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() .
.
Поэтому
![]() .
.
Вектор
![]() не зависит от
не зависит от
![]() ,
так как если
,
так как если
![]() ,
то
,
то
![]() .
.
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
то есть
,
то есть
![]() .
В ядре, кроме сдвигов, ничего нет.
.
В ядре, кроме сдвигов, ничего нет.
2)
Очевидно, что
![]() -подгруппа
в An.
Так как
-подгруппа
в An.
Так как
![]() не содержит сдвигов, то ограничение D
на H инъективный гомоморфизм
не содержит сдвигов, то ограничение D
на H инъективный гомоморфизм
![]() .
Покажем теперь его сюръективность.
Построим нужное аффинное преобразование.
Пусть
.
Покажем теперь его сюръективность.
Построим нужное аффинное преобразование.
Пусть
![]() ,
где F произвольный невырожденный оператор
на V.
,
где F произвольный невырожденный оператор
на V.
Тогда
если
![]() ,
то
,
то
![]() ,
то есть f-аффинное преобразование,
причем
,
то есть f-аффинное преобразование,
причем
![]() и
и
![]() .
.
Следовательно,
![]() -изоморфизм
групп.
-изоморфизм
групп.
Теорема.
Любое аффинное преобразование
можно
представить в виде композиции
![]() ,
где
,
где
![]() .
.
Возьмем
![]() ,
положим
,
положим
![]() .
Тогда g-аффинно-линейное
преобразование.
.
Тогда g-аффинно-линейное
преобразование.![]() .
Очевидно,
.
.
Очевидно,
.
Координатная запись аффинных преобразований
Пусть
система
координат в аффинном пространстве
и
![]() –аффинное
преобразование с линейной частью
–аффинное
преобразование с линейной частью
![]() .
.
Пусть
F – матрица
![]() в
базисе
,
а
– координаты точки
в
базисе
,
а
– координаты точки
![]() в той же системе координат, то есть
в той же системе координат, то есть
![]() .
p - точка с координатами
.
.
p - точка с координатами
.
Тогда
![]() .
Если
.
Если
![]() - координаты вектора
- координаты вектора![]() ,
то
,
то
![]() .
.
То
есть
![]() .
Отсюда
.
Отсюда
![]() и
если
и
если
![]() –
координаты
–
координаты
![]() ,то
,то
![]() или
или
![]() ,
где
,
где
 .
.
4 апреля 2005
n=3 Примеры движений
Собственное
В екторное
движение – поворот вокруг некоторой
прямой и сдвиг на вектор, параллельный
оси вращения, т.е.
екторное
движение – поворот вокруг некоторой
прямой и сдвиг на вектор, параллельный
оси вращения, т.е.
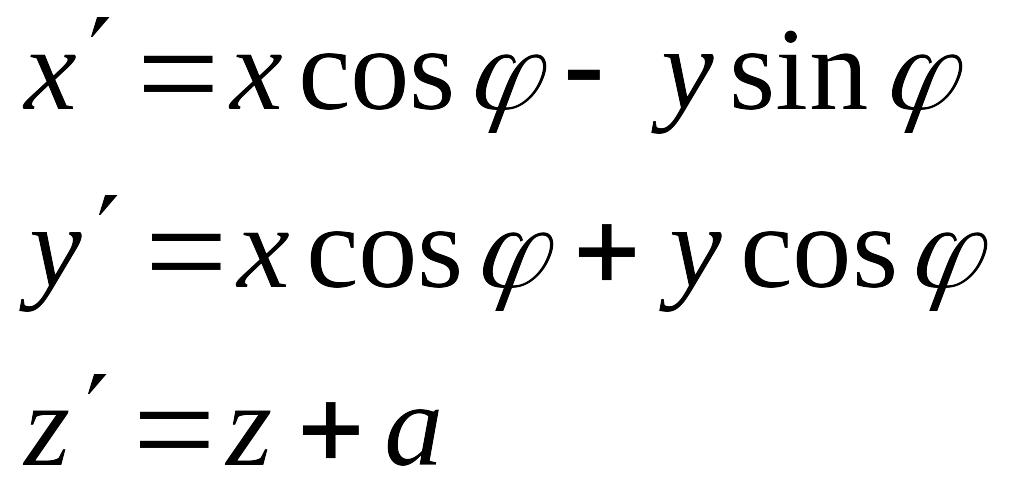

Ч астные
случаи – сдвиг или вращение
астные
случаи – сдвиг или вращение
Н есобственное
есобственное
1

 )
вращение с отражением
)
вращение с отражением
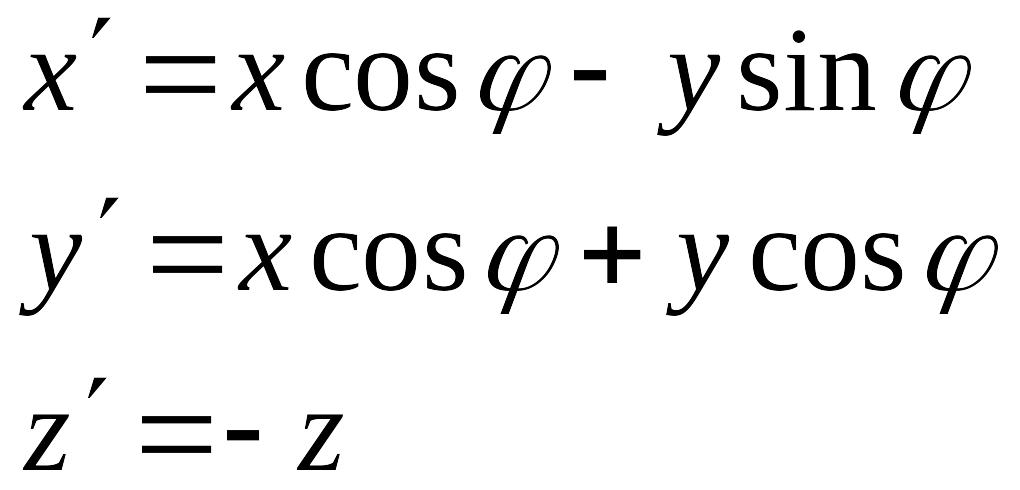
2
 )
скользящая симметрия (отражение
относительно некоторой плоскости
)
скользящая симметрия (отражение
относительно некоторой плоскости
![]() и сдвиг на вектор, параллельный
)
и сдвиг на вектор, параллельный
)
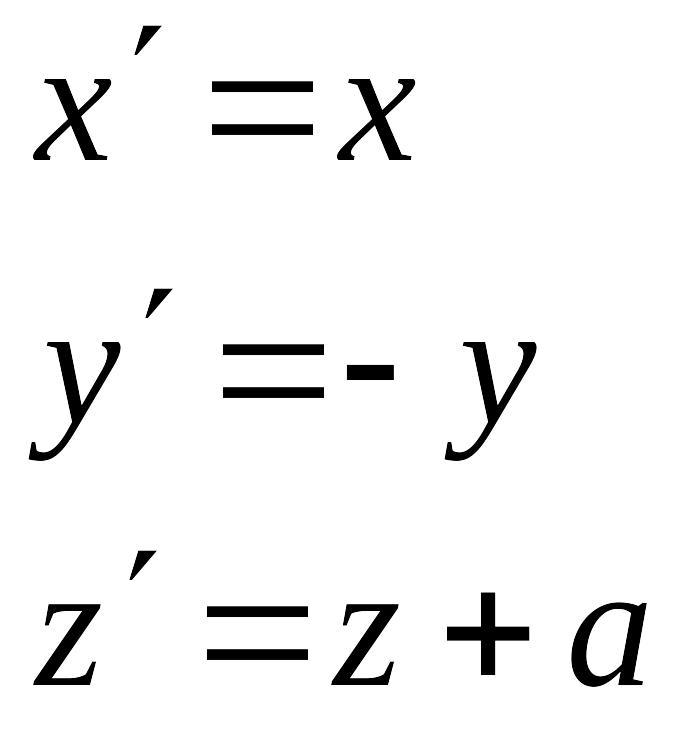


Теорема.
Любое собственное движение
![]() трёхмерного евклидового пространства
является винтовым движением. Любое
несобственное движение
трёхмерного евклидового пространства
является винтовым движением. Любое
несобственное движение
![]() является либо вращением с отражением,
либо скользящей симметрией.
является либо вращением с отражением,
либо скользящей симметрией.
Пусть
![]() -
евклидово пространство,
-
евклидово пространство,
![]() ,
-
движение. В
существует ортонормированный базис
,
-
движение. В
существует ортонормированный базис
![]() ,
,![]() ,
,![]() ,
канонический для
.
Зафиксируем начало координат – точку
,
канонический для
.
Зафиксируем начало координат – точку
![]() .
Тогда
.
Тогда
1)
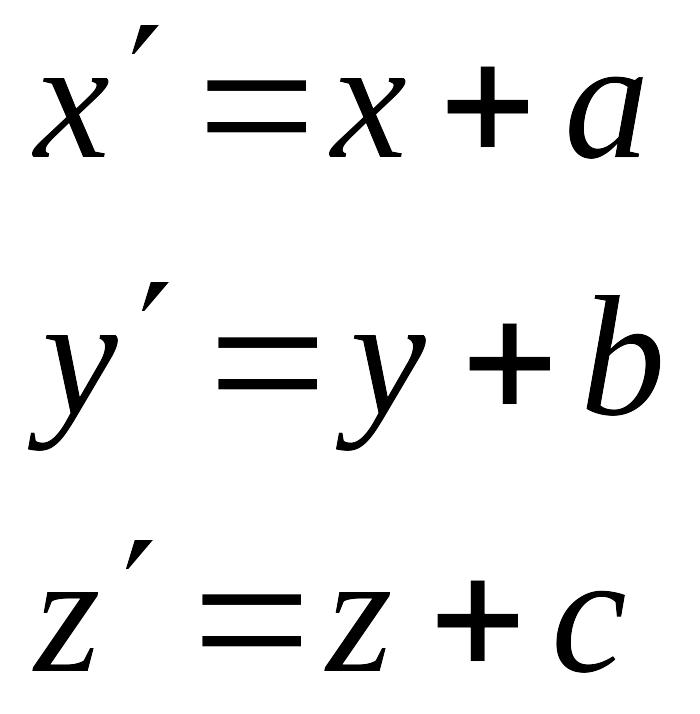 или 2)
или 2)
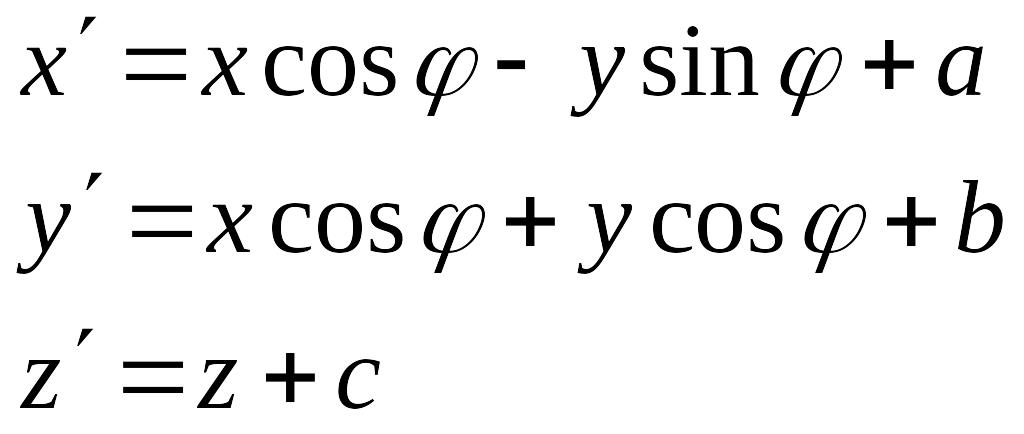 или 3)
или 3)
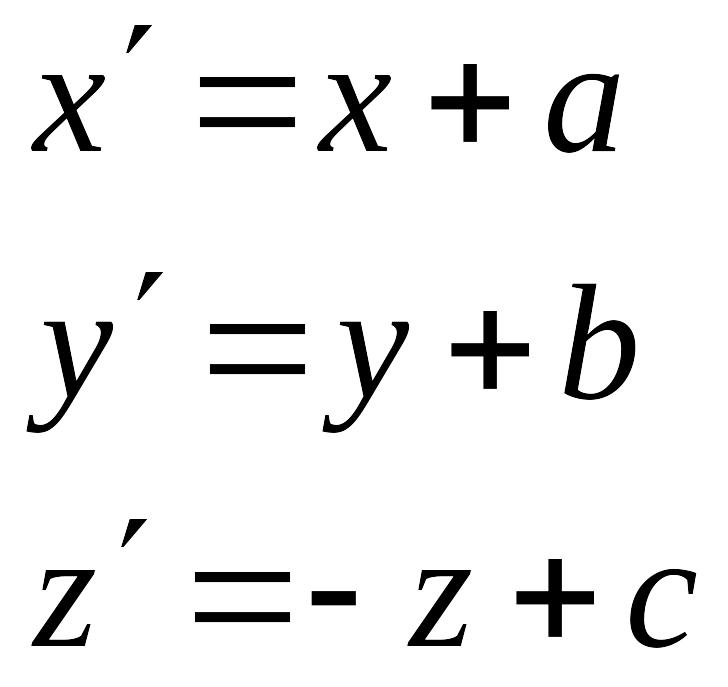 или 4)
или 4)
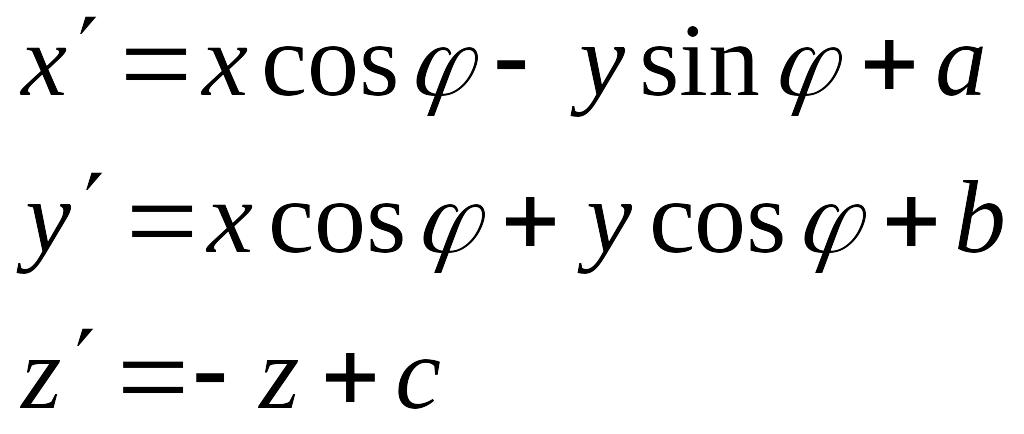
Случай 1
![]() ,
,
![]()
Случай 2
Как
и при n=2 находим
![]() такие, что
такие, что
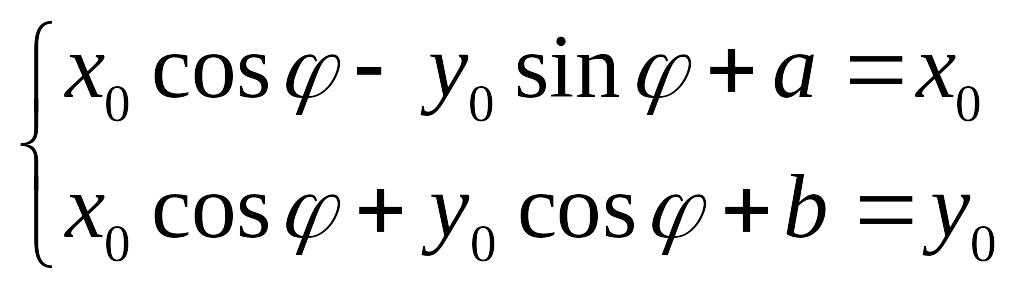
Тогда
после переноса начала координат в точку
![]() имеем
имеем
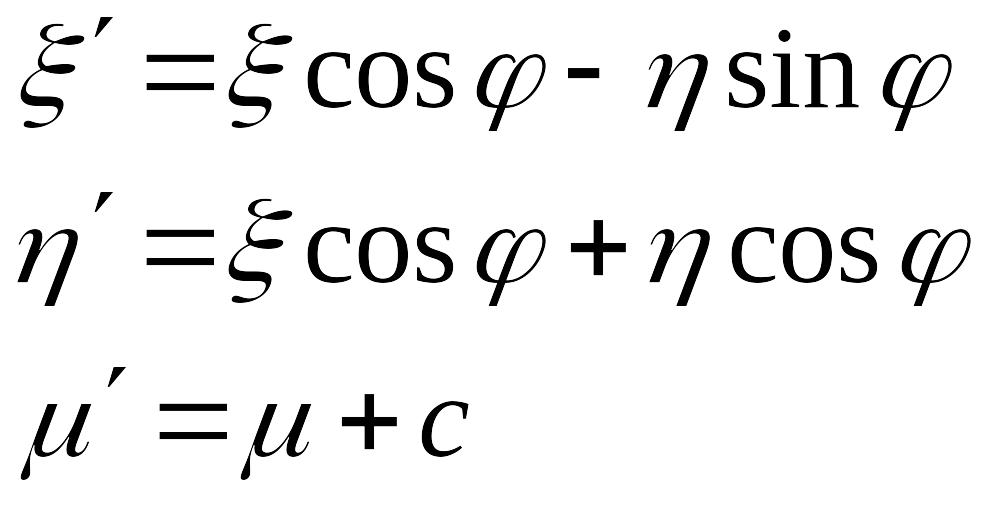
в новых координатах. Т.е. - винтовое движение.
Случай 3
Вводим
новые координаты:
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
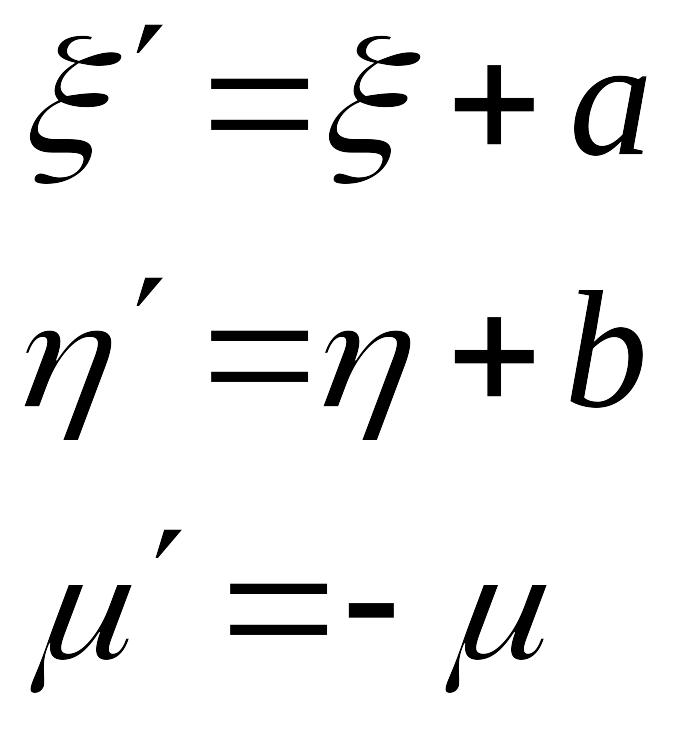
т.е.
это сдвиг на вектор
![]() и отражение относительно плоскости
и отражение относительно плоскости
![]() .
.
Случай 4
Ищем
точку
![]() ,
,![]() ,
,![]() как решение системы
как решение системы
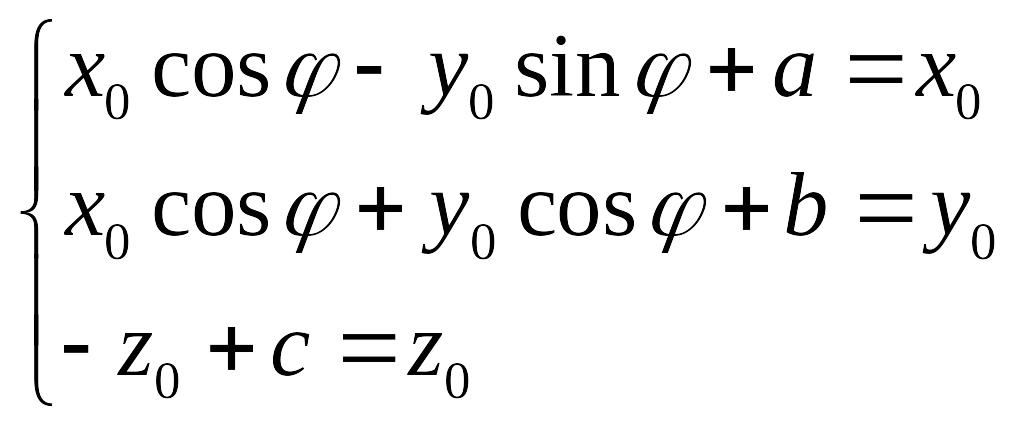
Это
возможно, т.к. матрица
![]() невырождена
невырождена
![]() .
.
Переносим
начало координат в точку
![]() ,
получаем
,
получаем
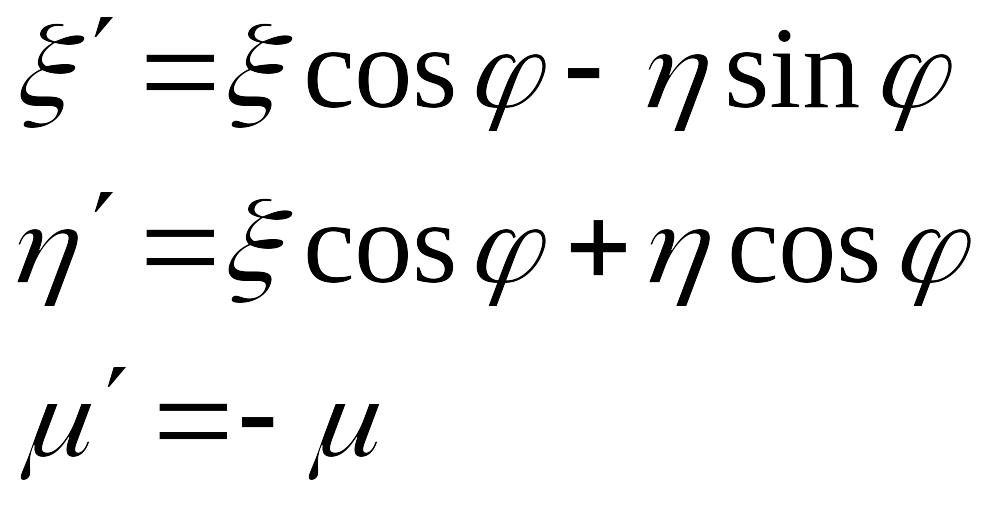
В
новых координатах это поворот в плоскости
![]() с отражением относительно этой плоскости.
с отражением относительно этой плоскости.

