
- •Зайцев м. В. Лекции по линейной алгебре.
- •1. Определения.
- •2. Линейная зависимость.
- •4. Матрицы перехода от базиса к базису.
- •5. Координаты в различных базисах.
- •6. Изоморфизм векторных пространств.
- •Подпространство
- •1. Определение.
- •2. Линейная оболочка.
- •3. Сумма и пересечение двух подпространств.
- •4. Прямая сумма подпространств.
- •Линейные и сопряженные пространства
- •1. Определение.
- •2. Определение.
- •Линейные отображения и операторы
- •1. Линейные отображения.
- •2. Задание линейных отображений матрицами.
- •Характеристический многочлен оператора
- •1. Определения
- •2. Геометрическая и алгебраическая кратность.
- •3. Спектр оператора
- •4. Диагонализируемые операторы
- •5. Минимальный многочлен оператора
- •6. Теорема Гамильтона-Кэли
- •Жорданова нормальная форма
- •1. Корневое подпространство
- •Нильпотентные операторы
- •3. Разложение в сумму корневых подпространств
- •4. Нормальный базис для нильпотентного оператора
- •5. Жордановы матрицы
- •6. Единственность жнф
- •1. Определение.
- •2. Матрица билинейной формы.
- •3. Изменение матрицы билинейной формы при замене базиса.
- •4. Симметрические и кососимметрические билинейные формы.
- •5. Канонический базис для симметрической билинейной формы.
- •6. Квадратичные формы
- •7. Алгоритм Лагранжа (приведения к каноническому виду).
- •8. Вещественные квадратичные формы
- •9. Теорема Якоби.
- •10. Положительно определенные квадратичные формы.
- •11. Канонический вид кососимметричной бф
- •Евклидовы пространства
- •3. Угол между векторами
- •4. Ортогональные векторы
- •5. Изоморфизм евклидовых пространств
- •6. Процесс ортогонализации Грамма-Шмидта
- •6. Ортогональные дополнения
- •8. Сопряжённые операторы
- •9. Самосопряжённые операторы
- •10. Приведение квадратичной формы к главным осям.
- •Ортогональные операторы
- •1. Основные понятия
- •2. Канонический базис для ортогонального оператора.
- •3. Полярное разложение.
- •Унитарные пространства
- •1. Эрмитовы (полуторалинейные) формы.
- •2. (Эрмитово) скалярное произведение.
- •3. Ортогональность.
- •4. Унитарные и эрмитовы матрицы.
- •6. Сопряжённый оператор.
- •6. Эрмитовы операторы.
- •7. Унитарные операторы.
- •Аффинные точечные пространства
- •2. Изоморфизм
- •3. Координаты в аффинном пространстве.
- •4. Подпространства.
- •Евклидовы точечные пространства
- •1. Евклидова метрика.
- •2. Расстояние от точки до плоскости.
- •3. Расстояние между плоскостями.
- •Квадрики в аффинном пространстве
- •1. Квадратичные функции в аффинном пространстве
- •2. Координатная запись
- •3. Центральная точка
- •4. Нахождение центра
- •5. Приведение квадратичной функции к каноническому виду.
- •Тензоры
- •1. Основные понятия.
- •2. Интерпретация тензоров малых рангов.
- •3. Произведение тензоров.
- •4. Координаты тензоров.
- •5. Изменение координат тензора при замене базиса
- •6. Свёртки тензоров.
- •Кососимметричные тензоры
- •Тензорная алгебра векторного пространства
- •Внешняя алгебра векторного пространства (алгебра грассмана)
- •1. Внешнее умножение.
- •2. Ассоциативность внешнего произведения.
- •3. Базис внешней алгебры.
- •4. Связь с определителями
2. Канонический базис для ортогонального оператора.
Теорема. Пусть — ортогональный оператор в . Тогда существует ортонормированный базис, в котором матрица имеет вид:



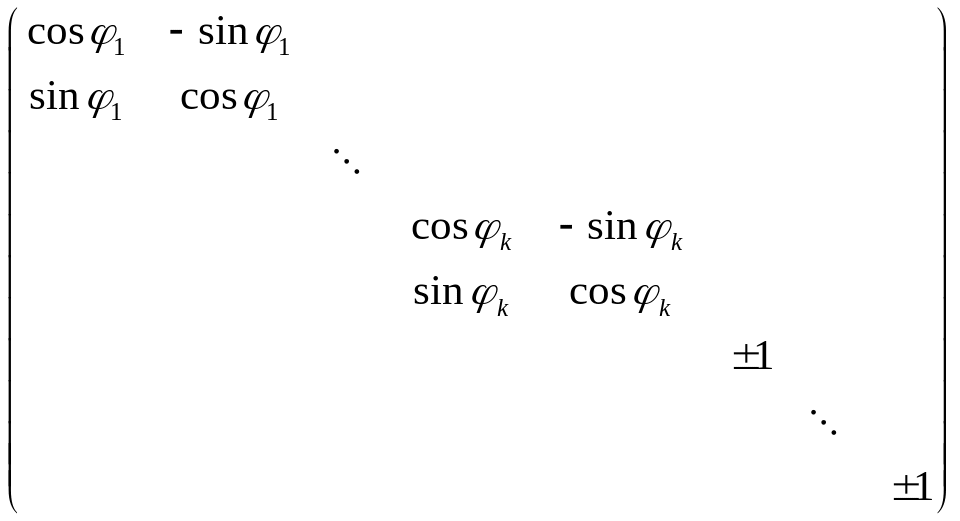
(1) По лемме 1 (см. самосопряжённые
операторы) у
есть инвариантное подпространство
![]() .
По лемме 5:
.
По лемме 5: ![]() .
Следовательно,
.
Следовательно,
![]() — инвариантные подпространства,
— инвариантные подпространства,
![]() или
или
![]() .
Кроме того,
.
Кроме того,
![]() не содержат инвариантных подпространств
не содержат инвариантных подпространств
![]() и
и
![]() .
При этом
.
При этом
![]() .
.
(2)
Пусть
![]() .
Тогда
.
Тогда
![]() и
и ![]() .
.
(3)
![]() ,
,
![]() — ортонормированный базис
,
— ортонормированный базис
,
 — матрица
в
этом базисе,
по лемме 4. Тогда
— матрица
в
этом базисе,
по лемме 4. Тогда
![]() .
.
(а)
Предположим, что
![]() .
Вычислим
.
Вычислим
![]() :
:
 .
Отсюда
.
Отсюда
![]() корни
корни
![]() на
— вещественные, следовательно, существует
собственный вектор в
в
есть 1-мерное
—
инвариантное подпространство.
Противоречие.
на
— вещественные, следовательно, существует
собственный вектор в
в
есть 1-мерное
—
инвариантное подпространство.
Противоречие.
(б)
остался случай
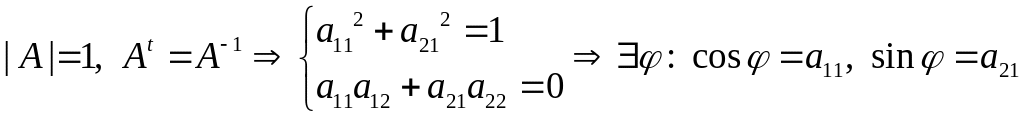 .
Тогда
.
Тогда
![]() ,
поэтому
,
поэтому
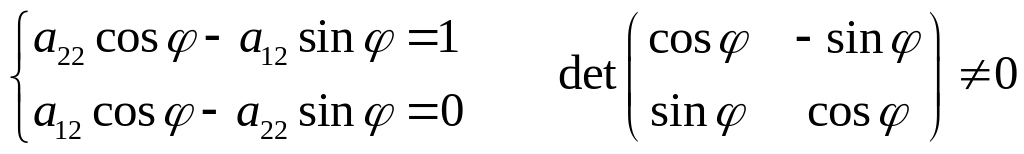 .
Значит, система имеет единственное
решение. Подходит
.
Значит, система имеет единственное
решение. Подходит
![]()
![]() .
.
3. Полярное разложение.
Теорема. Пусть
— невырожденный линейный оператор на
евклидовом пространстве
.
Тогда существуют ортогональный оператор
и самосопряжённый оператор
с положительными собственными значениями,
такие, что
![]() .
.
1)
Положим, что
![]() ,
где
*
- сопряжённый к
.
Тогда
,
где
*
- сопряжённый к
.
Тогда
![]() .
То есть
.
То есть
![]() самосопряжён.
самосопряжён.
2)
Существует ортонормированный базис, в
котором
имеет матрицу
![]() .
Пусть
.
Пусть
![]() — одно из собственных чисел
,
и
— собственный вектор. Тогда
— одно из собственных чисел
,
и
— собственный вектор. Тогда
![]()
![]() .
Отсюда и
.
Отсюда и
![]() ,
то есть все
,
то есть все
![]() — положительны.
— положительны.
3) Существует самосопряжённый оператор
с
матрицей
![]() в том же базисе. Ясно, что
в том же базисе. Ясно, что
![]() и
— невырожденный.
и
— невырожденный.
4)
Положим
![]() .
Тогда
.
Тогда
![]() так как
так как
![]() .
То есть
ортогонален.
.
То есть
ортогонален.
Тем самым мы доказали существование полярного разложения.
Унитарные пространства
1. Эрмитовы (полуторалинейные) формы.
Пусть
—
линейное пространство над![]() .
.
Определение.
— эрмитова форма на
,
если ![]() ,
причём:
,
причём:
1)
![]()
2)
![]() (комплексное сопряжение).
(комплексное сопряжение).
Следствие
1.
![]() .
.
Следствие
2.
![]() .
.
Следствие
3. ![]() .
.
Следствие
4.
![]() .
.
2. (Эрмитово) скалярное произведение.
Пусть — комплексное пространство.
Определение. Скалярное произведение
на
—
эрмитова положительно определённая
форма. Обозначение:
.
Положительная определённость:
![]() из
.
из
.
3. Ортогональность.
Пусть — унитарное пространство, то есть комплексное пространство со скалярным произведением.
Определение.
и
ортогональны, если
![]() .
.
Теорема. В конечномерном унитарном
пространстве можно выбрать ортонормированный
базис, т.е.
![]() .
.
Пусть
— произвольный базис
.
Возьмём любой
![]() .
Умножая на (вещественный) скаляр, можно
считать
.
Умножая на (вещественный) скаляр, можно
считать
![]() .
Пусть теперь
.
Пусть теперь
![]() .
Тогда
.
Тогда
![]() — уравнения с
неизвестными
— уравнения с
неизвестными
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() — подпространство в
,
— подпространство в
,
![]() .
По индукции (
.
По индукции (![]() )
в
есть ортонормированный базис
)
в
есть ортонормированный базис
![]() .
Положив,
.
Положив,
![]() ,
получаем ортонормированный базис
в
.
,
получаем ортонормированный базис
в
.
4. Унитарные и эрмитовы матрицы.
Пусть
— комплексная матрица
![]() .
.
Обозначим:
![]() (
(
![]() —
комплексное сопряжение).
—
комплексное сопряжение).
Определение.
Матрица
— эрмитова, если
![]() .
.
Матрица
— унитарная, если
![]() .
.
Теорема. Пусть
![]() — матрица перехода от одного ортогонального
базиса к другому ортогональному базису.
Тогда
унитарна.
— матрица перехода от одного ортогонального
базиса к другому ортогональному базису.
Тогда
унитарна.
Пусть
![]() — матрица перехода от
— матрица перехода от
![]() к
к
![]() .
Если
.
Если
![]() ,
то
,
то
![]()
![]() .
Если
.
Если
![]() — элементы
— элементы
![]() -ого
столбца
,
то
-ого
столбца
,
то
![]() — элементы
-ой
строки у матрицы
— элементы
-ой
строки у матрицы
![]() .
.
Произведение
-ой
строки
на
![]() -ый
столбец
равно
-ый
столбец
равно
![]() .
Но это есть
.
Но это есть
![]() ,
так как
,
так как
![]() .
Поэтому
.
Поэтому
![]() ,
так как базис
ортонормирован. Следовательно,
,
так как базис
ортонормирован. Следовательно,
![]() и
— унитарная матрица.
и
— унитарная матрица.
