
- •Зайцев м. В. Лекции по линейной алгебре.
- •1. Определения.
- •2. Линейная зависимость.
- •4. Матрицы перехода от базиса к базису.
- •5. Координаты в различных базисах.
- •6. Изоморфизм векторных пространств.
- •Подпространство
- •1. Определение.
- •2. Линейная оболочка.
- •3. Сумма и пересечение двух подпространств.
- •4. Прямая сумма подпространств.
- •Линейные и сопряженные пространства
- •1. Определение.
- •2. Определение.
- •Линейные отображения и операторы
- •1. Линейные отображения.
- •2. Задание линейных отображений матрицами.
- •Характеристический многочлен оператора
- •1. Определения
- •2. Геометрическая и алгебраическая кратность.
- •3. Спектр оператора
- •4. Диагонализируемые операторы
- •5. Минимальный многочлен оператора
- •6. Теорема Гамильтона-Кэли
- •Жорданова нормальная форма
- •1. Корневое подпространство
- •Нильпотентные операторы
- •3. Разложение в сумму корневых подпространств
- •4. Нормальный базис для нильпотентного оператора
- •5. Жордановы матрицы
- •6. Единственность жнф
- •1. Определение.
- •2. Матрица билинейной формы.
- •3. Изменение матрицы билинейной формы при замене базиса.
- •4. Симметрические и кососимметрические билинейные формы.
- •5. Канонический базис для симметрической билинейной формы.
- •6. Квадратичные формы
- •7. Алгоритм Лагранжа (приведения к каноническому виду).
- •8. Вещественные квадратичные формы
- •9. Теорема Якоби.
- •10. Положительно определенные квадратичные формы.
- •11. Канонический вид кососимметричной бф
- •Евклидовы пространства
- •3. Угол между векторами
- •4. Ортогональные векторы
- •5. Изоморфизм евклидовых пространств
- •6. Процесс ортогонализации Грамма-Шмидта
- •6. Ортогональные дополнения
- •8. Сопряжённые операторы
- •9. Самосопряжённые операторы
- •10. Приведение квадратичной формы к главным осям.
- •Ортогональные операторы
- •1. Основные понятия
- •2. Канонический базис для ортогонального оператора.
- •3. Полярное разложение.
- •Унитарные пространства
- •1. Эрмитовы (полуторалинейные) формы.
- •2. (Эрмитово) скалярное произведение.
- •3. Ортогональность.
- •4. Унитарные и эрмитовы матрицы.
- •6. Сопряжённый оператор.
- •6. Эрмитовы операторы.
- •7. Унитарные операторы.
- •Аффинные точечные пространства
- •2. Изоморфизм
- •3. Координаты в аффинном пространстве.
- •4. Подпространства.
- •Евклидовы точечные пространства
- •1. Евклидова метрика.
- •2. Расстояние от точки до плоскости.
- •3. Расстояние между плоскостями.
- •Квадрики в аффинном пространстве
- •1. Квадратичные функции в аффинном пространстве
- •2. Координатная запись
- •3. Центральная точка
- •4. Нахождение центра
- •5. Приведение квадратичной функции к каноническому виду.
- •Тензоры
- •1. Основные понятия.
- •2. Интерпретация тензоров малых рангов.
- •3. Произведение тензоров.
- •4. Координаты тензоров.
- •5. Изменение координат тензора при замене базиса
- •6. Свёртки тензоров.
- •Кососимметричные тензоры
- •Тензорная алгебра векторного пространства
- •Внешняя алгебра векторного пространства (алгебра грассмана)
- •1. Внешнее умножение.
- •2. Ассоциативность внешнего произведения.
- •3. Базис внешней алгебры.
- •4. Связь с определителями
Евклидовы пространства
1.
Пусть
-
векторное пространство над
![]()
Опр. Симметрическая билинейная
функция
-
скалярное произведение, если она
положительно определена. Т.е. если вести
обозначение
![]() :
:
2. Опр. Евклидово пространство
- векторное пространство над ![]() с
заданным на нем скалярным произведением
с
заданным на нем скалярным произведением
![]()
Опр. Матрица Грамма – на ij-том
месте стоит
![]() ,
где
,
где
![]() - вектора базиса Евклидова пространства.
- вектора базиса Евклидова пространства.
Опр. Длина (норма) вектора:
![]()
Свойства:
![]()
![]()
Теорема. (неравенство Коши -
Буняковского)
![]()
![]() при
всех
при
всех
![]() дискриминант
дискриминант
![]() уравнения
уравнения
![]() отрицателен
или равен нулю, где
отрицателен
или равен нулю, где
![]() .
Но
.
Но
![]()
![]()
Следствие 1. (неравенство треугольника)
![]()
![]()
Следствие 2.
![]()
3. Угол между векторами
Существует единственный угол
![]() такой, что
такой, что
![]()
Это угол между
![]() и
и
![]() .
.
![]()
4. Ортогональные векторы
Опр.
![]() и
и![]() ортогональны,
ортогональны,
![]() ,
если
,
если
![]()
Следствие 1. (теорема Пифагора)
![]()
Следствие 2. Диагонали ромба перпендикулярны
![]()
![]()
![]()
![]()
Опр.
-
ортогональный базис
,
если
![]() .
- ортонормированный, если он
ортогональный и
.
- ортонормированный, если он
ортогональный и
![]()
Теорема. В любом конечномерном евклидовом пространстве существует ортонормированный базис.
Пусть
![]() - квадратичная форма на
.
Она невырождена и положительно определена,
следовательно, существует базис
,
в котором
,
т.е. матрица
- квадратичная форма на
.
Она невырождена и положительно определена,
следовательно, существует базис
,
в котором
,
т.е. матрица
![]() (и
соответствующая ей матрица скалярного
произведения) равна
(и
соответствующая ей матрица скалярного
произведения) равна
![]()
5. Изоморфизм евклидовых пространств
Пусть и - два евклидовых пространства
Опр.
![]() -
изоморфизм евклидовых пространств,
если:
-
изоморфизм евклидовых пространств,
если:
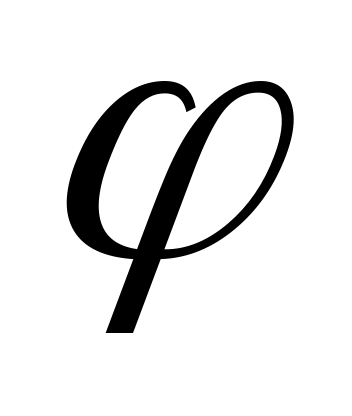 -
изоморфизм векторных пространств
-
изоморфизм векторных пространств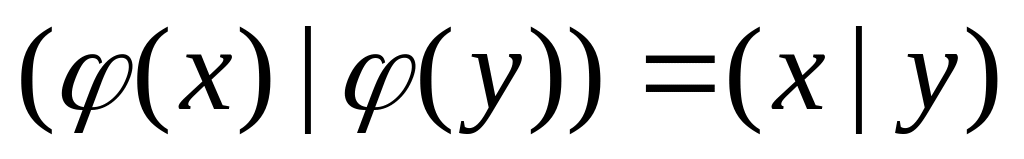
Теорема. Конечномерные евклидовы
пространства
и
изоморфны
тогда и только тогда, когда
![]()
Пусть
.
Рассмотрим ортонормированные базисы
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
Задаем отображение
:
.
Задаем отображение
:![]() .
Тогда
-
изоморфизм векторных пространств, и
.
Тогда
-
изоморфизм векторных пространств, и
![]()
Обозначение.
![]() -
n-мерное евклидово пространство.
-
n-мерное евклидово пространство.
6. Процесс ортогонализации Грамма-Шмидта
Теорема. Пусть
![]() - линейно независимые вектора
.
Тогда существует ортонормированная
система
- линейно независимые вектора
.
Тогда существует ортонормированная
система
![]() такая, что
такая, что
![]() для любого
для любого
![]()
Будем действовать пошагово.
![]() :
:
![]() .
.
Пусть
![]() уже
построен. Тогда
уже
построен. Тогда
![]() для любого i. Положим
для любого i. Положим
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() .
Если
.
Если
![]() ,
то нормируем его.
,
то нормируем его.
Следствие. Любую ортонормированную систему векторов в можно дополнить до ортонормированного базиса.
6. Ортогональные дополнения
Опр.
![]()
Свойство 1:
![]() - подпространство
- подпространство
Свойство 2:
![]()
Теорема. Пусть
-
конечномерное евклидово пространство.
Тогда для любого подпространства
выполнено
равенство:
![]()
Если
![]() ,
то
,
то
![]() и
не
пересекаются
и
не
пересекаются
![]() .
Пусть
-
ортонормированный базис
и
.
Пусть
-
ортонормированный базис
и
![]() .
Положим
.
Положим
![]() ,
и
,
и
![]() .
Тогда
.
Тогда
![]()
![]() ,
т.е.
,
т.е.
![]() и
и
![]()
![]()
Следствие.
![]() .
Если
,
то
.
Если
,
то
![]()
8. Сопряжённые операторы
Пусть
— евклидово пространство,
![]()
![]() .
.
Опр.
![]() сопряжён к
(обозначается
сопряжён к
(обозначается
![]() ),
если
),
если
![]() .
.
Таким
образом, по определению
![]() .
Существование для любого оператора
сопряжённого, докажем чуть позже.
.
Существование для любого оператора
сопряжённого, докажем чуть позже.
Предложение.
![]() и
и
![]()
(1).
![]()
![]() а значит, по предыдущей теореме
а значит, по предыдущей теореме
![]() .
.
(2).
![]() .
.
Теорема.
Пусть
— матрица оператора
![]() в ортонормированном базисе
в ортонормированном базисе
![]() .
Тогда
.
Тогда
![]() имеет
в этом базисе матрицу
имеет
в этом базисе матрицу
![]() .
.
Обозначим
![]() .
Пусть
— матрица
.
Пусть
— матрица
![]() в базисе
.
Тогда:
в базисе
.
Тогда:
![]() ,
,
![]() .
Непосредственно из определения и
ортонормированности базиса следует,
что
.
Непосредственно из определения и
ортонормированности базиса следует,
что
![]() .
Итак, доказано, что
.
Итак, доказано, что
![]() .
.
Замечание. Мы ещё не доказали существование сопряжённого оператора для любого, но это очевидно (достаточно положить = и провести аналогичное доказательство).
