4) Интегрирование тригонометрических функций

Интегралы вида

находятся с помощью тригонометрических формул

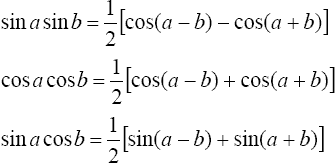
 Интегралы вида

где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

Примеры:

Найти неопределенный интеграл.

Используем формулу:

5)Понятие о неберущихся интегралах

 интеграл   не берётся, если функция   не является элементарной.

  1.   2.   3.   4.  5.   6.  7.   8.     9.   10. 

§ 3 Определённый интеграл Ньютона. Свойства.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо равенство  .

1. 

2.  где k - константа;

3. 

4. 

5. Если   для всех  , то  .

6. 

7. 

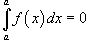
8. Если   в интервале [a, b], то 

§ 4 Определённый интеграл Римана.

1. Интегральная сумма Римана.

Пусть на отрезке   определена  функция f.

Рассмотрим разбиение отрезка   — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок   на n отрезков  . Длина наибольшего из отрезков  , где  , называется диаметром разбиения.

Отметим на каждом отрезке разбиения по точке  . Интегральной суммой называется выражение  .

Если при стремлении диаметра разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора  , то это число называется интегралом функции f на отрезке  , т.е. 

В этом случае, сама функция   называется интегрируемой (по Риману) на  ; в противном случае  является неинтегрируемой (по Риману) на отрезке  .

Геометрический смысл.

Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.

Суммы Дарбу и их свойства.

Функция y=f(x) определена на [a,b] и τ={xi}i=ki=0 некоторое его разбиение, Δxi=xi−x,i−1i=1,k.Sτ=Sτ(f)=∑ki=1MiΔxi=∑ki=1supf(x)xi−1<x<xi - верхняя сумма Дарбу, sτ=sτ(f)=∑ki=1miΔxi=∑ki=1inff(x)xi−1<x<xi- нижняя сумма Дарбу. Очевидно sτ≤Sτ.  Свойства: 1. Если к имеющимся точкам разбиения отрезка [a,b] на промежутки добавить новые точки, то нижняя сумма Дарбу от этого может разве лишь возрасти, а верхняя сумма -- уменьшается. Т.е. если τ′-измельчение разбиения τ, то Sτ′≤Sτ, sτ′≥sτ. 2. Каждая нижняя сумма Дарбу не превосходит каждую из верхних сумм, даже отвечающих другому разбиению промежутка. 3. Суммы Римана и Дарбу связаны соотношением sτ≤στ≤Sτ.  4. Sτ−sτ=∑ki=1ωi(f)Δxi, где ωi(f)=supf(ξi)−inff(ξi)- колебание функции на [xi−1,xi]. I*=supτsτ− нижний интеграл Дарбу функции f на [a,b], I*=infSττ-  верхний интеграл Дарбу. Множество {sτ} нижних сумм Дарбу ограничено сверху хотя бы одной из верхних сумм Дарбу тогда оно имеет I*=supτsτ причем I*≤Sτ. Множество верхних сумм Дарбу {sτ}ограничено снизу, поэтому существует I*=infSττ, причем I*≤I*. Т.о. sτ≤I*≤I*≤Sτ.

Необходимое и достаточное условие интегрируемости.

Теорема. Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0 (2.1).  Это условие означает, для любого ε>0 существует δ(ε)>0, что для любого разбиения τ мелкости меньше, чем δ выполняется неравенство: ∣Sτ−sτ∣<ε (2.2). Т.к. sτ≤Sτ, то из (2.2) следует Sτ−sτ<ε.