3. Движение заряженных частиц в электрическом и магнитном полях Основные понятия, законы и формулы

3.1. Сила , действующая на заряд , движущийся со скоростью в магнитном поле с индукцией :

; ,

где – угол между векторами и .

3.2. Сила , действующая на заряд в электрическом поле напряженностью :

.

3.3. Полная электромагнитная сила, действующая на заряд (сила Лоренца):

.

Это выражение является универсальным: оно справедливо как для постоянных, так и для переменных электрических и магнитных полей, причем при любых значениях скорости заряда.

Направление магнитной силы определяется по правилу левой руки. Как следует из п. 3.1, всегда перпендикулярна векторам и . Поэтому она сообщает движущейся заряженной частице только нормальное ускорение, не изменяя ее скорости и, следовательно, не совершая работы.

В электрическом поле сила направлена вдоль линии напряженности для положительно заряженной частицы и противоположна направлению вектора для отрицательно заряженной частицы. Сила при перемещении частицы всегда (за исключением случая, когда ) совершает работу, равную изменению кинетической энергии частицы.

3.4. Траектории движения частицы в магнитном поле.

• Если угол между векторами и равен 0, тогда сила Лоренца 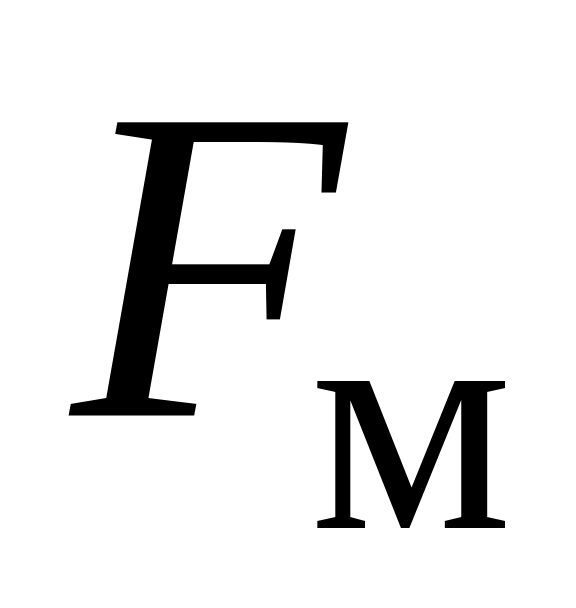равна нулю. Магнитное поле на частицу не действует, и она движется равномерно и прямолинейно.

• Если заряженная частица влетает в магнитное поле под углом 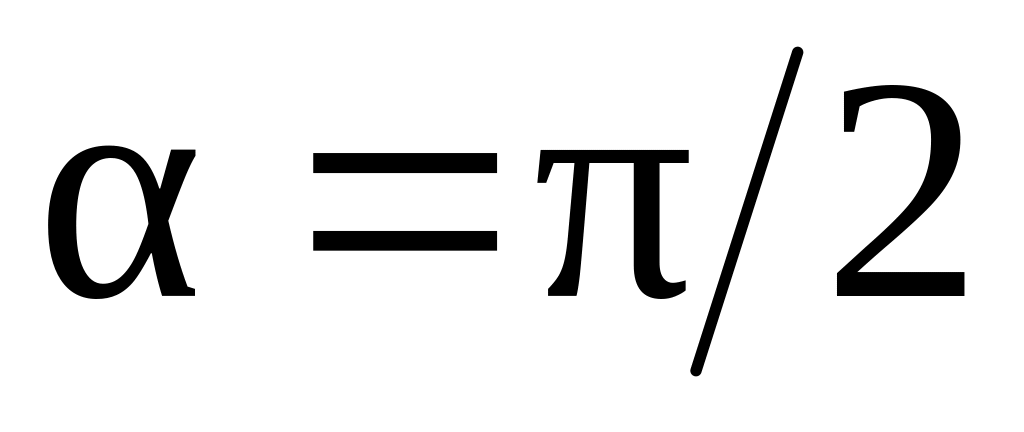, т.е. перпендикулярно вектору , тогда 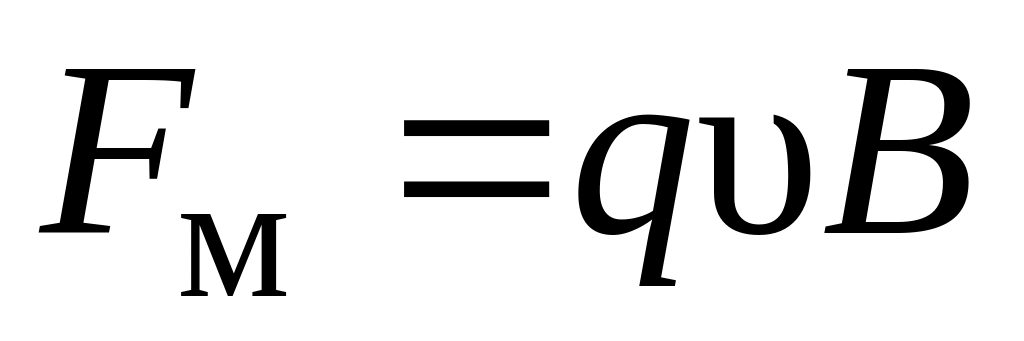постоянна по модулю, перпендикулярна скорости частицы и сообщает ей нормальное ускорение . Частица будет двигаться по окружности, радиус которой определяется из условия

,

откуда

.

Период вращения частицы не зависит от ее скорости:

.

• Если частица влетает в магнитное поле под углом к линиям вектора (рис. 7), то ее движение можно представить в виде суперпозиции:

1. р 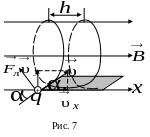авномерного прямолинейного движения вдоль линий магнитной индукции со скоростью ;

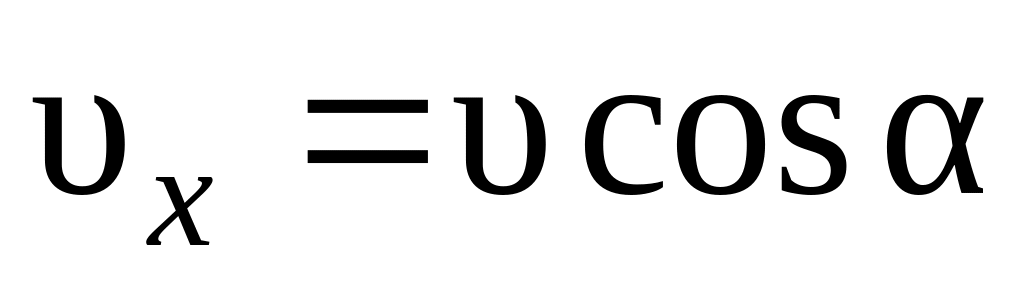2. равномерного движения со скоростью 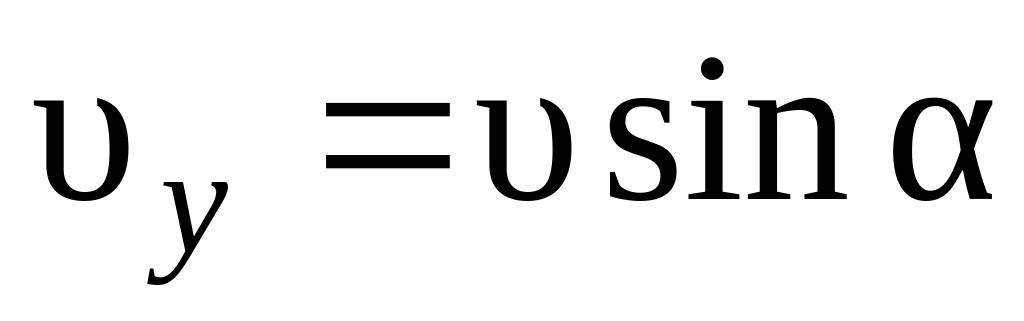по окружности в плоскости, перпендикулярной линиям магнитной индукции.

В результате частица будет двигаться по винтовой линии радиусом

и с шагом, равным пути, пройденному частицей вдоль поля со скоростью за время, которое понадобится частице для того, чтобы совершить один оборот:

4. Электромагнитная индукция Основные понятия, законы и формулы

4.1. Магнитный поток:

• в случае однородного магнитного поля и плоской поверхности

или ,

где – площадь контура, – угол между нормалью к плоскости контура и вектором магнитной индукции ; – проекция вектора на нормаль к поверхности контура :

• в случае неоднородного поля и производной поверхности

,

где интегрирование ведется по всей поверхности ; – вектор, направленный по нормали к поверхности, модуль которого равен площади элемента поверхности.

4.2. Теорема Гаусса для потока вектора :

поток вектора сквозь любую замкнутую поверхность равна нулю, т.е.

.

4.3. Работа по перемещению замкнутого контура с постоянным током в магнитном поле:

,

где – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.

4.4. Потокосцепление, т.е. полный поток, сцепленный со всеми витками системы (соленоида или тороида):

,

где – магнитный поток через один виток (считаем, что все витки одинаковой формы в одном и том же поле), – число витков.

Магнитный поток, создаваемый током в контуре:

,

где – индуктивность контура.

4.5. Индуктивность длинного соленоида с немагнитным сердечником:

,

где – число витков, приходящихся на единицу длины соленоида; – длина; – площадь поперечного сечения; – объем соленоида.

4.6. Основной закон электромагнитной индукции (закон Фарадея-Максвелла): при всевозможных изменениях магнитного потока, пронизывающего поверхность, натянутую на проводящий контур, в этом контуре возникает электродвижущая сила индукции, пропорциональная скорости изменения магнитного потока, взятой с обратным знаком:

.

4.7. Самоиндукция: возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока

.

Если контур не деформируется и магнитная проницаемость среды не меняется , тогда

.

4.8. Сила тока в цепи, обладающей постоянными сопротивлением и индуктивностью и содержащей постоянную э.д.с. , изменяется при замыкании и размыкании цепи по закону:

.

При замыкании цепи начальная сила тока , при размыкании .

4.9. Заряд, прошедший по контуру сопротивлением при изменении магнитного потока сквозь контур на величину за время :

,

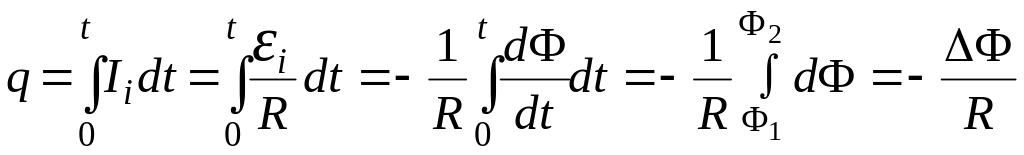где – индукционный ток в контуре .

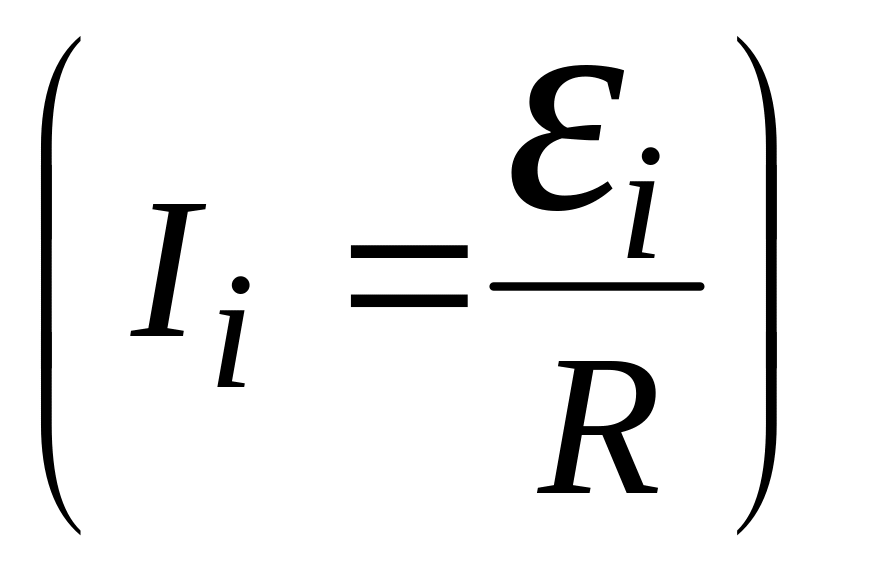4.10. Взаимная индукция: возникновение ЭДС в одном из двух близко расположенных друг к другу проводящих контуров при изменении силы тока в другом контуре.

Взаимная индуктивность двух катушек, находящихся на одном сердечнике в вакууме:

,

где и - число витков первой и второй катушек соответственно.