
- •§1 Неопределённый интеграл. Таблица интегралов.
- •3)Методы интегрирования:
- •§2 Интегрирование специальных функций
- •1)Интегрирование рациональных дробей
- •3)Дифференциальный бином
- •4) Интегрирование тригонометрических функций
- •§ 3 Определённый интеграл Ньютона. Свойства.
- •§ 4 Определённый интеграл Римана.
- •Необходимое условие интегрируемости функции
- •§ 5 Классы интегрируемых функций. Свойства определённого интеграла Римана.
- •§ 6 Приложение определенного интеграла Римана.
- •§ 7 Несобственные интегралы
4) Интегрирование тригонометрических функций
Интегралы вида
![]()
находятся с помощью тригонометрических формул
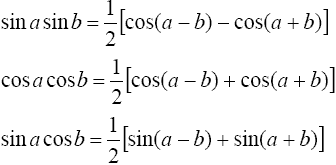
Интегралы вида
![]()
где m и n - четные числа находятся с помощью формул понижения степени
![]()
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
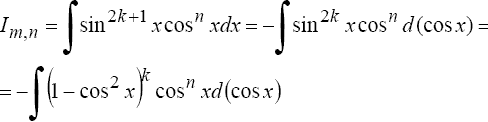
Примеры:
![]() Найти
неопределенный интеграл.
Найти
неопределенный интеграл.
![]()
Используем
формулу:
![]()

5)Понятие о неберущихся интегралах
интеграл ![]() не
берётся,
если функция
не
берётся,
если функция ![]() не
является элементарной.
не
является элементарной.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. 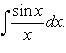 5.
5. 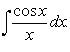 6.
6. ![]() 7.
7. 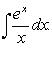 8.
8. 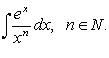 9.
9. 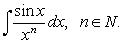 10.
10. 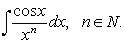
§ 3 Определённый интеграл Ньютона. Свойства.
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b] и F(x) -
одна из первообразных функции на этом
отрезке, тогда справедливо равенство ![]() .
.
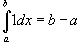
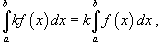 где k -
константа;
где k -
константа;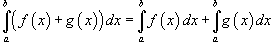
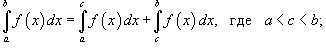
Если
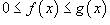 для
всех
для
всех 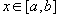 ,
то
,
то 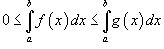 .
.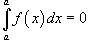
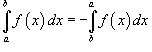
Если
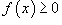 в
интервале [a,
b], то
в
интервале [a,
b], то 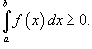
§ 4 Определённый интеграл Римана.
Интегральная сумма Римана.
Пусть
на отрезке ![]() определена
функция f.
определена
функция f.
Рассмотрим разбиение
отрезка ![]() —
конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок
на n отрезков
—
конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок
на n отрезков ![]() .
Длина наибольшего из отрезков
.
Длина наибольшего из отрезков ![]() ,
где
,
где ![]() ,
называется диаметром
разбиения.
,
называется диаметром
разбиения.
Отметим
на каждом отрезке разбиения по
точке ![]() . Интегральной
суммой называется
выражение
. Интегральной
суммой называется
выражение ![]() .
.
Если
при стремлении диаметра разбиения к
нулю интегральные суммы стремятся к
одному и тому же числу, независимо от
выбора
,
то это число называется интегралом функции f на
отрезке
,
т.е. ![]()
В
этом случае, сама функция ![]() называется интегрируемой
(по Риману) на
;
в противном случае
является неинтегрируемой
(по Риману) на
отрезке
.
называется интегрируемой
(по Риману) на
;
в противном случае
является неинтегрируемой
(по Риману) на
отрезке
.
Геометрический смысл.
Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.
Необходимое условие интегрируемости функции
Если функция f (x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке. Доказательство. Предположим обратное. Допустим, что f (x) является неограниченной на отрезке [a, b]. Покажем, что в этом случае интегральную сумму можно сделать сколь угодно большой за счет выбора точек ξ 1, ξ 2,…, ξ n при любом разбиении отрезка [a, b]. Действительно, так как f (x) не ограничена на [a, b], то при любом разбиении отрезка [a, b] она обладает этим свойством хотя бы на одном частичном отрезке разбиения, например на [x0, x1]. Выберем на остальных частях отрезка точки ξ 2, ξ 3,…, ξ n произвольно и обозначим
![]()
Зададим произвольное число М > 0 и возьмем такое ξ 1 на [x0, x1], чтобы
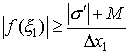 .
.
Это можно сделать в силу неограниченности функции f (x) на [x0, x1]. Тогда
![]() и
и ![]() ,
,
т.е. интегральная сумма σ по абсолютной величине может быть больше любого наперед заданного числа. Поэтому интегральная сумма σ не имеет конечного предела при λ → 0, а это означает, что определенный интеграл от неограниченной функции не существует. Замечание. Обратная теорема неверна, т.е. условие ограниченности функции f (x) необходимое, но не является достаточным условием интегрируемости функции.
Понятие верхней и нижней сумм
Пусть функция f(x) ограничена на сегменте [a, b] и T - разбиение этого сегмента точками a = x0 < x1 < ... < xn = b. Обозначим через Mi и miсоответственно точную верхнюю и точную нижнюю грани этой функции на сегменте [xi-1, xi]. Суммы
![]()
![]()
![]()
![]() и
и
![]()
![]()
![]()
![]()
называются соответственно верхней и нижней суммами функции f(x) для данного разбиения T сегмента [a, b].
Очевидно, что любая интегральная сумма I{xi, ξi} данного разбиения T сегмента [a, b] заключена между верхней и нижней суммами S и s этого разбиения.
Понятия верхней и нижней сумм становятся особенно ясными, если обратиться к геометрическим представлениям. Для простоты рассмотрим положительную и непрерывную функцию f(x) и криволинейную трапецию, определяемую этой функцией (см. Рис. 1. и Рис. 2.).
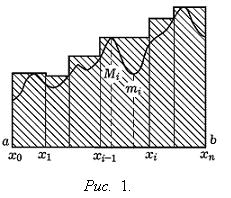

Если T -
некоторое разбиение сегмента [a, b],
то числа Mi и mi представляют
собой в случае непрерывной функции f(x)
максимальное и минимальное значения
этой функции на частичном сегменте
[xi-1, xi]
разбиения T.
Поэтому верхняя сумма S равна
площади, заштрихованной на Рис. 1.
ступенчатой фигуры, которая содержит
криволинейную трапецию, а нижняя
сумма s равна
площади, заштрихованной на Рис. 2.
ступенчатой фигуры, которая содержится
в криволинейной трапеции (эта трапеция
на рисунках 1 и 2 обведена жирной линией).
Обозначим
через ![]() точную
нижнюю грань множества {S}
верхних сумм, а через
точную
нижнюю грань множества {S}
верхних сумм, а через ![]() -
точную верхнюю грань множества нижних
сумм:
-
точную верхнюю грань множества нижних
сумм:
![]()
![]()
![]()
Числа и называются соответственно верхним и нижним интегралами Дарбу от функции f(x).
Критерий Дарбу интегрируемости функции
Приведенные утверждения даны для функции одной переменной.
Пусть
функция ![]() определена
и ограничена на отрезке
определена
и ограничена на отрезке ![]() .
Пусть
.
Пусть ![]() и
и ![]() -
верхний и нижний интегралы
Дарбу функции
на
заданном отрезке соответственно. Тогда
следующие 3 условия эквивалентны:
-
верхний и нижний интегралы
Дарбу функции
на
заданном отрезке соответственно. Тогда
следующие 3 условия эквивалентны:
интегрируема по Риману на отрезке ,
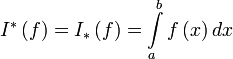 ,
,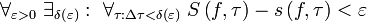 ,
где
,
где 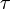 и
и  —
некоторое разбиение и его мелкость.
—
некоторое разбиение и его мелкость.Теорема о критерии сущ. интеграла по Риману
Для того чтобы ограниченная функция
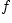 была
интегрируемой на отрезке
была
интегрируемой на отрезке 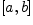 ,
необходимо и достаточно, чтобы для
любого
,
необходимо и достаточно, чтобы для
любого 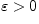 нашлось
такое разбиение
нашлось
такое разбиение 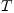 отрезка
,
при котором
отрезка
,
при котором 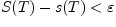
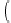 или
или 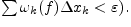
Теорема о среднем.
Если f(x)
- непрерывная функция, заданная на
промежутке [a, b],
то существует такая точка ![]()
![]() ,
что
,
что
![]()
![]() (14) В
самом деле, пусть M и m наибольшее
и наименьшее значения f(x)
на промежутке [a, b].
Составим для f(x)
какую-нибудь интегральную сумму
(14) В
самом деле, пусть M и m наибольшее
и наименьшее значения f(x)
на промежутке [a, b].
Составим для f(x)
какую-нибудь интегральную сумму
![]()
![]()
![]() Так
как при всех k будет m ≤ f(ξk)
≤ M,
а xk+1 > xk,
то m(xk+1 - xk)
≤ M(xk+1 - xk).
Складывая такие неравенства и замечая,
что
Так
как при всех k будет m ≤ f(ξk)
≤ M,
а xk+1 > xk,
то m(xk+1 - xk)
≤ M(xk+1 - xk).
Складывая такие неравенства и замечая,
что
![]()
![]()
![]() получим:m(b - a)
≤ σ ≤ M(b - a).
получим:m(b - a)
≤ σ ≤ M(b - a).
Переходя
в этом неравенстве к пределу при λ →
0, приходим после деления на b - a к
новому неравенству![]()
![]()
![]() Таким
образом, частное
Таким
образом, частное![]()
![]()
![]()
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14).
Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.
