Тема 3. Рекурсия Пример выполнения задания
Задание: С
помощью рекурсивной подпрограммы,
вычисляющей произведение n
сомножителей, вычислить
для = 0.00001.
Решение. В терминальной ситуации произведение равно первому сомножителю. Рекурсивная функция вычисляет произведение n сомножителей.
program Recurs_cosinus;
const e = 0.00001;
function proizv(x : real; n : word) : real;
begin {cos как произведение n сомножителей}
if n = 1 then proizv := 1- 4*x*x/pi/pi {сомножитель! при n=1}
else proizv := proizv(x, n-1)*(1- 4*x*x/sqr(2*n - 1)/pi/pi) end;
var
p1, p2, arg : real; n : word;
begin {cos с заданной погрешностью}
n := 2;
writeln('Введите аргумент'); readln(arg);
p1:= proizv(arg, n);
repeat
p2 := p1; n := n + 1;
p1 :=proizv(arg,n)
until abs(p1- p2) < e;
writeln('proizv = ', p1:8:6,' cos = ', cos(arg):8:6);
end.
Варианты задания
Выполнить свой вариант задания с использованием рекурсии.
Вывести первые 10 чисел Фибоначчи, если F(1)=1, F(2)=1, а F(n)=F(n-1)+F(n-2).
Вычислить значения первых пяти полиномов Лежандра для x=1:
,
,
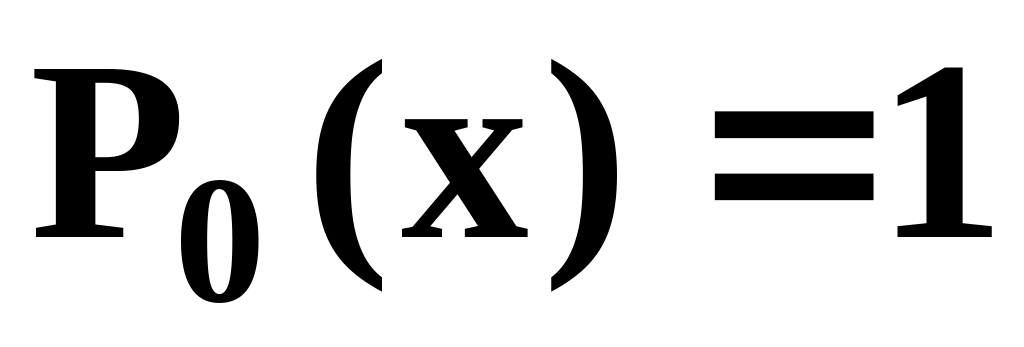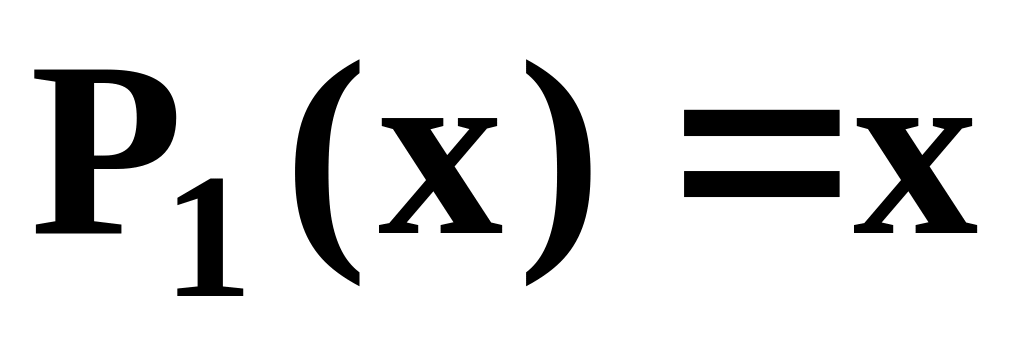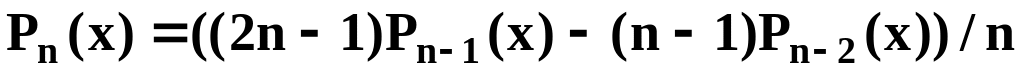.С погрешностью 0.001 уточнить методом деления отрезка пополам корень уравнения
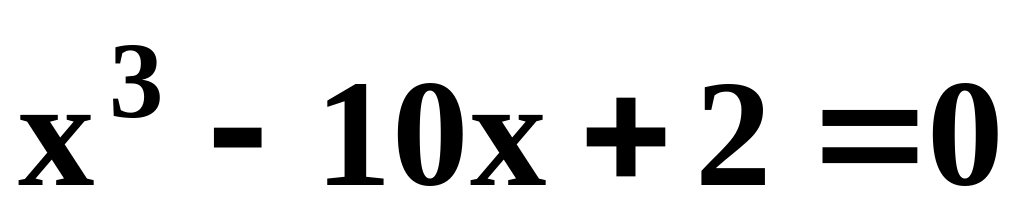на отрезке [0; 4].С погрешностью 0.001 уточнить по методу Ньютона корень уравнения ln(x) - x +1.8 = 0 на отрезке [2; 3].
Уточнить корень уравнения ln(x)- x +1.8 =0 на отрезке [2; 3] методом простой итерации с погрешностью 0.0001.
Вывести на экран геометрическую прогрессию от 1 до 10 с q = 1.3.
Извлечь с погрешностью 0.001 по методу Ньютона
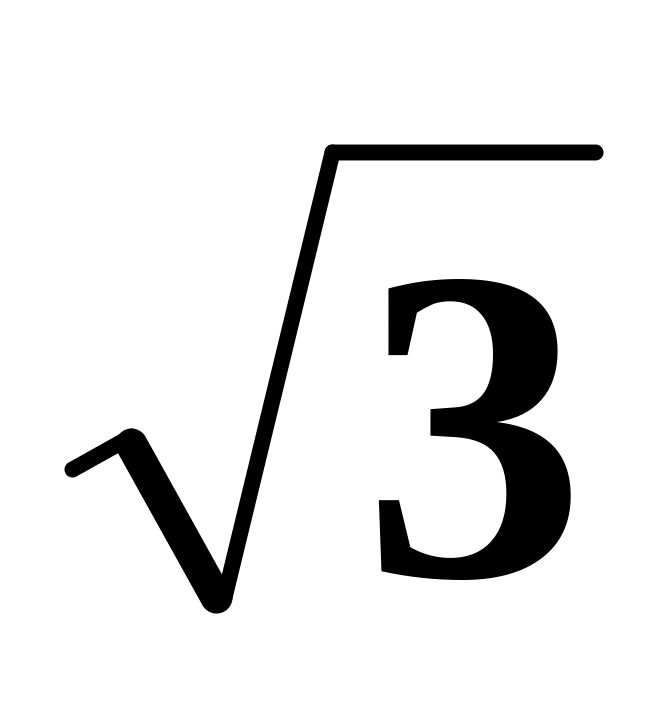и
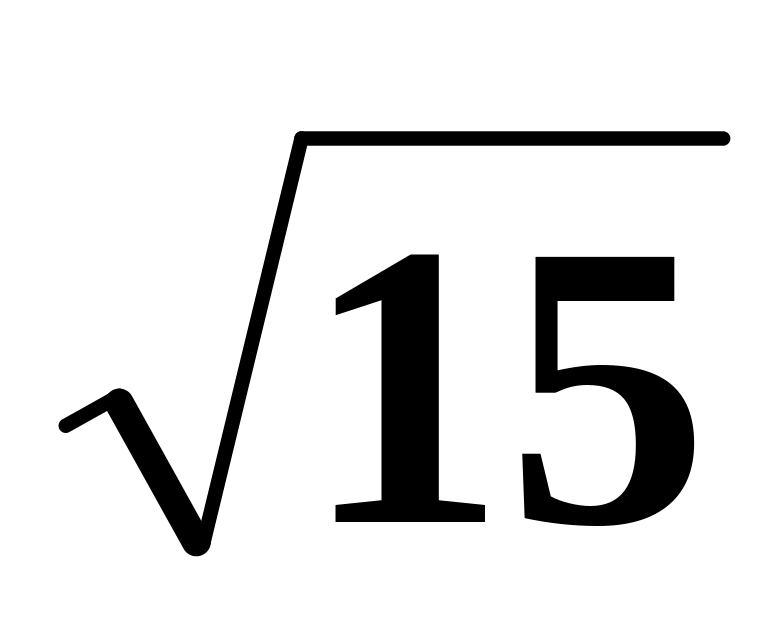.Вычислить 9! и 1!.
Методом прямоугольников вычислить с ε = 0.001
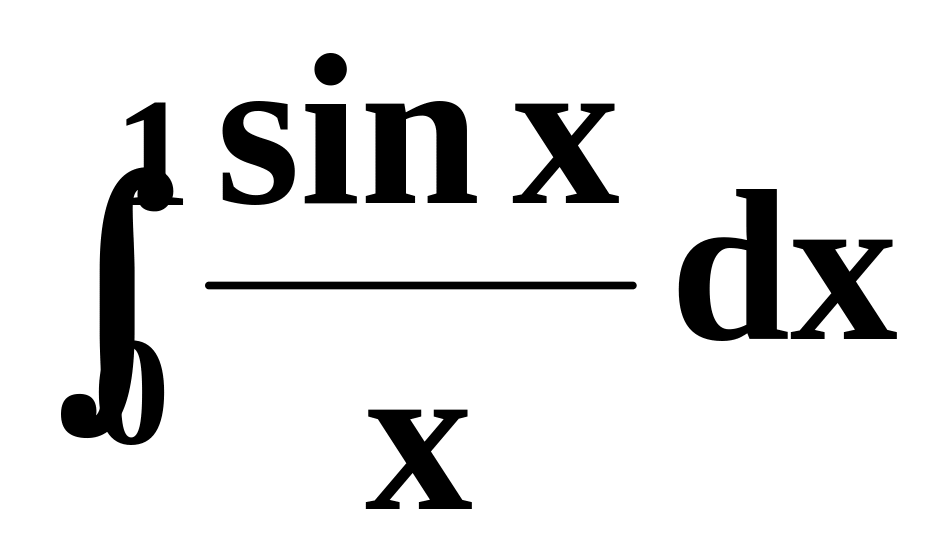.С погрешностью 0.001 вычислить
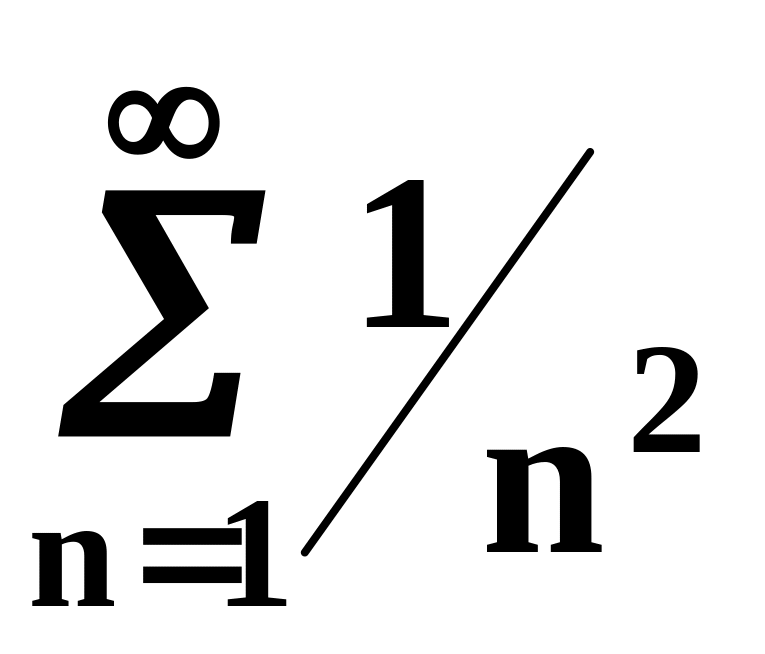.С погрешностью 0.001 вычислить
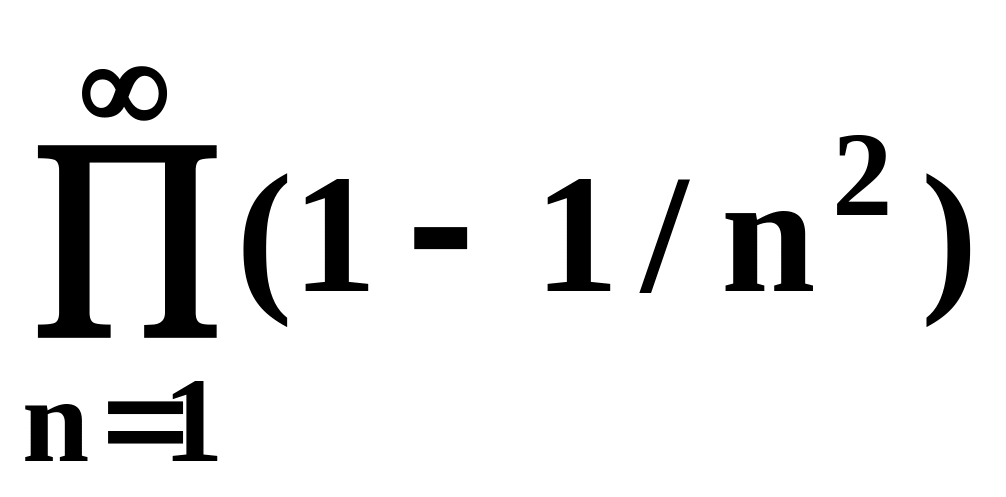.Вычислить
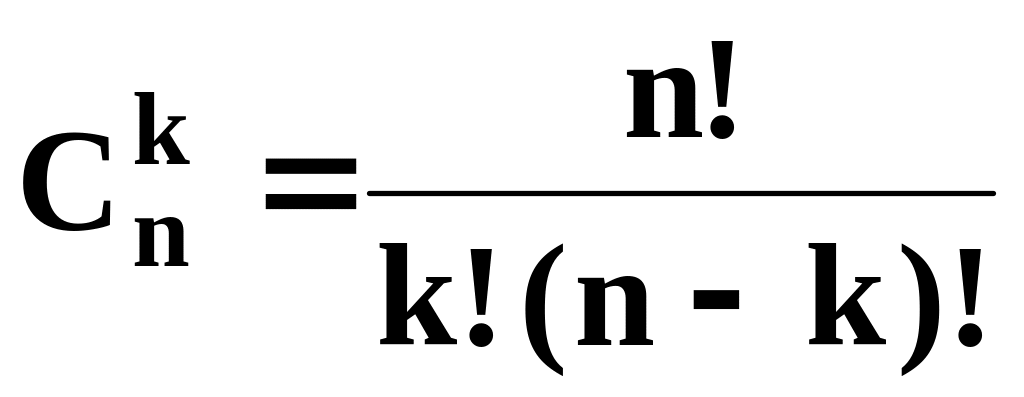для n=6, k=2
и n=8, k=3.Вычислить
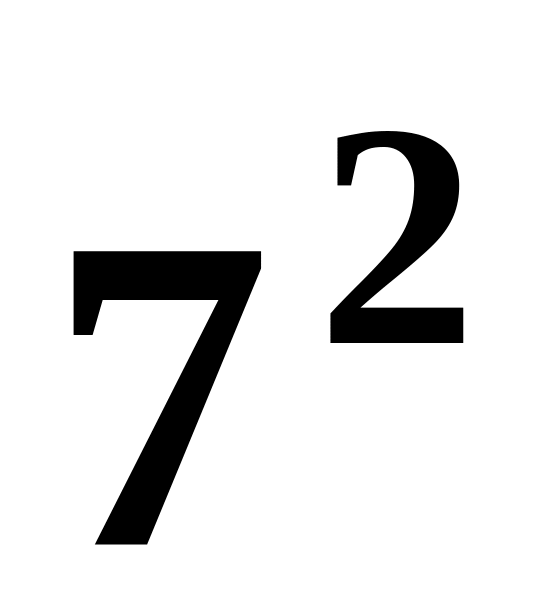и
,
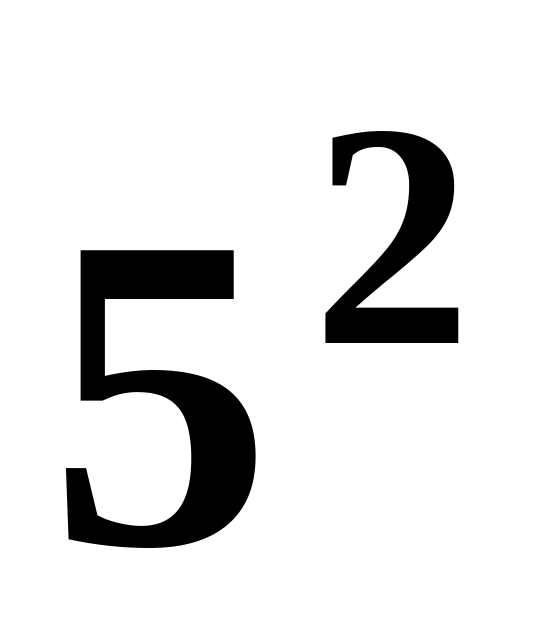используя представление квадратов
чисел:
,
,
,
,
…
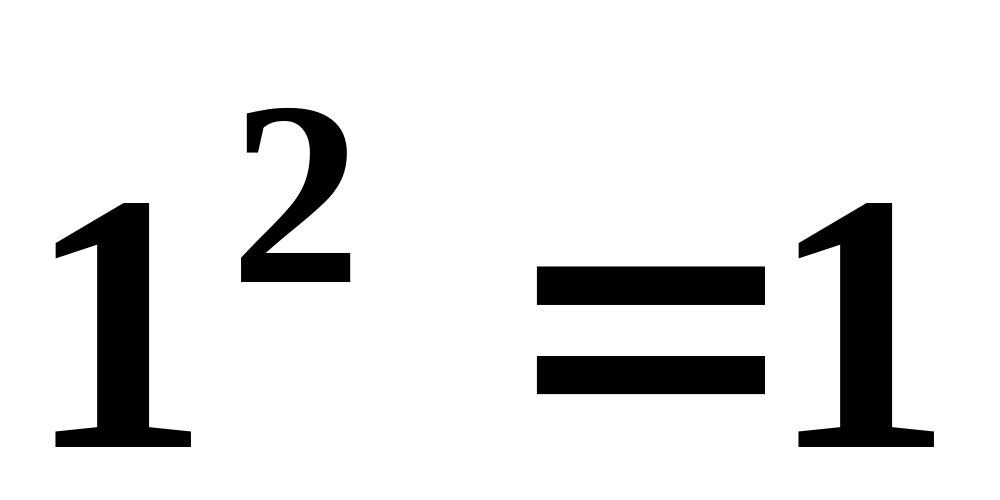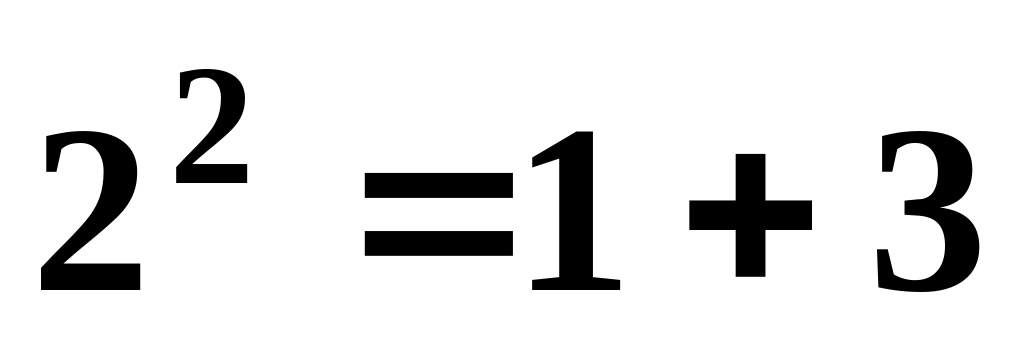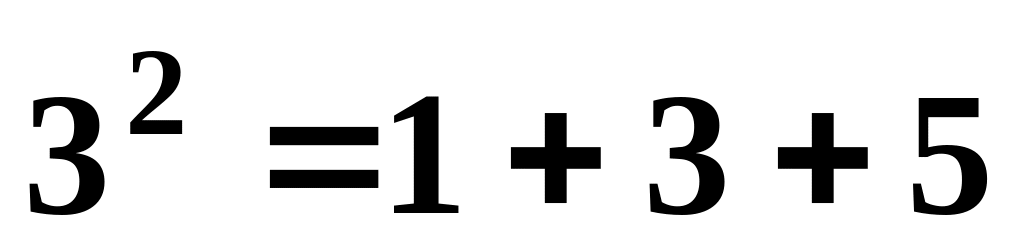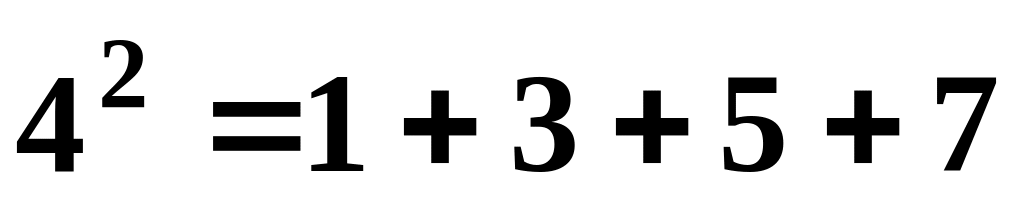.Среди целых чисел диапазона word найти числа, равные сумме факториалов его цифр (например, 145=1!+4!+5!).
Вычислить значения первых пяти многочленов Чебышева:
,
,
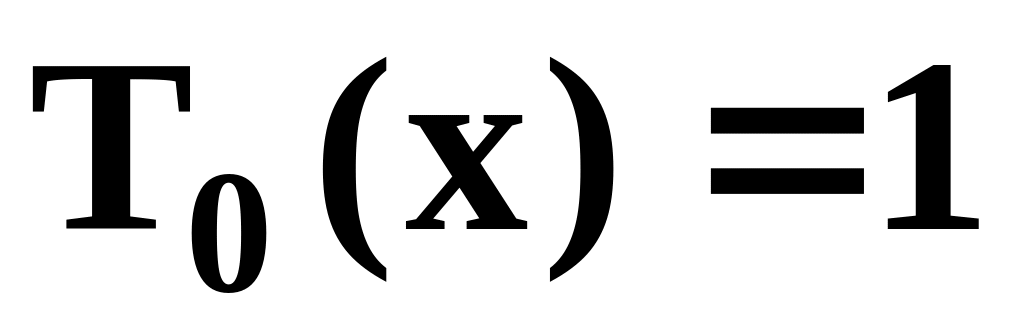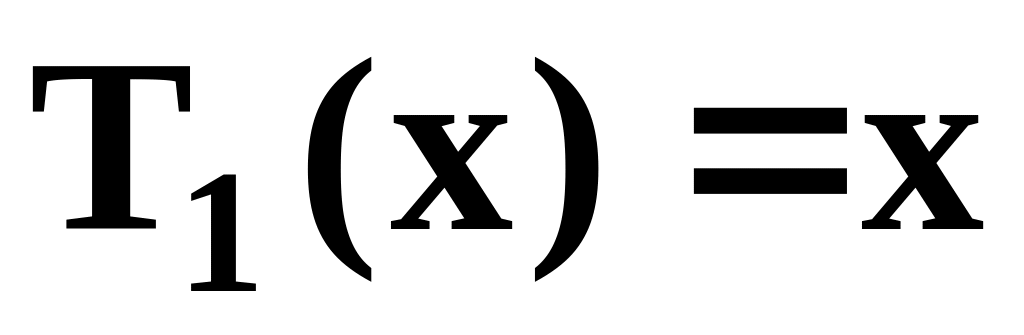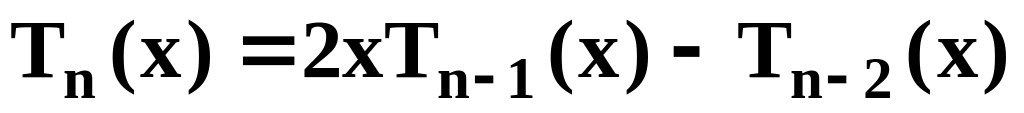для x=0.5.Создать две арифметические прогрессии из 10 элементов с начальными значениями 1.2 и 2.7 и шагом соответственно 0.7 и 0.35.
Вычислить p+(p+1)+(p+2)+…+(p+n) для p=0.7, n=10 и p=0.5, n=15.
С погрешностью 0.00001 вычислить e=1+1/1!+1/2!+1/3!+…+1/n!+… .
Вычислить для n=7 и n=10
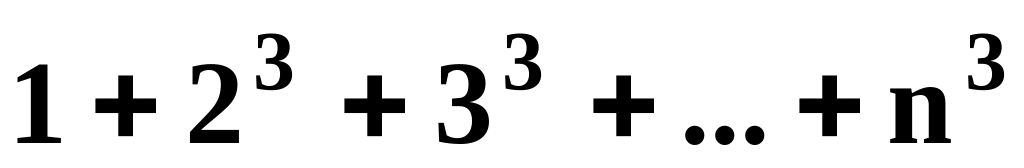.Вычислить 1/e = 1 - 1/1! + 1/2! - 1/3!+… с погрешностью 0.001.
Для x=0.8 вычислить значения первых 6 полиномов Эрмита:
,
,
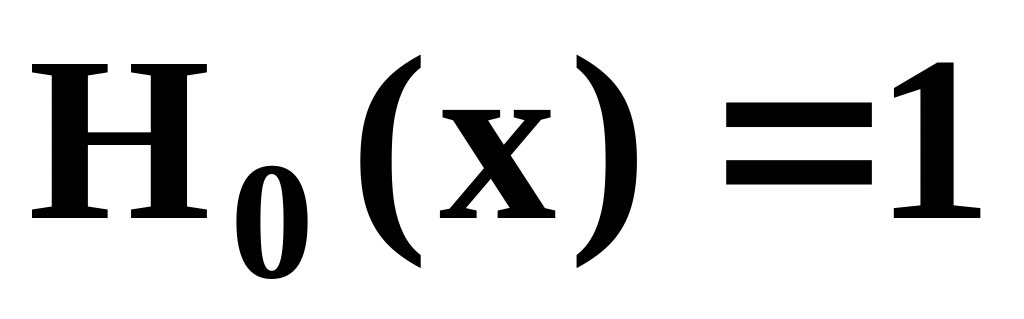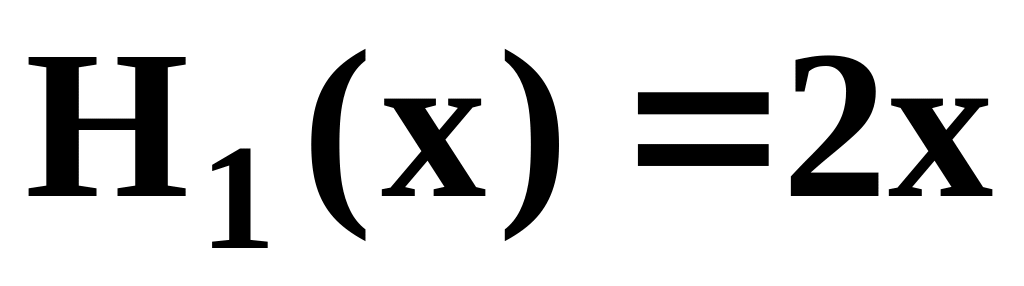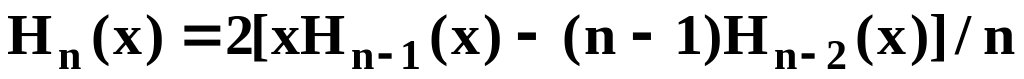.Для x=0.5 вычислить значения первых пяти полиномов Лагерра:
,
,
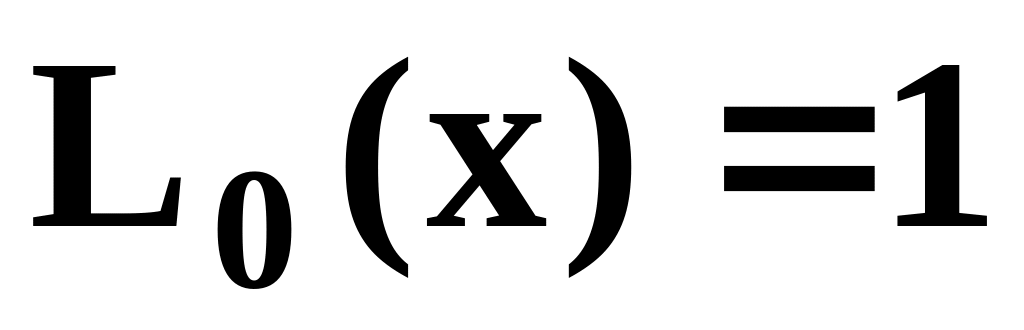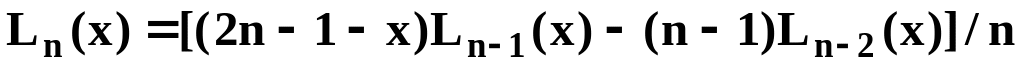.Осуществить перемножение двух целых чисел с представлением исходных данных и результата на экране в двоичной системе.
Подсчитать количество переносов колец ханойской башни с одного столба на другой. Можно переносить только по одному кольцу, класть меньшее на большее, используя третий столб. Исходная и результирующая башни имеют на вершинах самое маленькое кольцо.
Организовать бесконечный вывод данных о попе и его собаке.