3. Упрощенная процедура многофакторного эксперимента

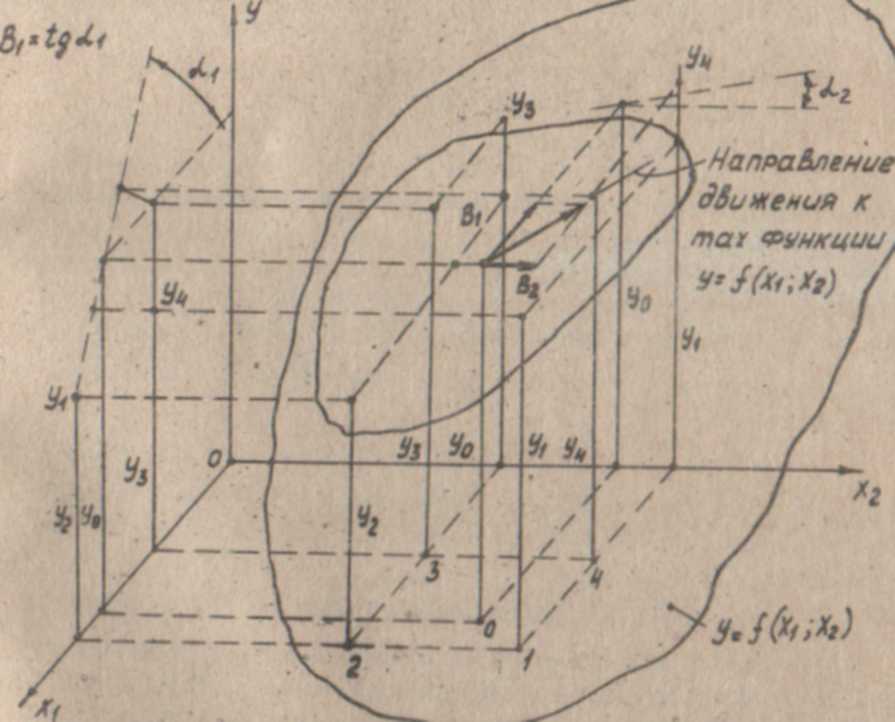
Обычно любой параметр ЭРЭ зависит от ряда факторов Х₁, X₂.. ...X,причем эта зависимость может быть представлена поверх­ностьюУ=(Х₁,Х₂....Х )что показано на рис3.1

рис 3.1

Целью проведения многофакторного эксперимента при исследо­вании ЭРЭ является получение математической модели зависимости заданного параметра от ряда факторов, а также прогнозирование положения экстремума. Модель получается в, виде полинома первого порядка (уравнение регрессии):

Y=b ₀ + (3.1)

где - значение функции в базовой точке, которая характеризуется параметрами X_io;

- коэффициента влияния, характеризующие чувствительность изучаемой зависимости и изменение соответствующего параметра X_i, отсчет кото­рого осуществляется от базовой точки.

Задачей эксперимента является нахождение коэффициентов b_o,b_i.

Таким образом, исследуемая поверхность y.=f(Xi) в выбран­ной ограниченной области значений факторов X представляется плоскостью, которая списывается выражением (3.1).

При исследовании полагаем, что точность измерений и изготовления, исследуемых образцов-высокая, случайные ошибки, связанные с невнимательностью экспериментатора - исключены, опыты заведомо воспроизводимы, все коэффициенты b_i заведомо значимы, адек­ватность модели впоследствии будет оценена приближенно. Поэтому статистическую обработку результатов измерений не проводим. С учетом высказанного можно принять следующий порядок эксперимента:

1) теоретическое изучение характера зависимости исследуе­мого параметра от факторов;

2) изучение методики измерений и измерительной аппаратуры;

3) определение возможных границ изменений факторов и выбор базовой точки, характеризуемой X_io , выбор шага варьирования параметров ∆Х_i;

4) составление матрицы планирования факторного эксперимента.

При этом осуществляется идея одновременного изменения всех факторов и рандомизация опытов (проведение их в случайной после­довательности) . Обычно факторы X_i изменяют на один шаг ±∆Хi. Увеличение X_i на ∆X_i в плане эксперимента обозначается как "+", уменьшение "-". Так как любой фактор принимает только два значения, то такой полный факторный эксперимент содержит 2ⁿ измерений, где n - число факторов. При трех факторах будет восемь измерений, при двух - четыре. Матрица планирования при трех факторах имеет следующий вид (матрица планирования для двух факторов обведена пунктиром):

№ опыта	Знак	Знак	Знак	У
1	-	-	-	У1
2	+	-	-	У2
3	-	+	-	УЗ
4	+	+	-	У4
5	-	-	+	У5
6	+	-	+	У6
7	-	+	-	У7
8	+	+	+	У8

5) измерение yi, причем с целью рандомизации опыты проводятся в произвольном порядке;

6) вычисление коэффициентов b_o, b_i и запись уравнения регрессии (построение математической модели), коэффициенты b_i определяются по формуле

.

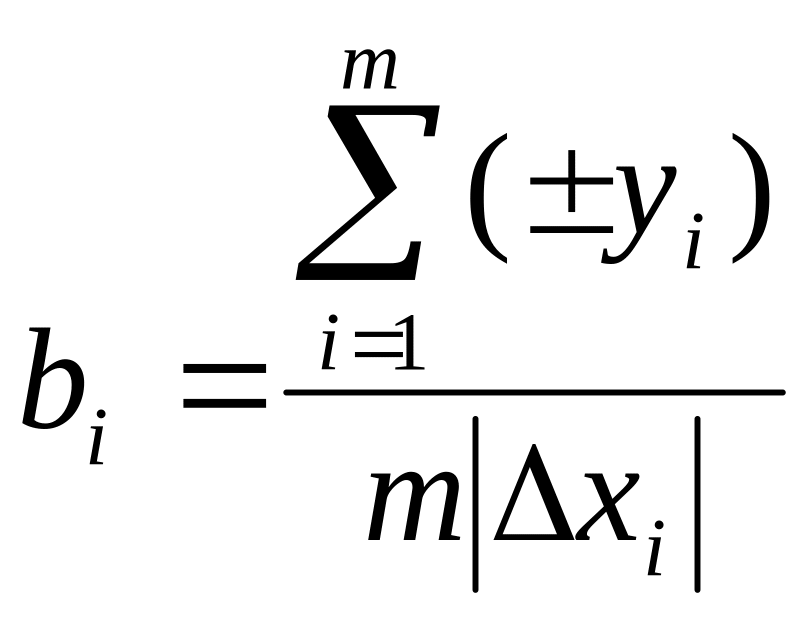где у_i - значение Y при опытах со знаками, соответствующими знакам ∆Х_i (берутся из столбцов матрицы планиро­вания);

m - число опытов (строк матрицы планирования).

Коэффициент b_o также находится по вышеприведенной фор­муле, но все y_i берутся со знаком "+ ", ∆Х_i опускаются. Для упрощенной проверки адекватности модели необходимо замерить у_о в базовой точке и сравнить со значением b_о . Если y_o= b_o , модель адекватна, если y_o≠ b_o, модель неадекватна с "Неувязкой" , причем если < 10%, то можно приближенно считать модель адекватной;

7) определение направления движения к экстремуму функции.

При уже известном уравнении регрессии, вычисляя значения У при увеличенном X_i, равном (2 + 4)∆Х_i, можно составить представление о направлении увеличения функции У. При двух фак­торах направление движения к экстремуму функции совпадает с направлением вектора N, являющегося геометрической суммой векторов b₁ и b₂ (см.рис.3.1).

Прогнозируемое значение У должно сверяться с эксперименталь­ным его значением. При большом расхождении теории с эксперимен­том (например, более 10%) необходимо выбрать новое положение базовой точки и повторить пункты 3 - 7 до попадания в экстремум функции.

При попадании базовой точки в экстремум ,т.е.

Предлагаемая процедура проведения эксперимента является упрощенной. Вводя нормирование коэффициентов, проводя опыты с учетом статистики, оценивая значимость коэффициентов по критерию Стьюдента, воспроизводимость опытов - по критерию Кохрана и адекватности модели по критерию Фишера, можно более качественно спланировать эксперимент.