7 Короткі теоретичні відомості та методичні вказівки, що необхідні для виконання лабораторних робіт

Лабораторна робота №1

Побудова математичних моделей економічних задач

Хід роботи.

1. Уважно прочитати умови задач. Виділити дані параметри та невідомі, виявити зв’язки між ними. Проаналізувати питання задач.

2. Визначити вектор керованих параметрів х, включаючи одиниці виміру.

3. Побудувати систему обмежень задачі, які відображають зв’язок відомих (екзогенних) та невідомих (ендогенних) параметрів. Вказати їх економічний зміст.

4. Перевірити правильність системи обмежень. Для цього порівняти одиниці виміру правих та лівих частин обмежень.

5. Побудувати цільову функцію задачі – функцію, яка формалізує поняття цілі, потреб системи. Вказати її економічний зміст.

6. Охарактеризувати отриману модель. Визначити до якого класу вона належить:

• детермінована або стохастична;

• динамічна або статична;

• дискретна або неперервна.

Задача

Нехай контора матеріально-технічного постачання реалізує три види продукції: П1, П2, П3. Для цього використовуються два обмежених ресурси - корисна площа приміщення, що з урахуванням коефіцієнта оборотності становить 460 кв. м і робочий час у 500 люд/год. Товарообіг підприємства повинен бути не менше 240 тис. грн. Необхідно розробити план товарообігу, що дає максимум прибутку. Вихідні дані наведені в таблиці.

Ресурси	Затрати ресупсів на одиницю продукції			Об’єм ресурсів
	П1	П2	П3
Корисна площіна, кв.м	1,5	2	3	460
Робочий часб люд./год.	3	2	1,5	500
Прибуток, грн.	50	65	70	max z
План	x1	x2	x3

Скласти математичну модель задачі й привести її до канонічного виду.

Позначимо через x1, x2 й x3 об’єми продукції, що підлягає реалізації. Модель задачі матиме вигляд мах: F(x) = 50x1+65x2+70x3

1,5x1+2x2+3x3 , 460

3x1+2x2+1,5x3 500

xj 0, j =1, 3

Лабораторна робота №2 Графічний метод розв’язування задачі лінійного програмування Хід роботи.

Нехай задана задача лінійного програмування з двома змінними:

Z= c₁ x₁ +c₂ x₂ max ( min ), (2.1)

a_i1 x₁+a_i2 x₂₂ R b_i, i=1,m, R{  , , } (2.2)

1. Побудувати множину припустимих рішень з урахуванням системи обмежень (2.2).

2. Побудувати вектор градієнтного напрямку.

3. Провести довільну лінію рівня цілі Z = const, перпендикулярно до вектору С.

4. При вирішенні задачі на max переміщуємо пряму Z = const у напрямку вектора С так, щоб вона зайняла крайнє положення. При подальшому її переміщенні лінія рівня цілі не мають спільних точок з множиною припустимих рішень . У випадку розв’язання задачі на min лінії рівня цілі Z = const переміщуємо в антіградієнтному напрямку.

5. Визначаємо оптимальний план. Можливі наступні випадки:

а) Оптимальний план єдиний. Тоді лінія рівня цілі і множина у крайньому положенні будуть мати одну спільну точку.

б) Оптимальних планів може бути нескінченна множина. У цьому випадку в крайньому положенні лінія рівня цілі проходить через грань множини.

в) Цільова функція не обмежена, оскільки лінія рівня цілі, скільки б ми її не переміщували, не займає крайнього положення з множиною припустимих рішень.

г) Задача рішень не має, так як множина припустимих рішень пуста множина, тобто система обмежень несумісна.

Задача

Майстерня виготовляє два види продукції, використовуючи два ресурси: першого виду – 156 одиниць, другого – 63. Прибуток від реалізації одиниці першого виду продукції – 4 грн., другого – 6 грн. Норми витрат представлені у таблиці.

Ресурси	Витрати на од-цю продукції		Об’єм ресурсу
	П-1	П-2
1 2	2 0.5	1.6 0.8	156 63
Прибуток, грн.	4	5	Max Z
План	X1	X2

Визначити план-випуск, який максимізує прибуток. Побудуємо модель задачі. Нехай X = (X1,X2) - шуканий план випуску. Тоді модель набуває вигляду:

max:Z = 4X₁+5X₂ при обмеженнях:

Побудуємо багатокутник рішень. Для цього на площині в системі координат X₁ОХ₂ зобразимо граничні прямі:

2X₁+1,6Х₂ = 156;

0,5X₁+0,8X₂ = 63.

Візьмемо будь-яку точку площини, наприклад, початок координат та з‘ясуємо, яку напівплощину визначає відповідна нерівність. Напівплощину, яку визначає відповідна нерівність, зображено на малюнку штрихами. Враховуючи умову невід’ємності, багатокутник рішень задачі зобразимо чотирикутником ОАВС.

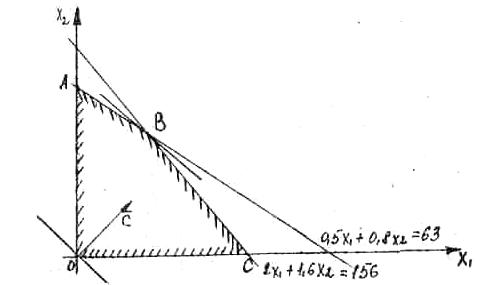
Далі, побудуємо будь-яку лінію рівня цілі, наприклад, Z=0. Для цього зобразимо вектор градієнтного напрямку С = (4;6). Оскільки вектор є необхідним лише для визначення напрямку найскорішого зростання цільової функції, то, враховуючи масштаб малюнку, можна для більшої наочності збудувати вектор С ( > 0), у нашому випадку вектор 10С. Через початок координат проведемо пряму, перпендикулярну до вектора С. Пряму Z = 0 зміщуємо паралельно до самої себе в напрямку вектору С в крайнє положення (точка В). У цій точці функція цілі дістає найбільшого значення. Вирішуючи сумісно рівняння прямих АD і ВС, знаходимо координати точки В X₁=30, Х₂=60, max Z = 420. Таким чином, майстерня повинна виготовляти 30 одиниць продукції першого виду і 60 – другого. Максимальний прибуток складає 420 грн.

Зауваження.

Графічно можна також вирішувати задачу лінійного програмування з n>2 змінними, якщо в її канонічному запису кількість невідомих n та кількість лінійно незалежних рівнянь m зв‘язані співвідношенням n-m=<2 (тобто ранг системи обмежений).