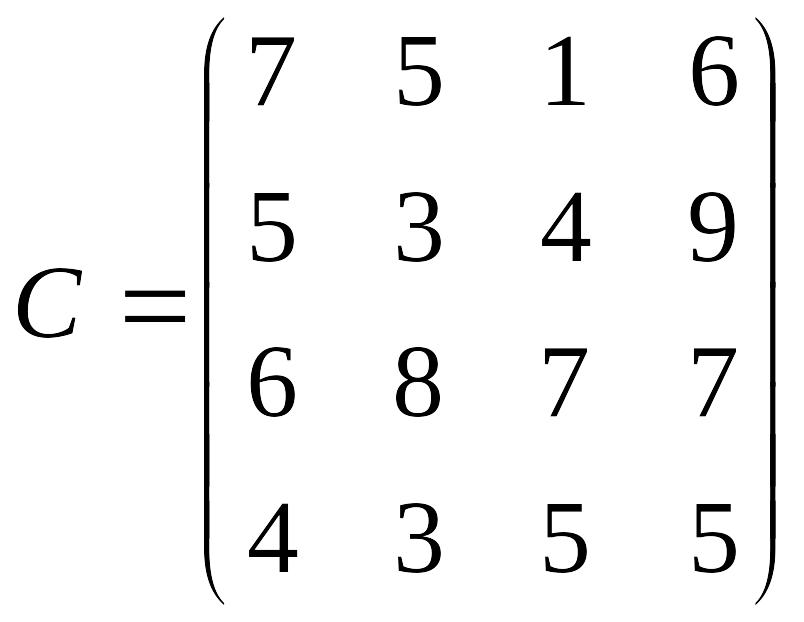
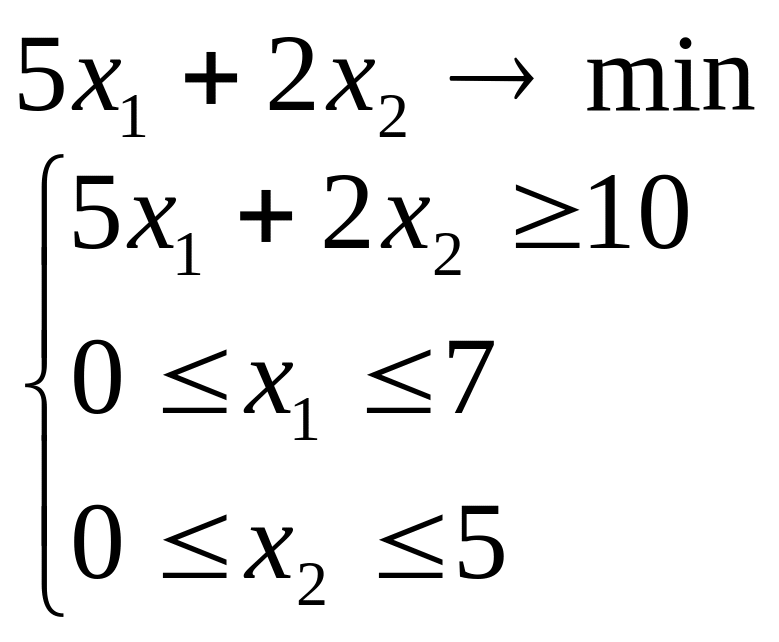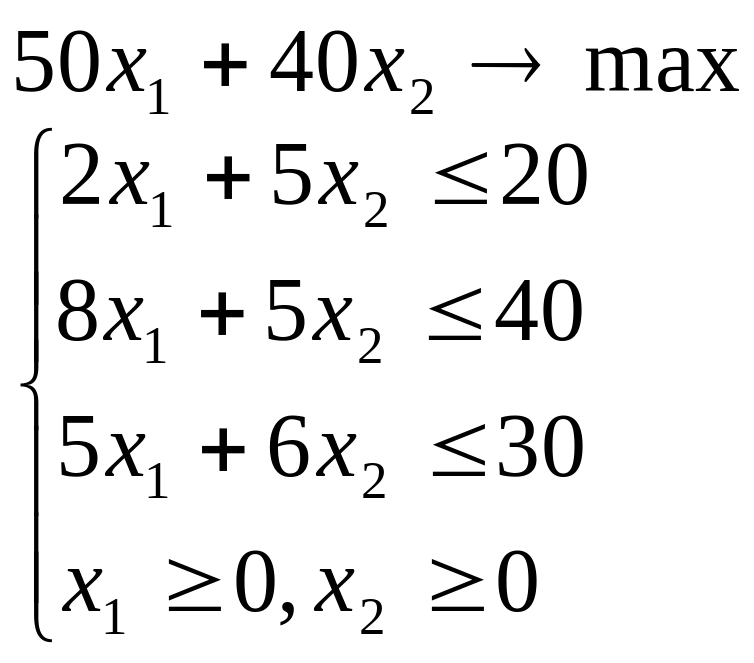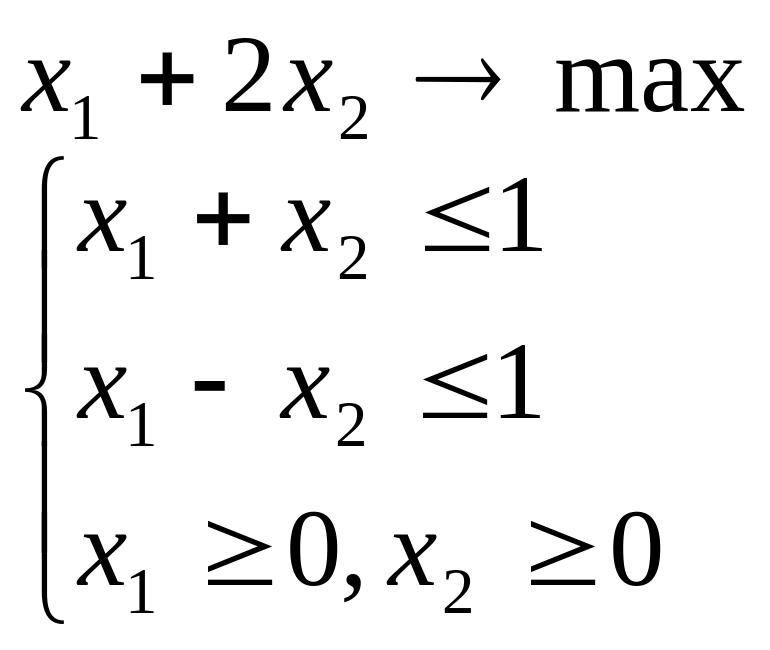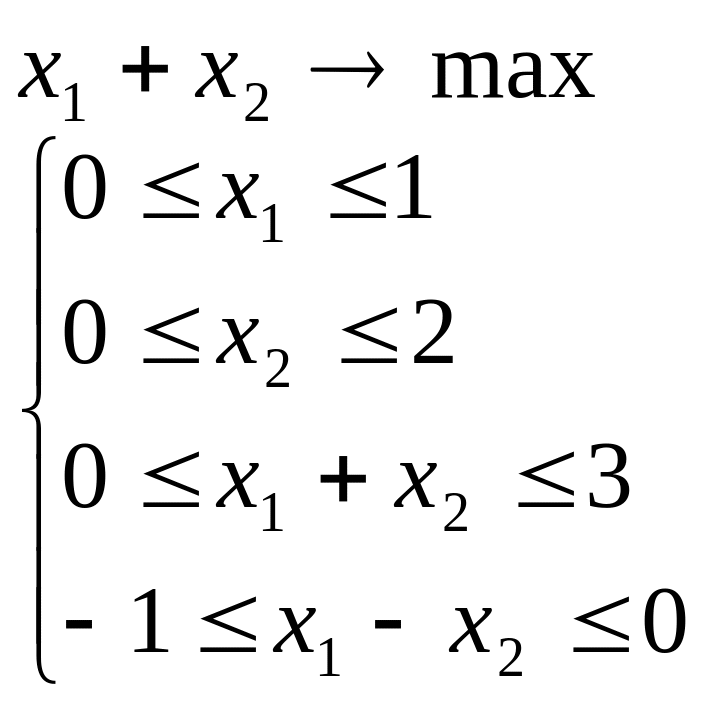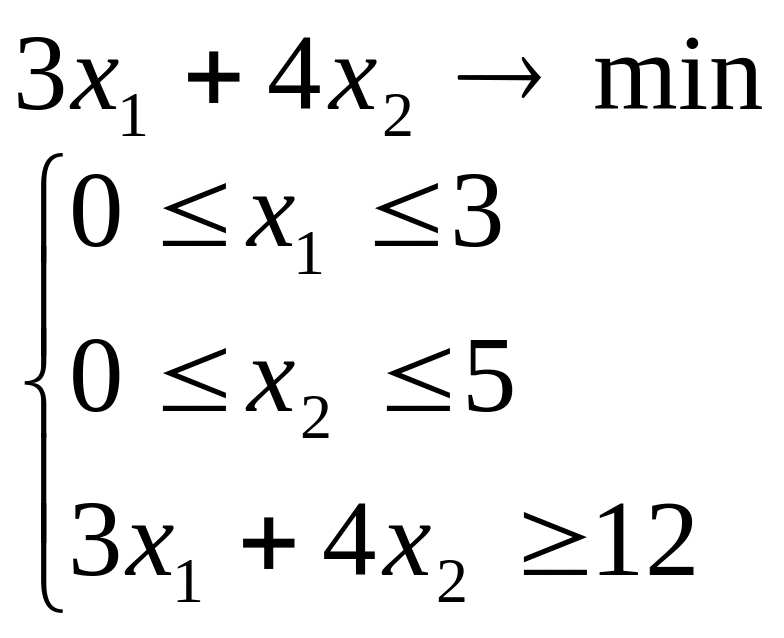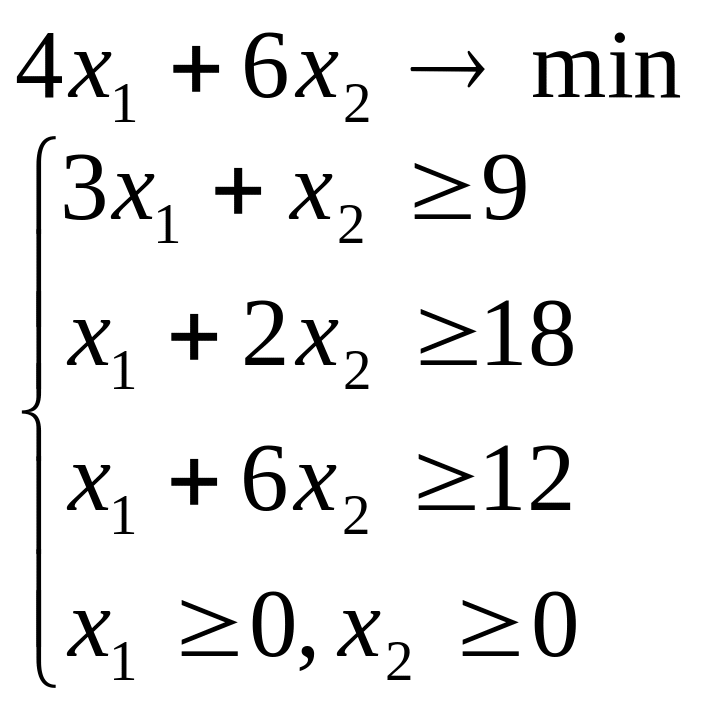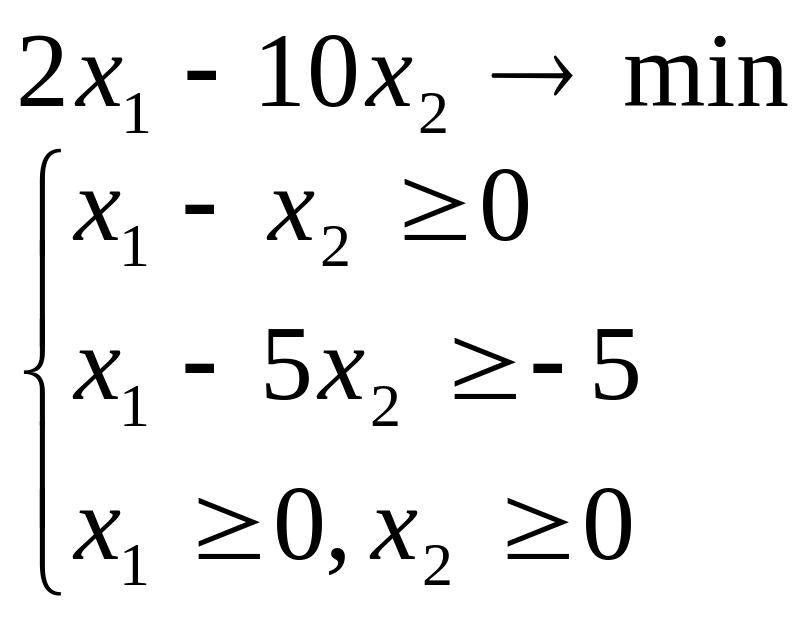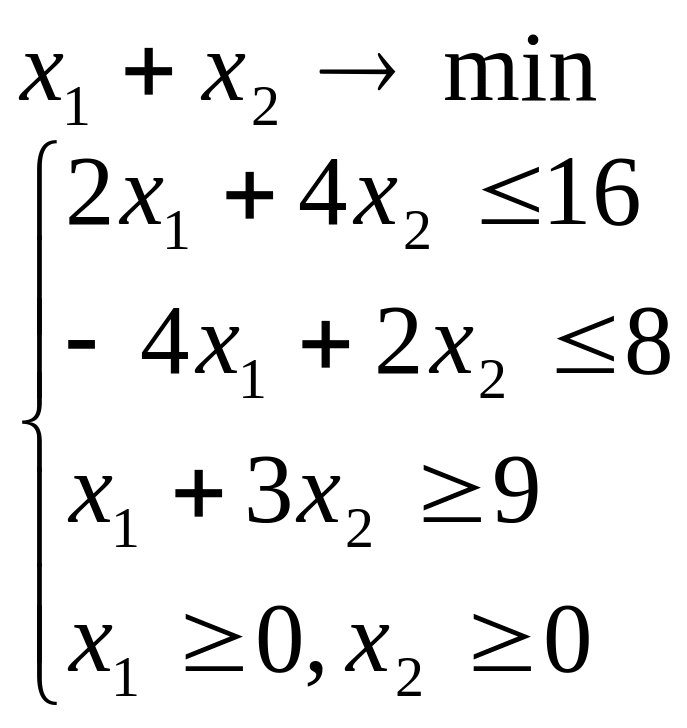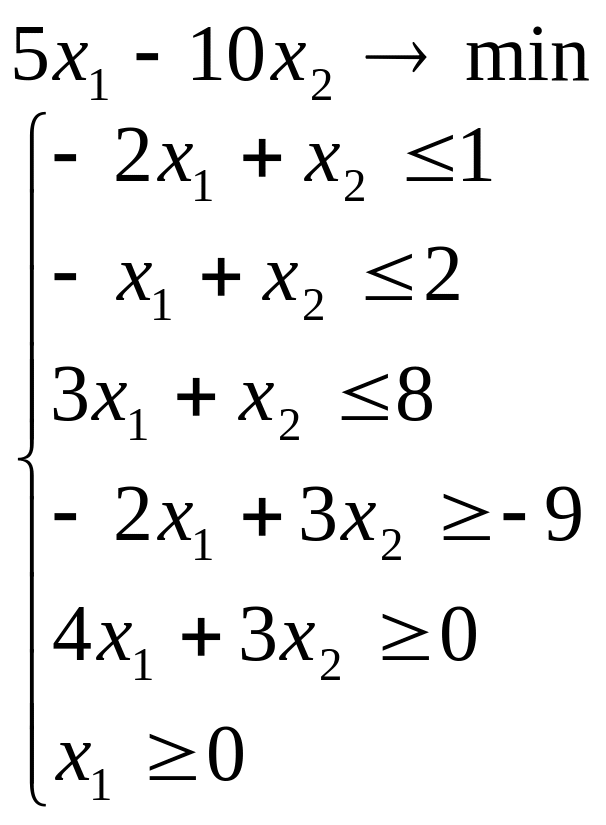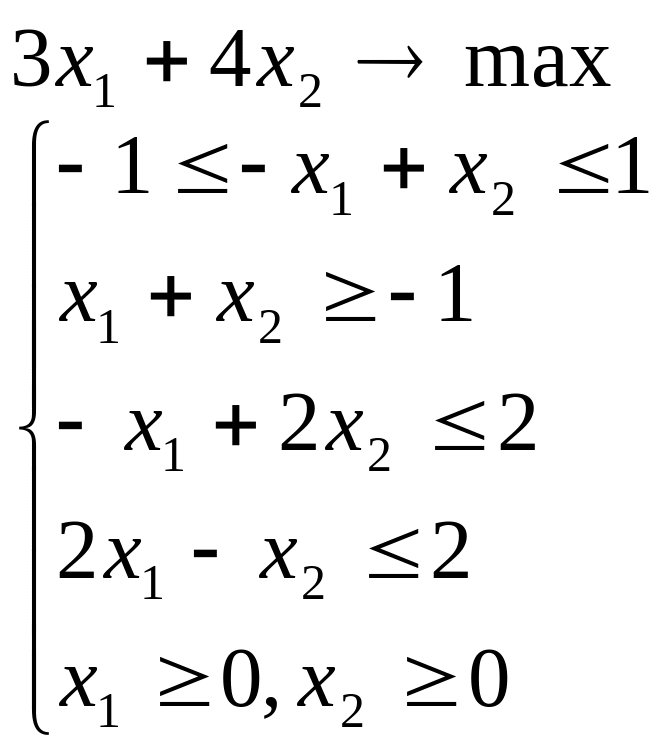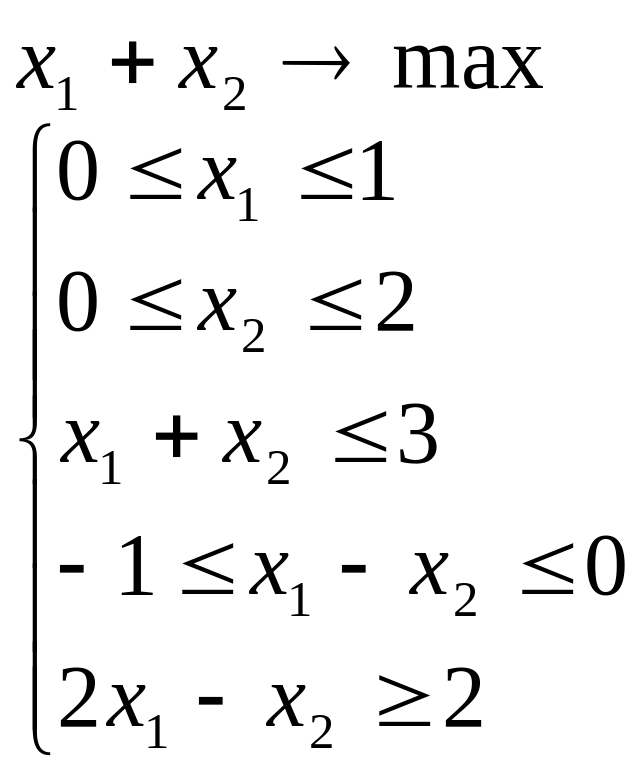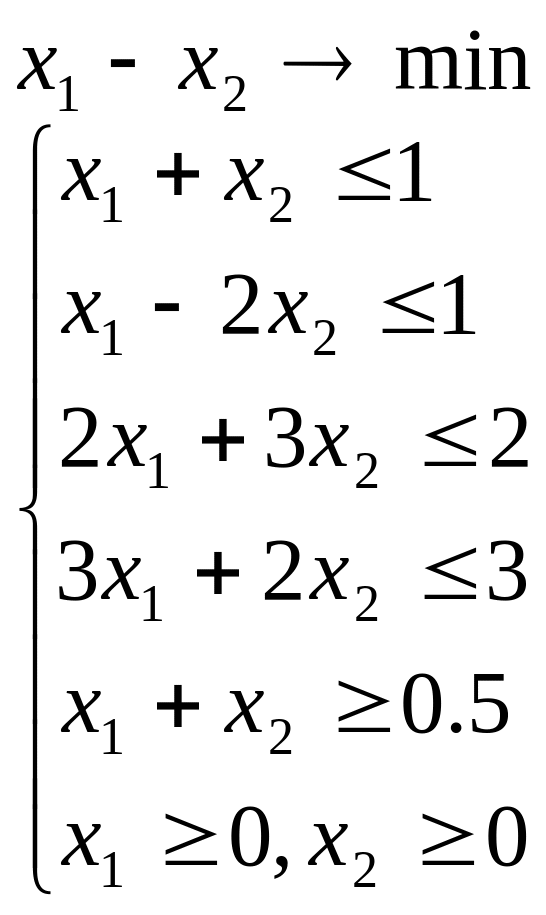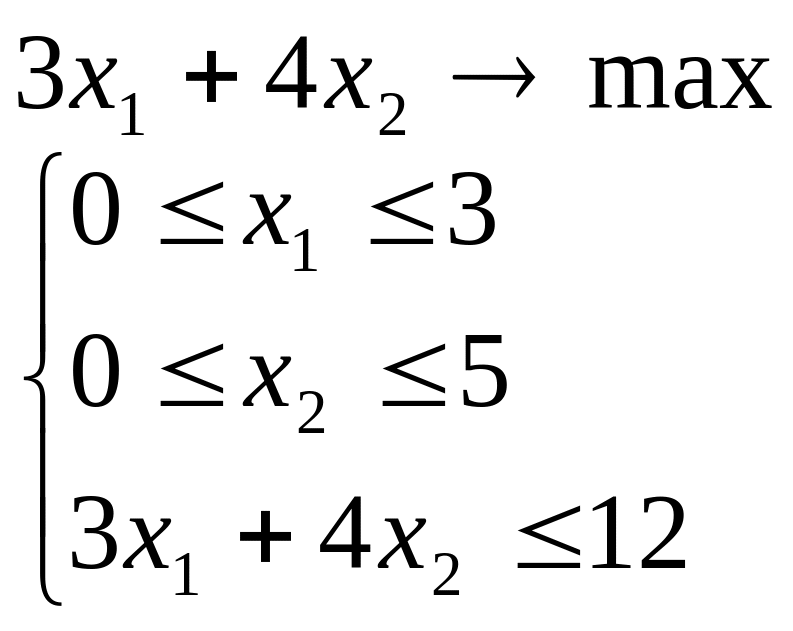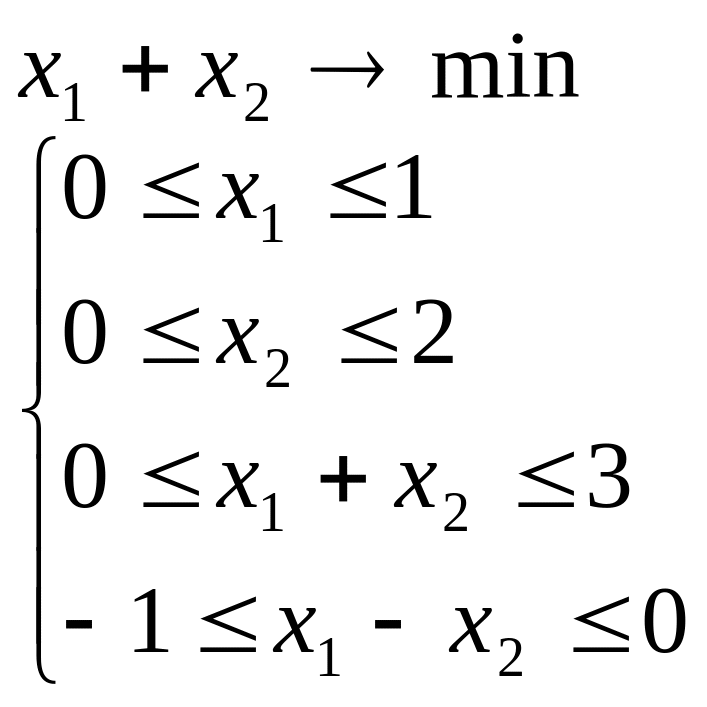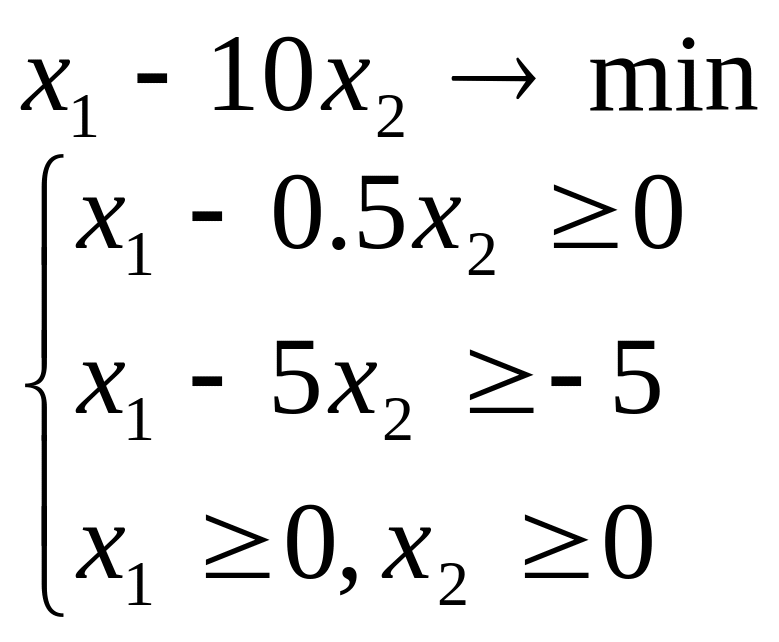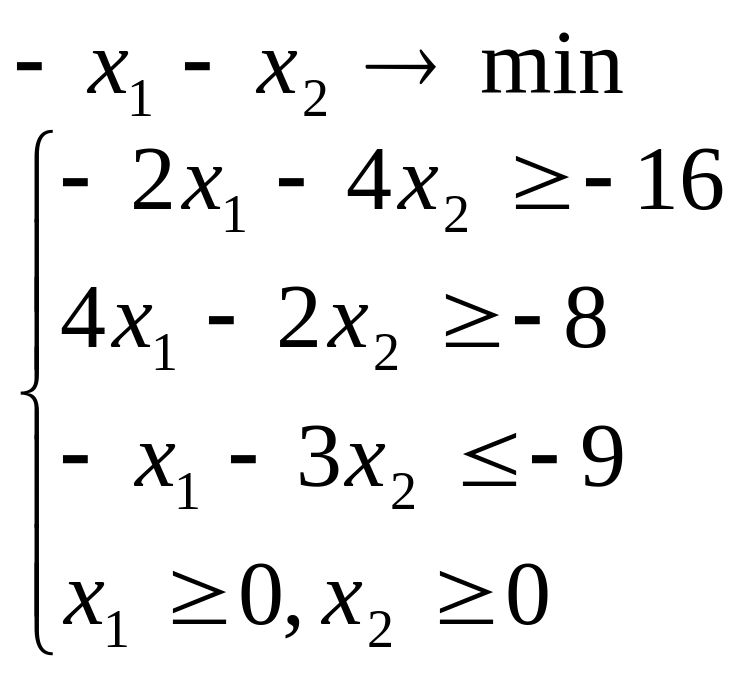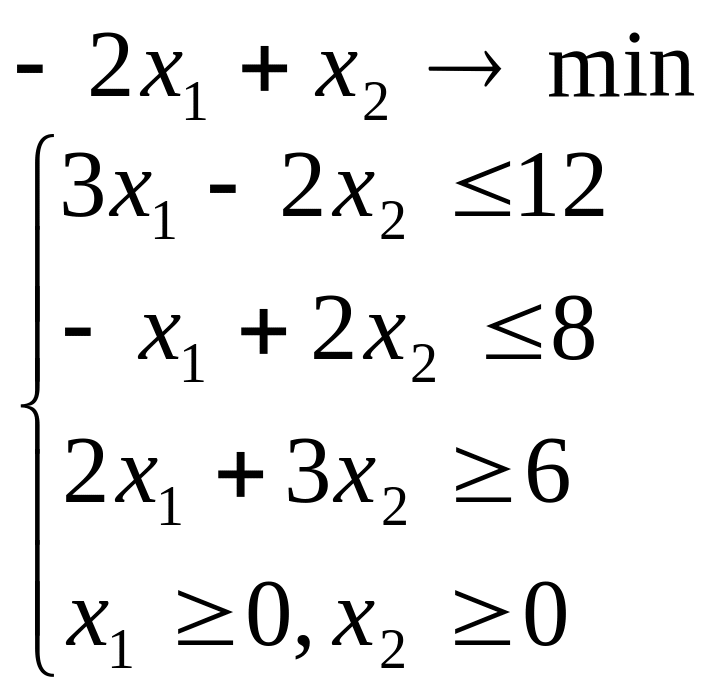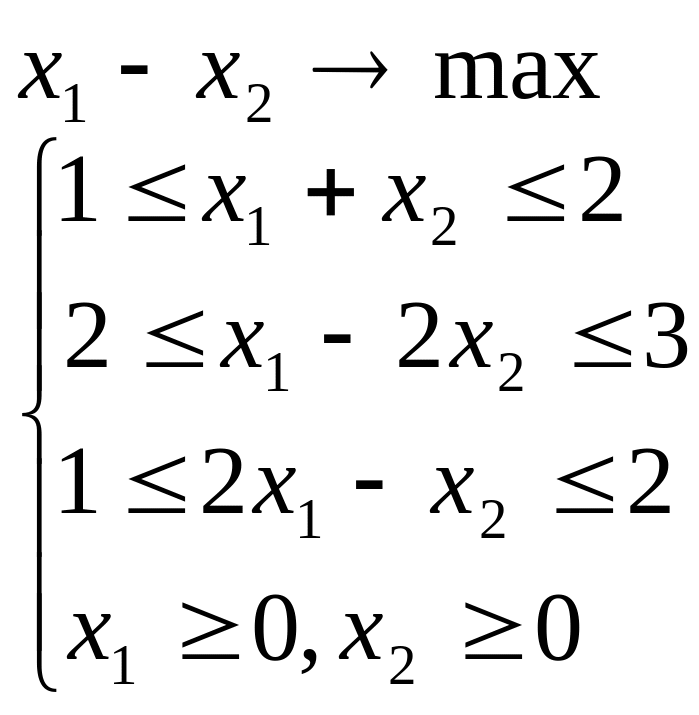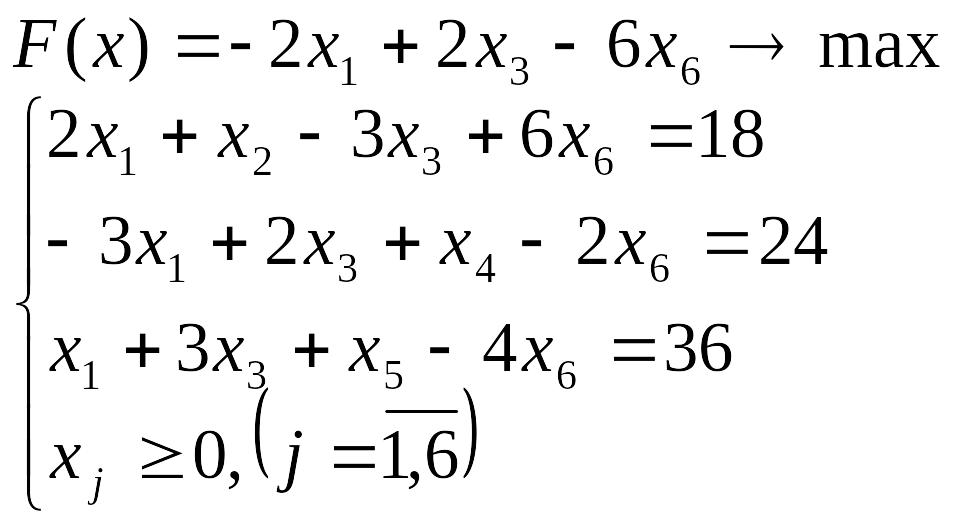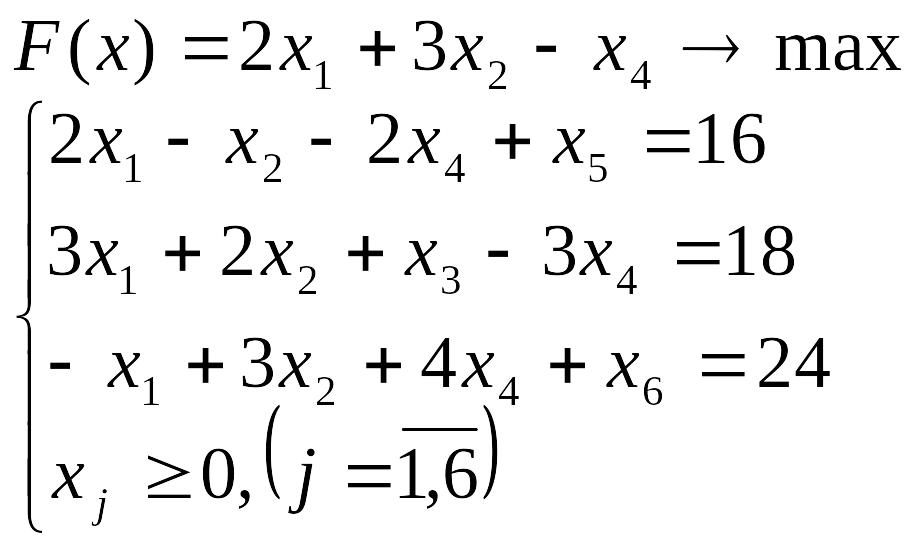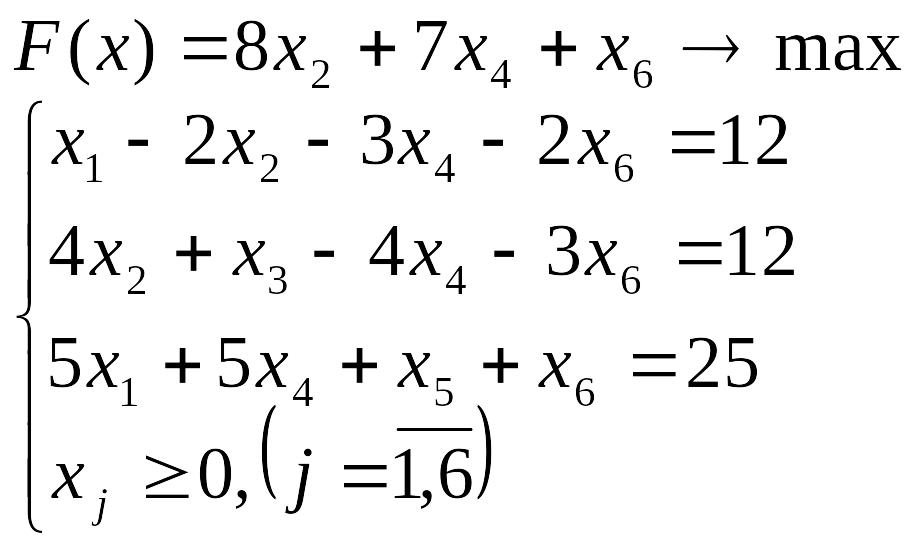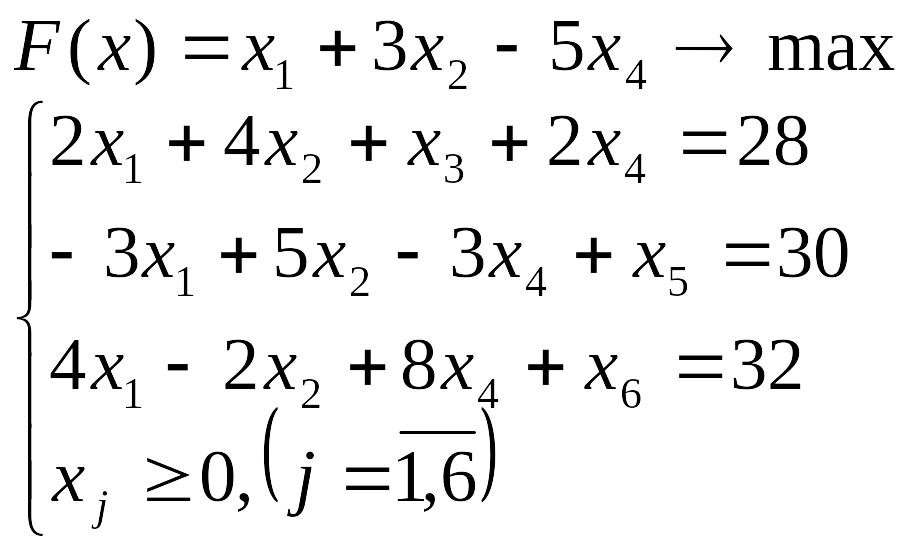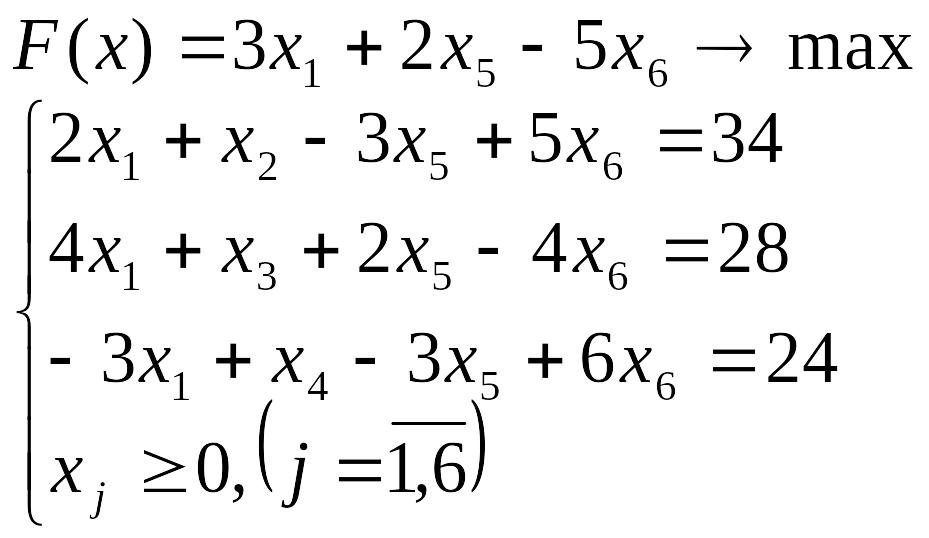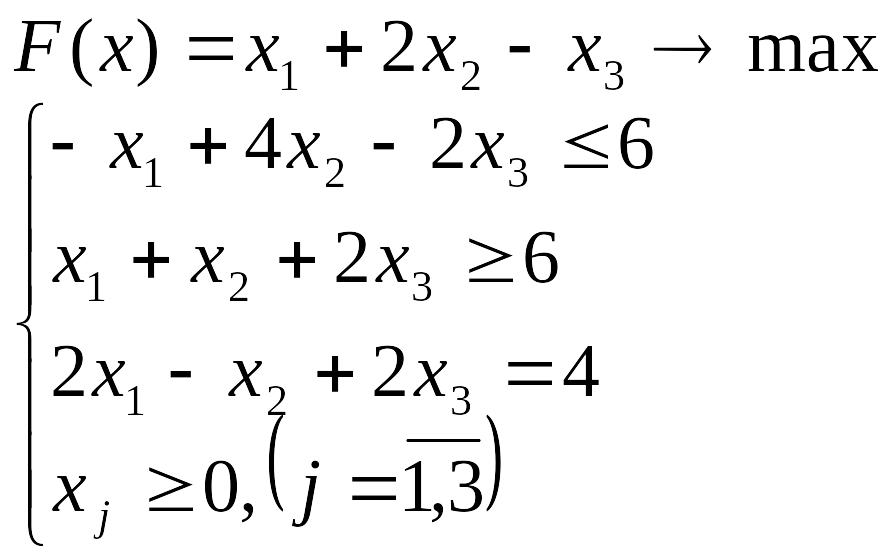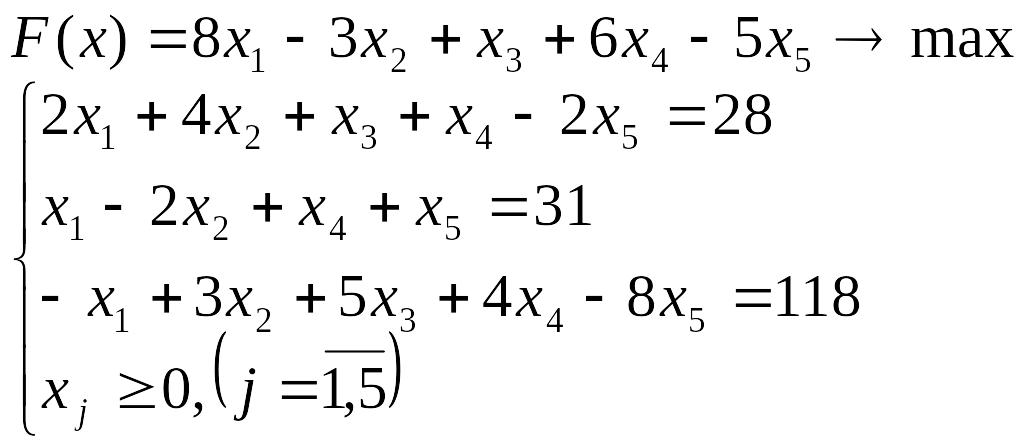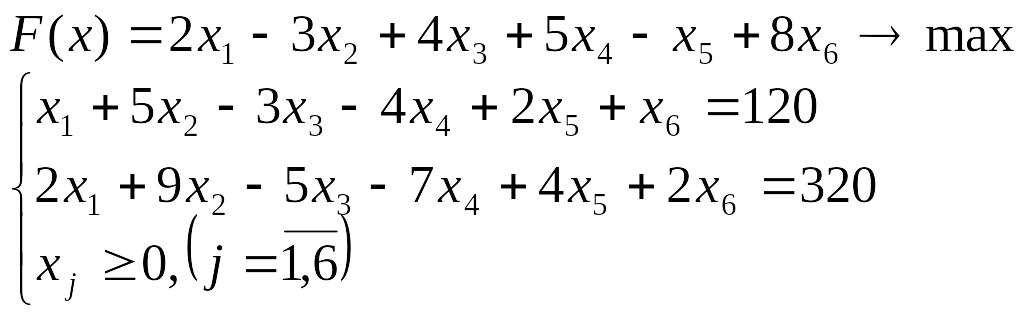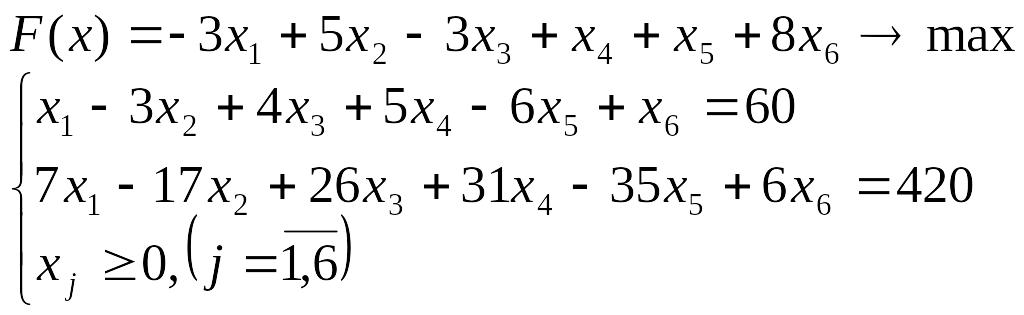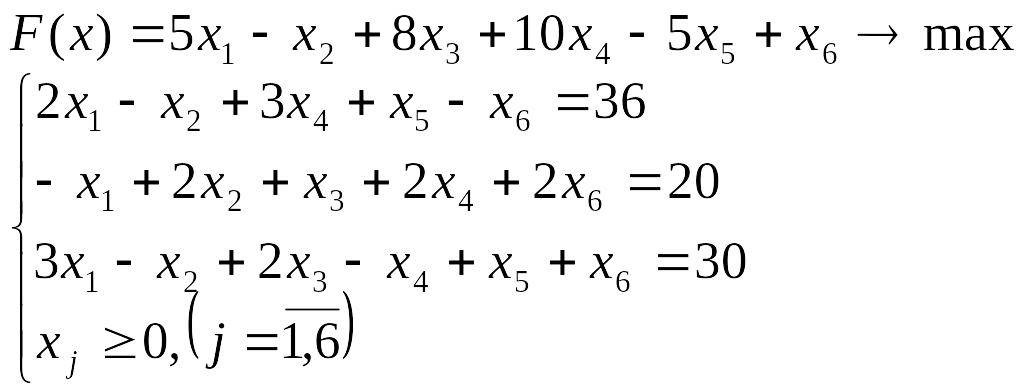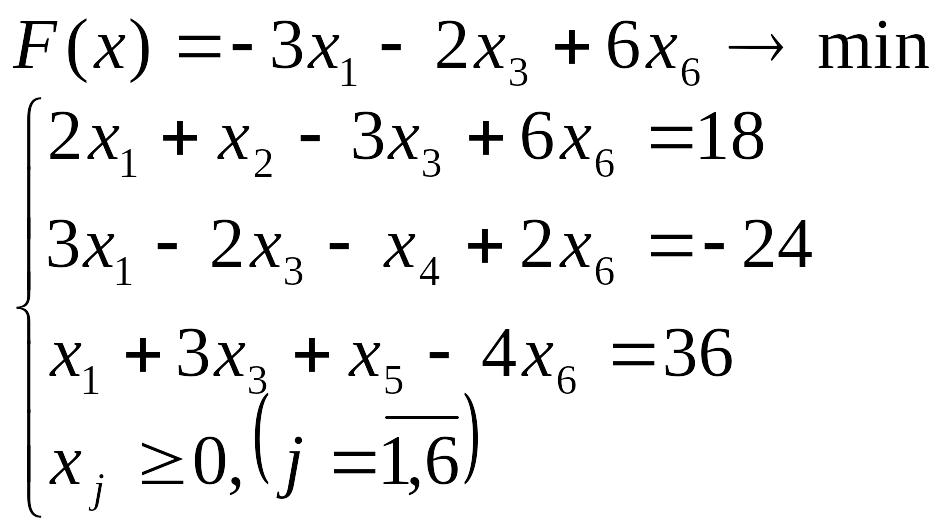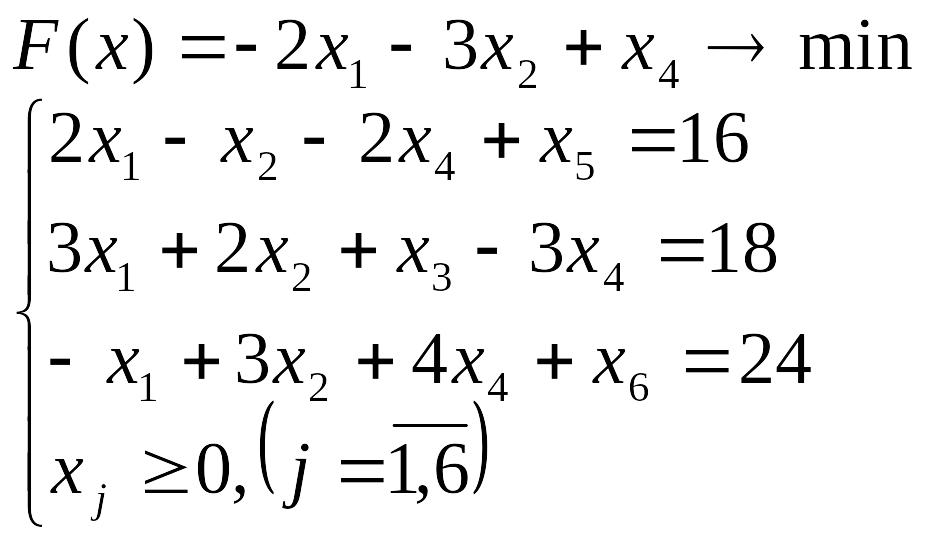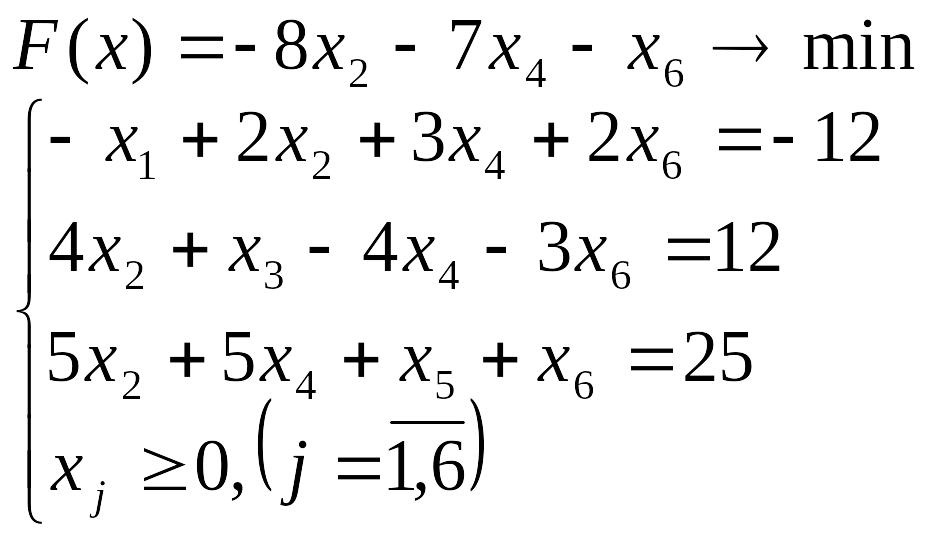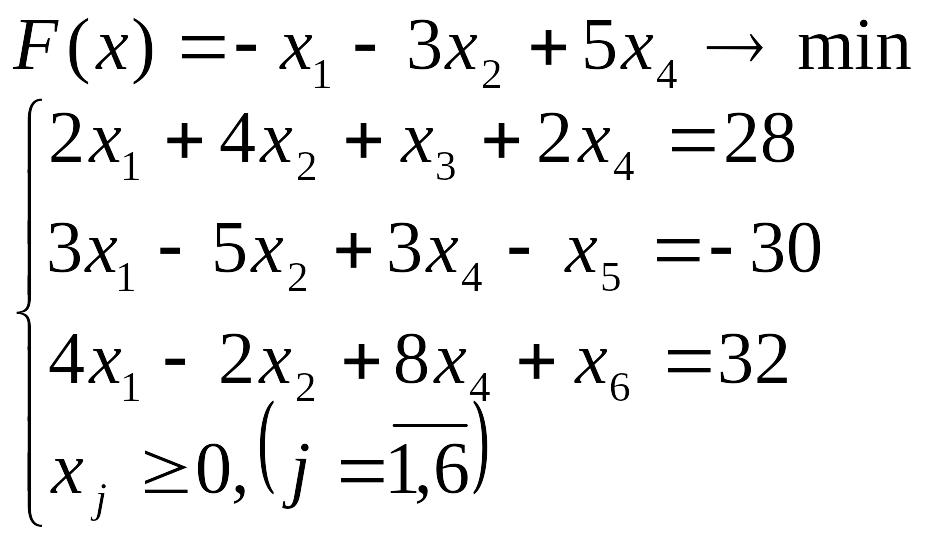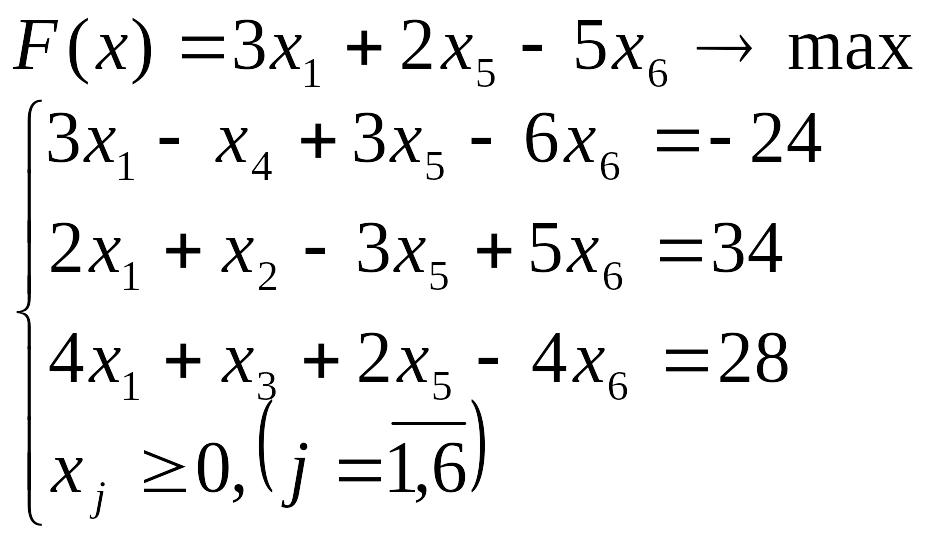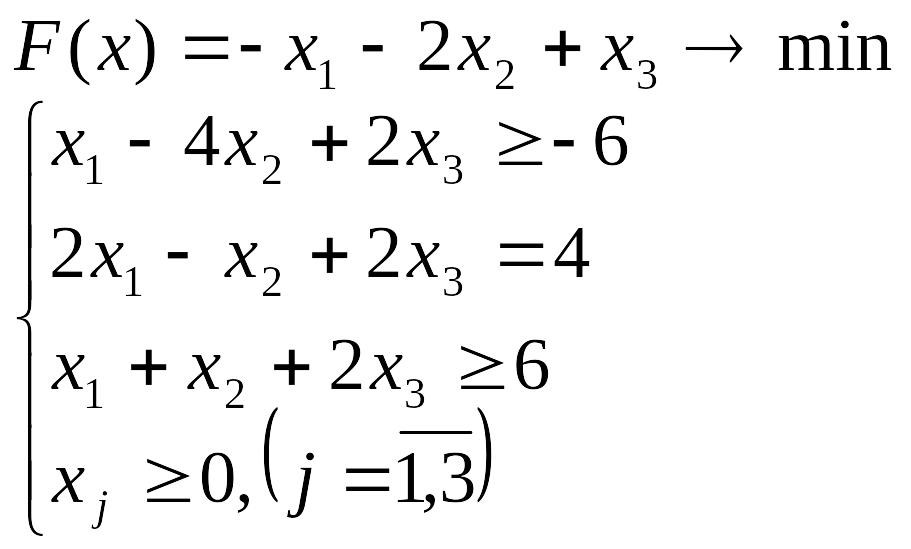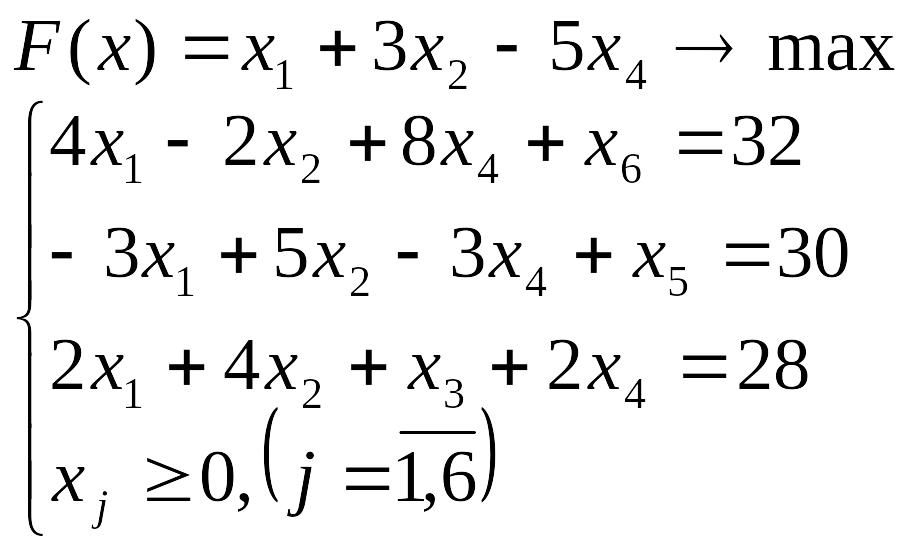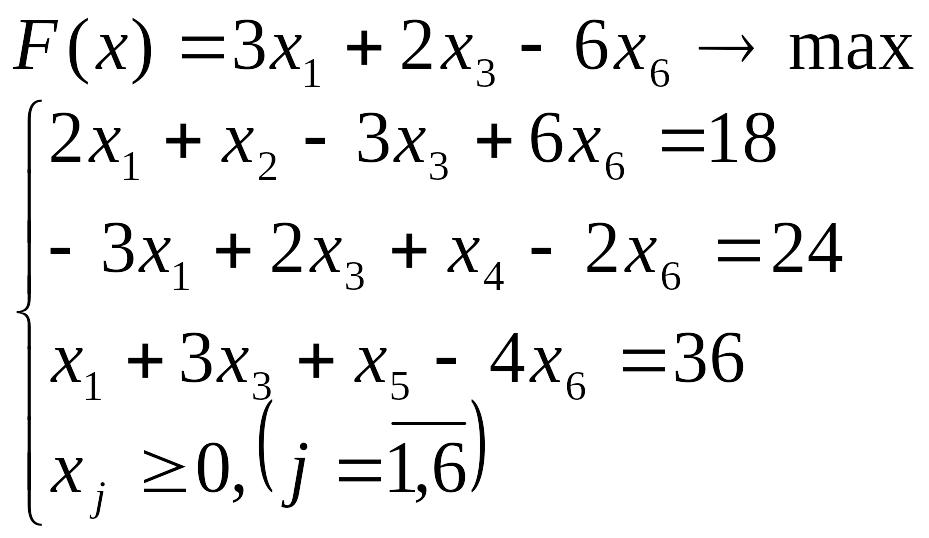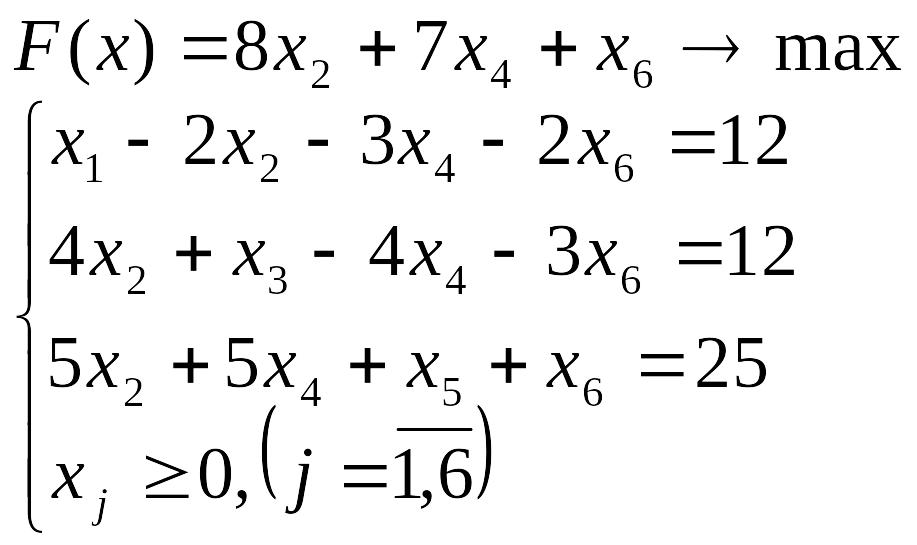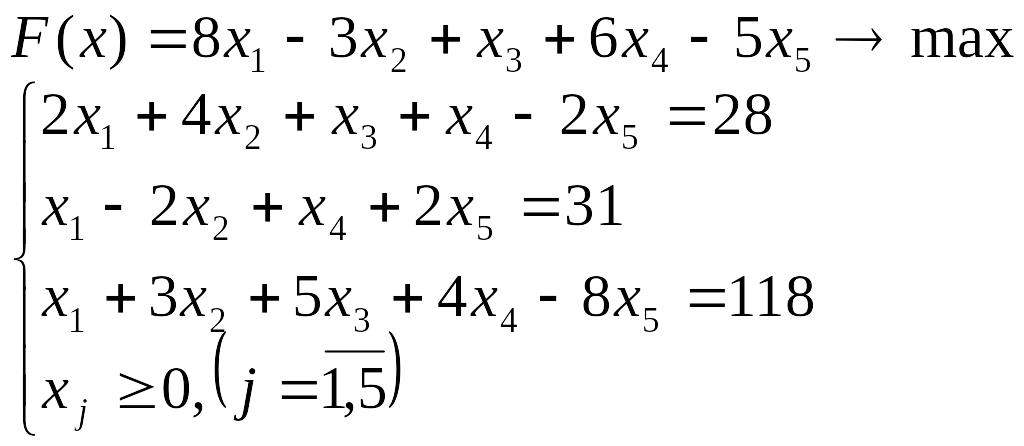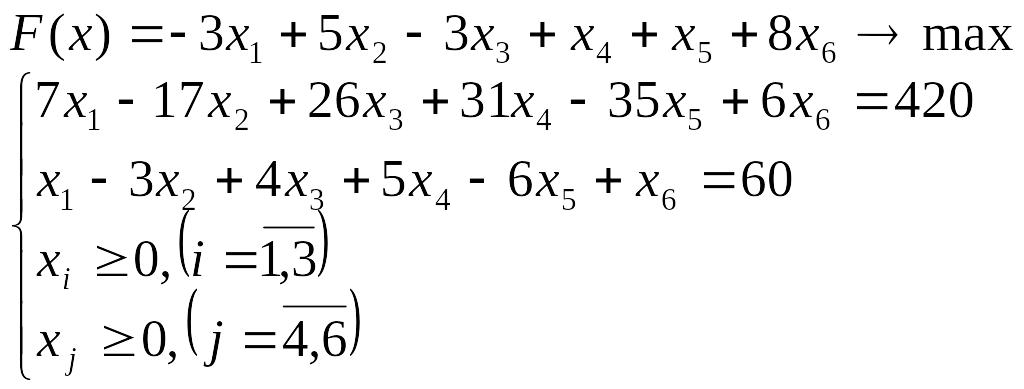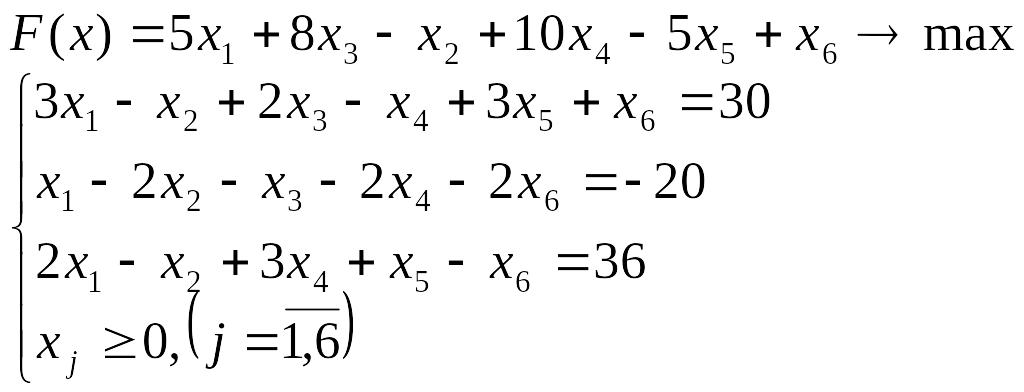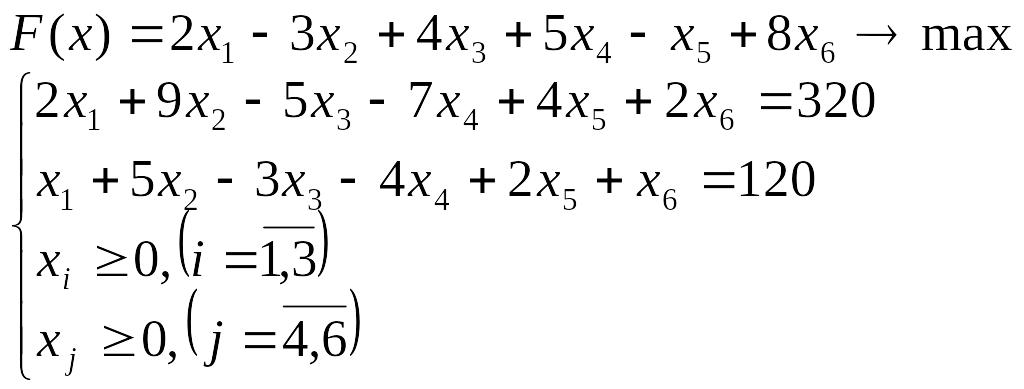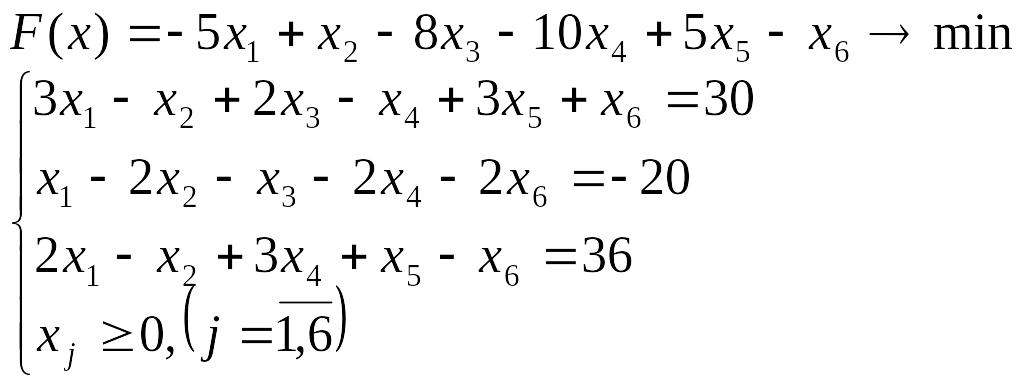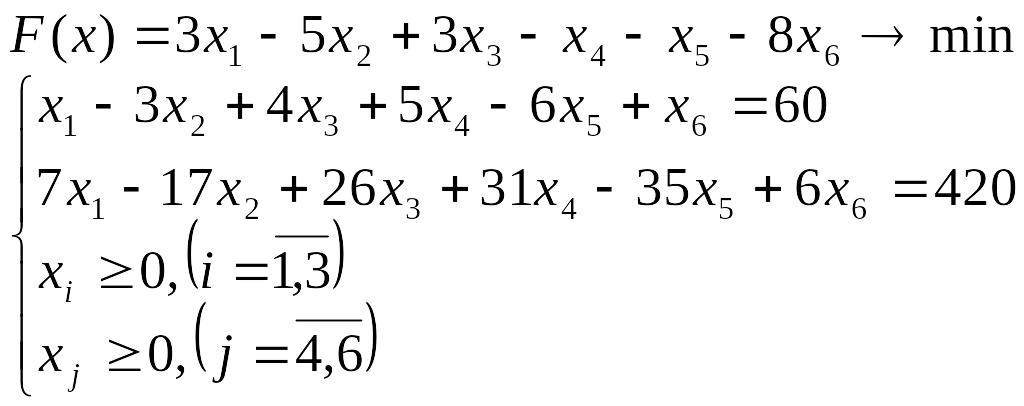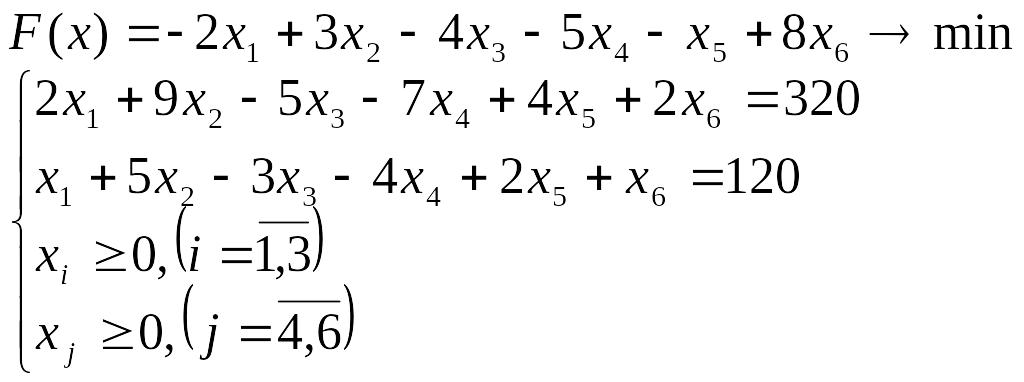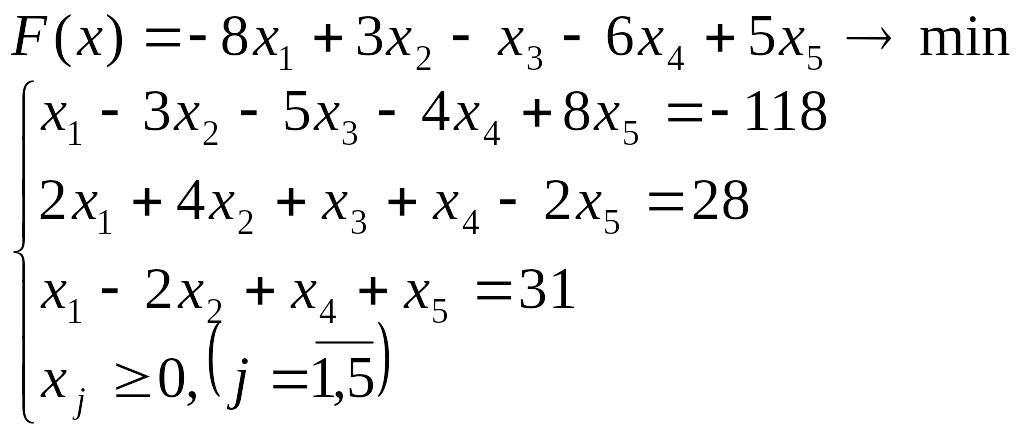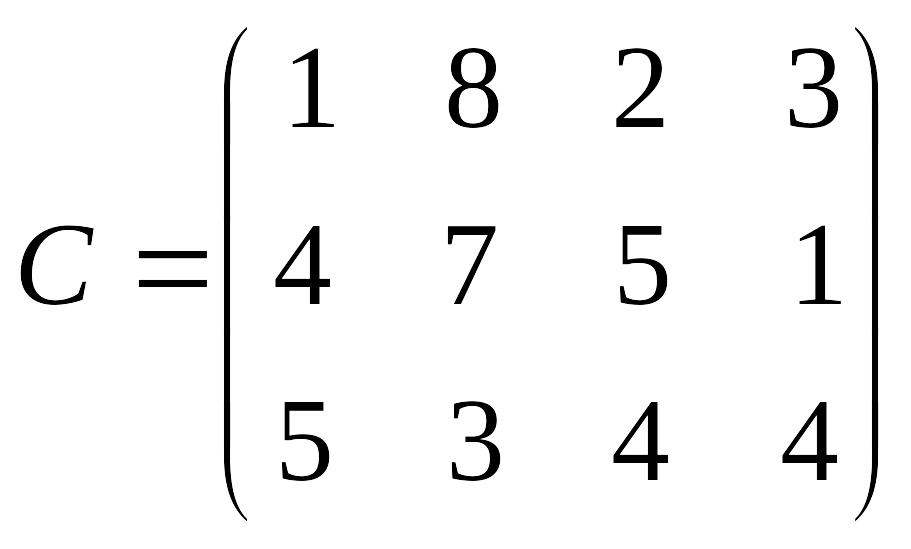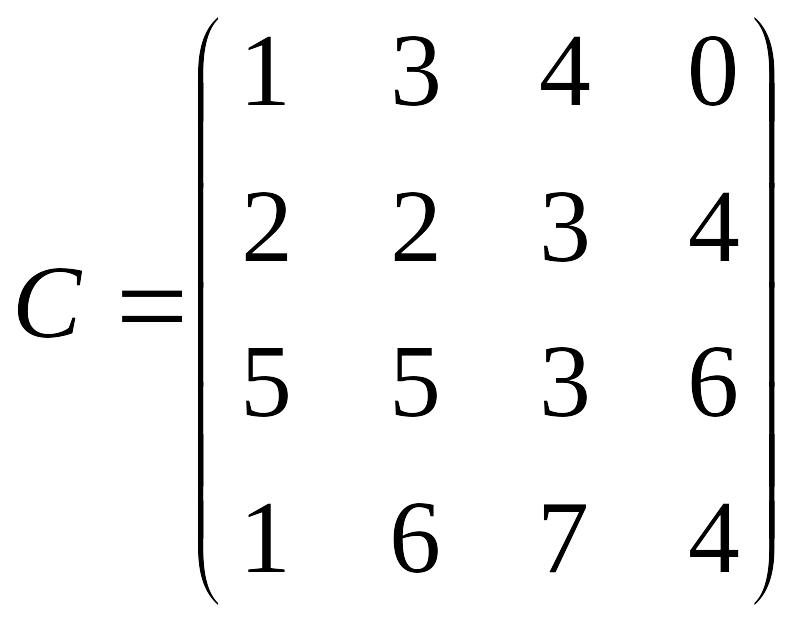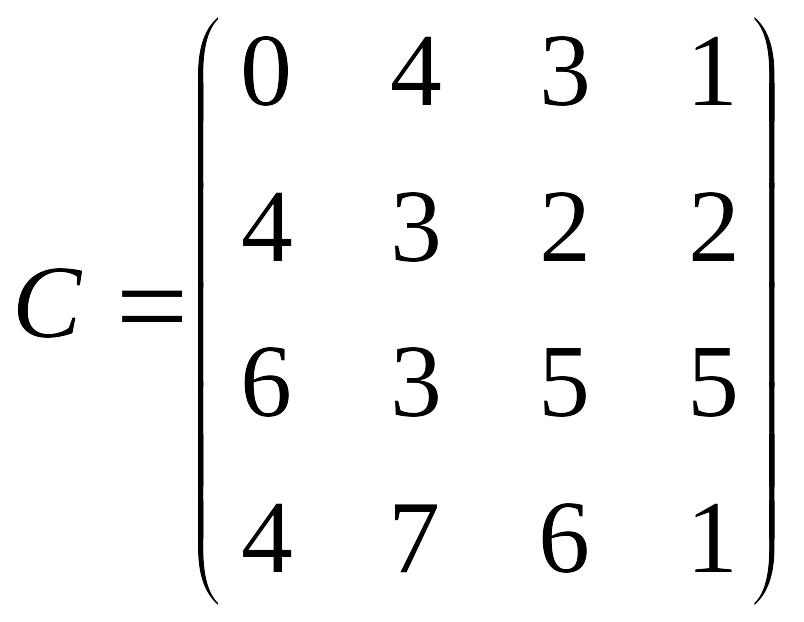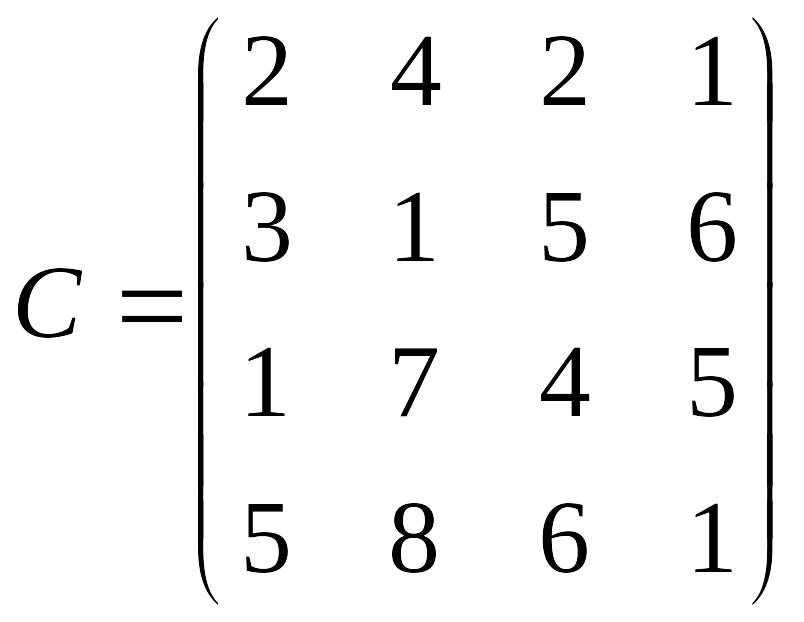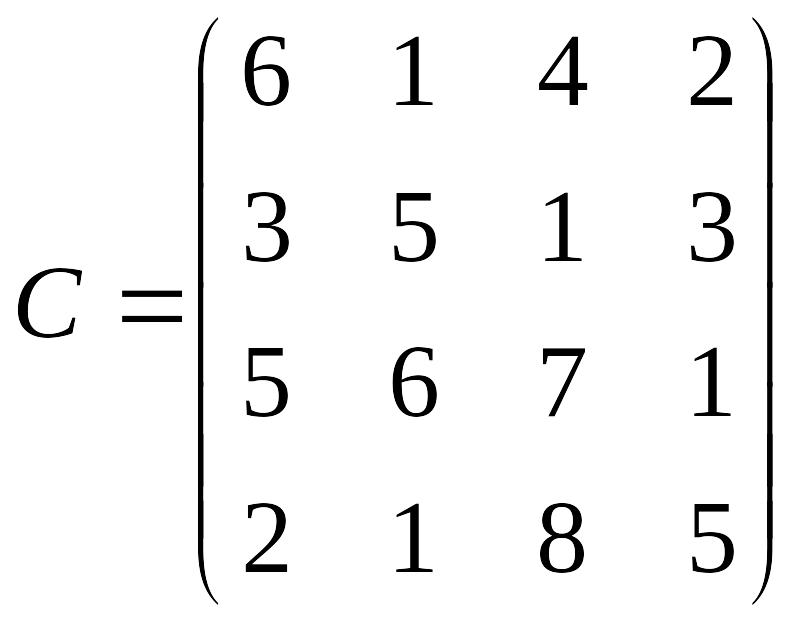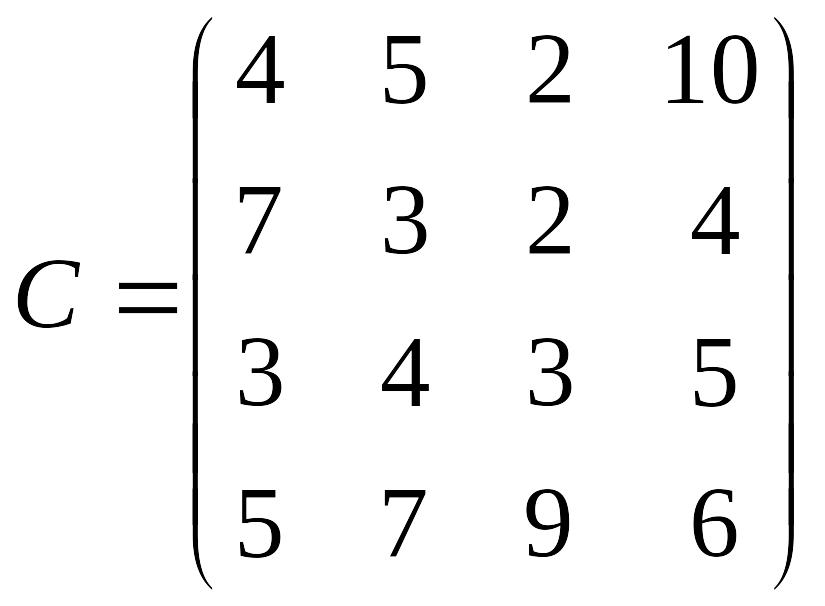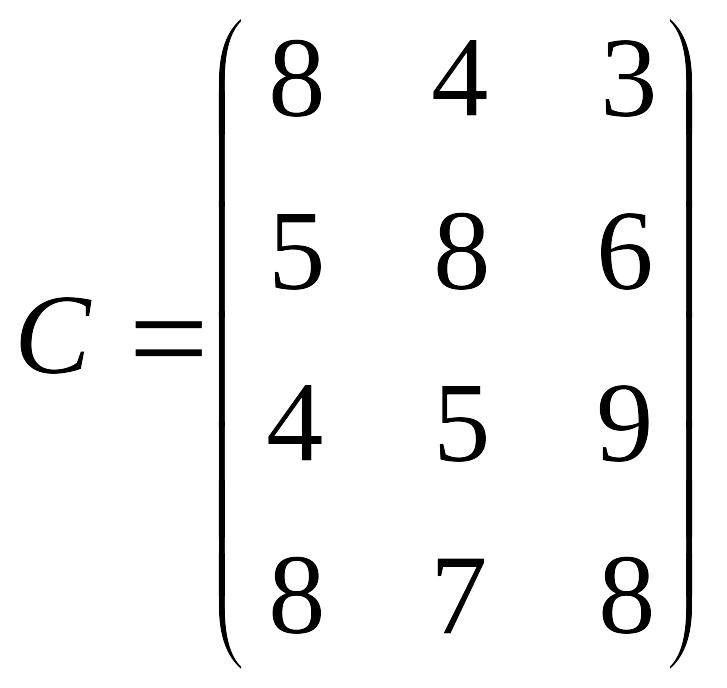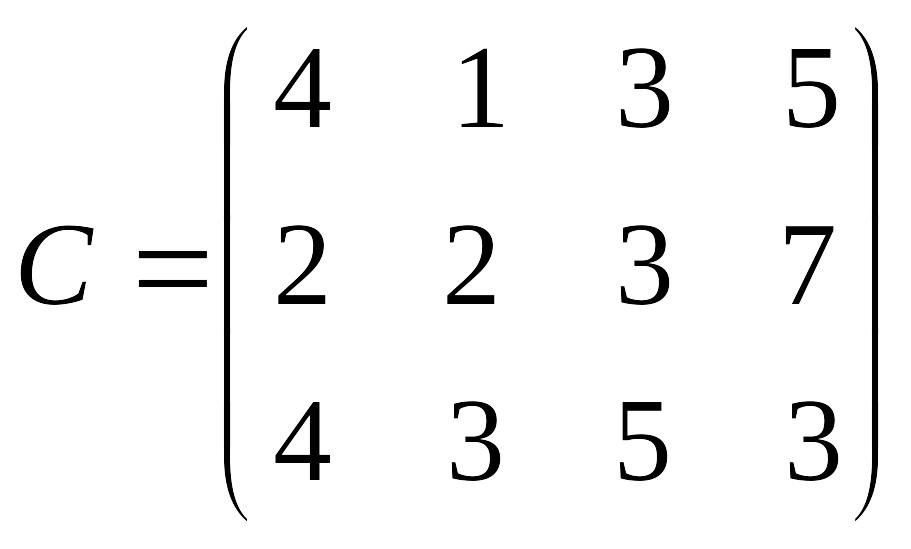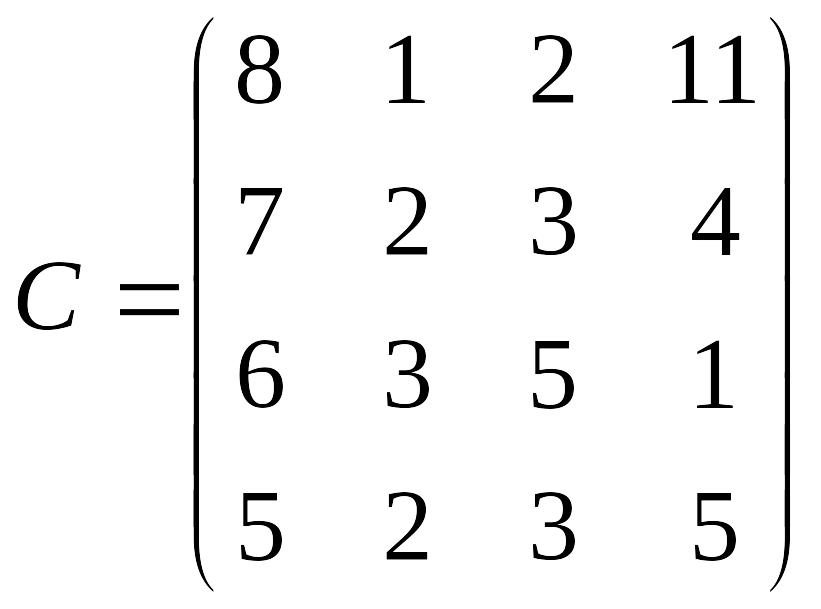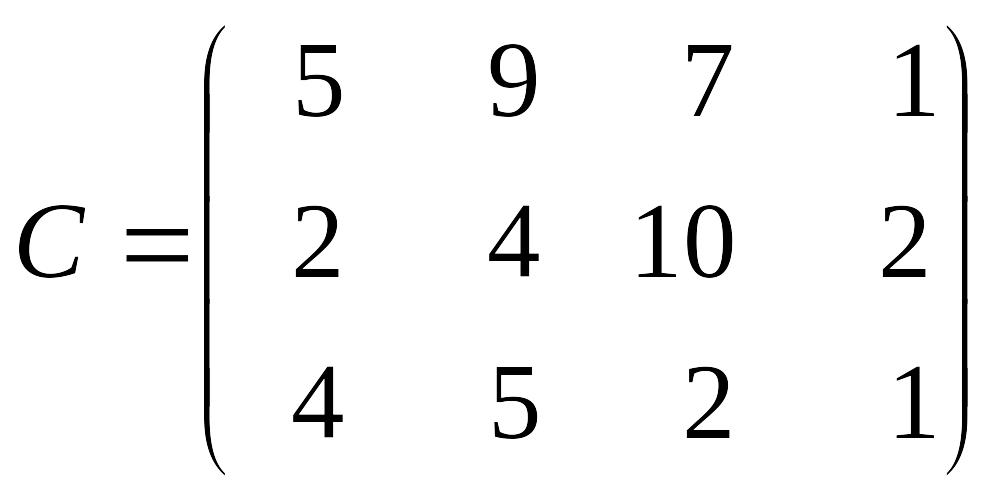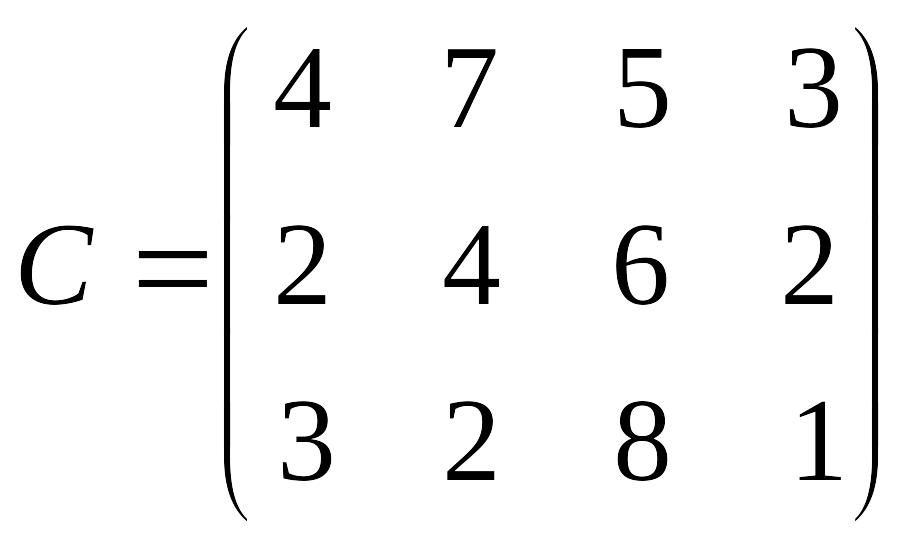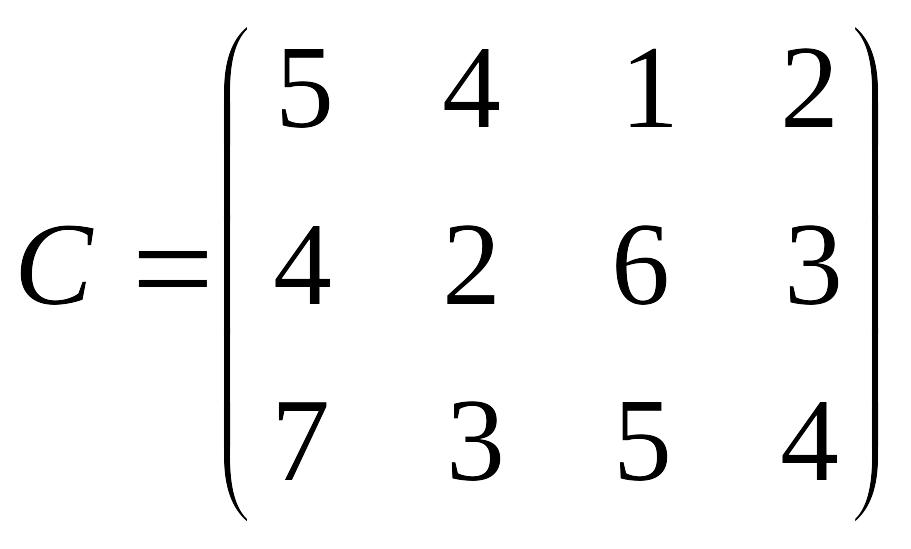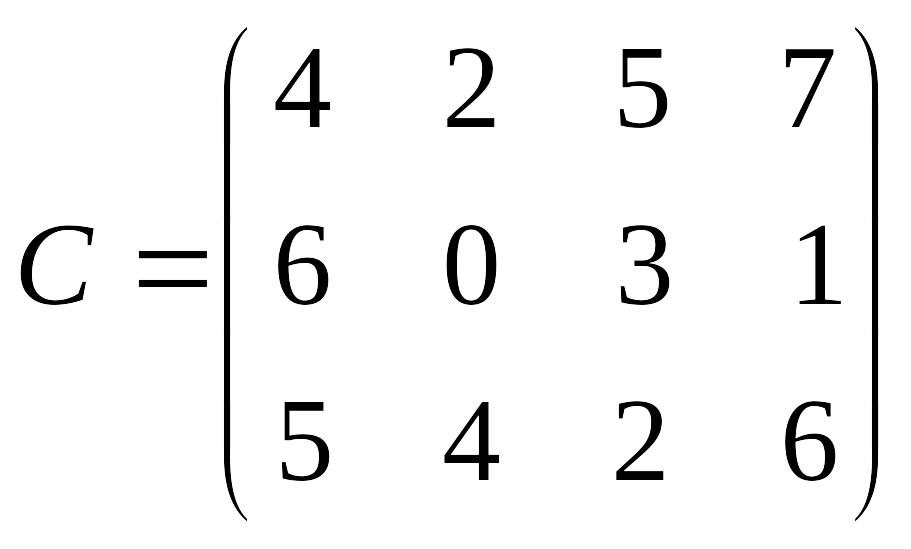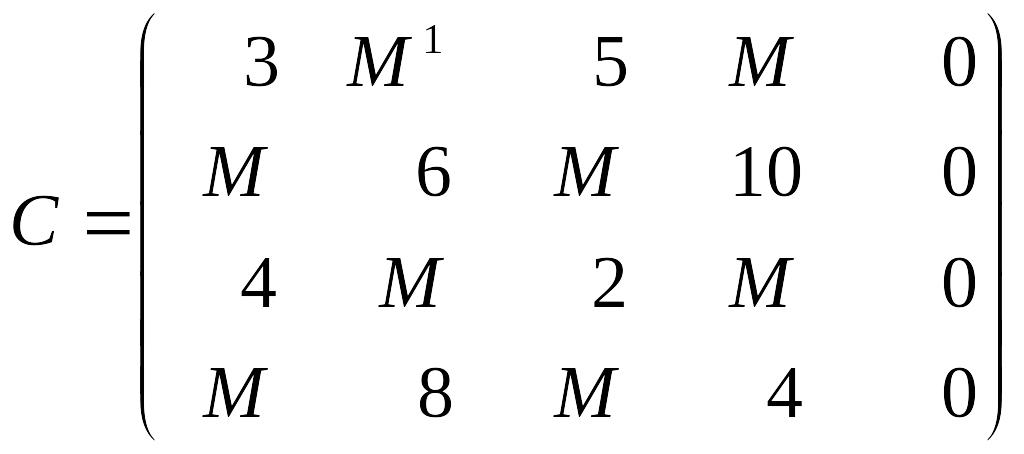- •Н.К. Максишко т.В. Заховалко с.С. Чеверда оптимізаційні методи та моделі
- •1 Мета та призначення лабораторного практикуму
- •2 Завдання, що мають вирішуватися за допомогою лабораторного практикуму та навички, які мають набути студенти в процесі виконання робіт
- •3 Методичні поради до виконання роботи Вимоги до оформлення та структури роботи
- •Перевірка роботи та вимоги до захисту роботи
- •4 Зміст завдань лабораторних робіт
- •Лабораторна робота № 4 Метод потенціалів розв’язування транспортної задачі
- •Лабораторна робота №5 Двоїстість та її застосування в економічному аналізі
- •Лабораторна робота №8 Сітьове планування та управління
- •Лабораторна робота №9 Застосування методу динамічного програмування для розв’язання задачі про розподіл капіталовкладень
- •5 Контрольні теоретичні питання Лабораторна робота №1 Побудова математичних моделей економічних задач
- •Лабораторна робота №2 Графічний метод розв’язування задачі лінійного програмування
- •Лабораторна робота №3 Симплекс-метод розв’язування задачі лінійного програмування
- •Лабораторна робота №4 Метод потенціалів розв’язування транспортної задачі
- •Лабораторна робота №5 Двоїстість та її застосування в економічному аналізі
- •Лабораторна робота №6 Угорський метод розв’язання задачі про призначення
- •Лабораторна робота №7 Транспортні мережі. Задача про максимальний потік
- •Лабораторна робота №8 Сітьове планування та управління
- •Лабораторна робота №9 Застосування методу динамічного програмування для розв’язання задачі про розподіл капіталовкладень
- •6 Перелік рекомендованої літератури
- •7 Короткі теоретичні відомості та методичні вказівки, що необхідні для виконання лабораторних робіт
- •Лабораторна робота №1
- •Побудова математичних моделей економічних задач
- •Хід роботи.
- •Лабораторна робота №2 Графічний метод розв’язування задачі лінійного програмування Хід роботи.
- •Лабораторна робота № 3 Симплекс-метод розв’язування задачі лінійного програмування Хід роботи.
- •Лабораторна робота №4 Метод потенціалів розв’язування транспортної задачі Хід роботи.
- •Лабораторна робота №7 Транспортні мережі. Задача про максимальний потік. Хід роботи
- •Лабораторна робота №8 Елементи мережевого планування
- •Лабораторна робота №9 Застосування методу динамічного програмування для розв’язання задачі про розподіл капіталовкладень
- •8 Завдання до лабораторних робіт Лабораторна робота № 1 Побудова математичних моделей економічних задач
- •Лабораторна робота №2 Графічний метод розв’язування задачі лінійного програмування
- •Лабораторна робота №3 Симплекс-метод розв’язування задачі лінійного програмування
- •Лабораторна робота № 4 Метод потенціалів розв’язування транспортної задачі
- •Лабораторна робота № 5 Двоїстість та її застосування в економічному аналізі
- •Лабораторна робота №6 Угорський метод розв’язання задачі про призначення
- •Лабораторна робота №7 Транспортні мережі. Задача про максимальний потік
- •Лабораторна рота № 8 Сітьове планування та управління
- •Індивідуальне завдання Економічний аналіз задач лінійного програмування
- •Приклад
- •Завдання
- •Термінологічний словник
Лабораторна робота №2 Графічний метод розв’язування задачі лінійного програмування
Завдання 1
Розв’язати задачу лінійного програмування графічним методом при числі змінних n = 2.
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
Лабораторна робота №3 Симплекс-метод розв’язування задачі лінійного програмування
Розв’язати задачу лінійного програмування симплекс-методом.
Перевірити отриманий розв’язок, розв’язавши задачу лінійного програмування за допомогою Microsoft EXCEL for WINDOWS.
1
|
2
|
|
|
3
|
4
|
|
|
5
|
6
|
|
|
7 |
8 |
|
|
9 |
10
|
|
|
11 |
12 |
|
|
13
|
14
|
|
|
15 |
16 |
|
|
17 |
18 |
|
|
19 |
20 |
|
|
21
|
22 |
|
|
23 |
24
|
||
25 |
26 |
||
27 |
28 |
||
29 |
30 |
||
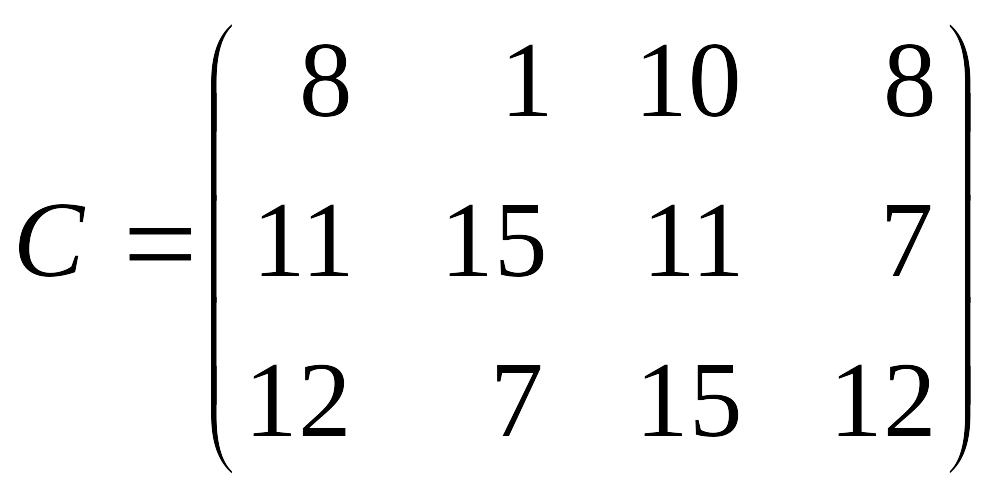
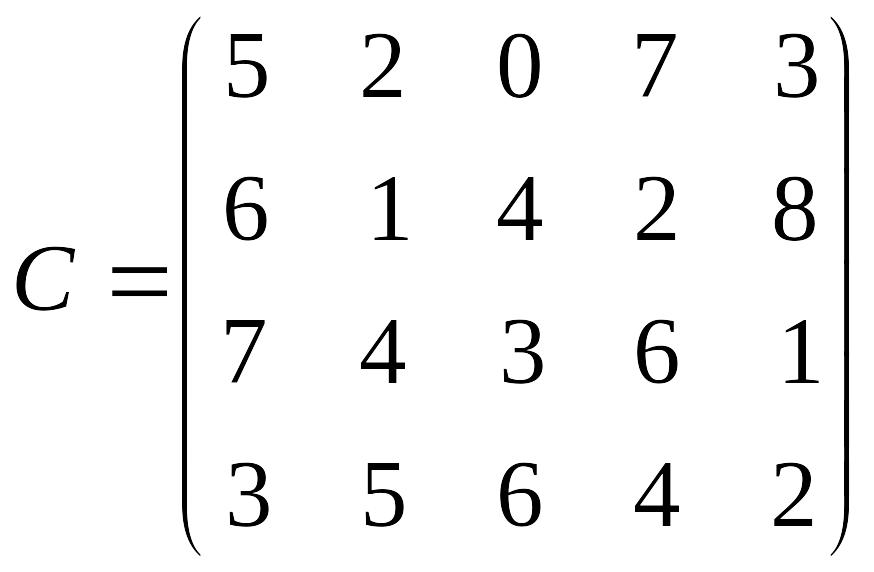
Лабораторна робота № 4 Метод потенціалів розв’язування транспортної задачі
Розв’язати транспортну задачу методом потенціалів.
Перевірити отриманий розв’язок, розв’язавши транспортну задачу за допомогою Microsoft EXCEL for WINDOWS
1
A=(30,50,20) B=(15,15,40,30) |
2
A=(40,30,35) B=(20,34,16,10,15) |
|
3
A=(150,250,300,300) B=(100,400,400,100) |
4
A=(70,80,80,20) B=(60,65,75,50) |
|
5
A=(100,150,250,500) B=(100,400,200,300) |
6
A=(250,300,350,150) B=(400,200,200,200) |
|
7
A=(70,120,20,40) B=(30,70,50,100) |
8
A=(80,40,160,120) B=(75,125,60,140) |
|
9
A=(300,150,350,200) B=(450,400,50,100) |
10
A=(50,30,40,20) B=(25,35,45,35) |
|
11
A=(45,30,50,70) B=(60,40,35,65) |
12
A=(60,140,160,140) B=(200,100,80,150) |
|
13
A=(60,140,160,140) B=(200,100,80,150) |
14
A=(100,400,70) B=(600,400,200) |
|
15
A=(350,650,500) B=(250,250,400,600) |
16
A=(900,300,400) B=(700,300,200,400)
|
|
17
A=(900,300,400) B=(700,300,200,400) |
18
A=(60,70,30,40) B=(80,80,40) |
|
19
A=(500,600,900) B=(450,350,550,650) |
20
A=(250,750,500,300) B=(350,450,400,600) |
|
21
A=(50,70,80) B=(60,40,90,10) |
22
A=(30,130,180) B=(80,60,80,20) |
|
23
A=(600,400,350) B=(400,250,200,500) |
24
A=(400,300,300) B=(200,250,300,250) |
|
25
A=(600,400,700,300) B=(600,400,400,300,300) |
26
A=(400,300,240,80) B=(300,100,240,200,180) |
|
27
A=(700,500,200,300) B=(500,400,100,150,200,300) |
28
A=(400,600,1000,1000) B=(700,700,700,700,200) |
|
29
A=(200,200,200,200) B=(190,190,190,190,40) |
30
A=(180,220,280,320) B=(460,180,260,160,240) |
|