Лабораторна робота №9 Застосування методу динамічного програмування для розв’язання задачі про розподіл капіталовкладень

Корпорація об’єднує чотири підприємства. Необхідно розподілити капіталовкладення в об’ємі k=200 тис. грн. між цими підприємствами на єдиний плановий період так, щоб в результаті забезпечити найбільший загальний по корпорації приріст продукції. При цьому вiдомi функції приросту продукції кожного підприємства (виражені у відносних одиницях) за умови виділення підприємству капіталовкладень в об’ємі тис. грн. Вихідні дані задачі наведені в табл.9.1.

Таблиця 9.1 – Вихідні дані

Капіталовловкладення тис. грн.	Приріст випуску продукції (у відносних одиницях)
0	0	0	0	0
50	25	30	36	28
100	60	70	64	56
150	100	90	95	110
	140	122	130	142

За змістом задачі розрахунки зведуться до перебору усіх можливих варiантiв розподілення капіталовкладень k=200 тис. грн. мiж чотирма підприємствами. Так як існують дані тільки за окремими дискретними значеннями об’ємів капіталовкладень ( = 50, 100, 150, 200 тис. грн.), то кiлькiсть варiантiв скінчена i легко розраховується.

Наприклад: якщо 200 тис. грн. розподілити мiж підприємствами нарівно по 50 тис. грн., то будемо мати (як видно з табл.1) такий загальний приріст продукції:

Очевидно, можливі i інші варіанти розподілення, які забезпечують вiдповiдний приріст продукції. Пошук оптимального (такого, забезпечує максимальне значення суми приростів продукції) варіанту розподілення капіталовкладень організуємо за допомогою використання функціональних рівнянь Беллмана. Попередньо зауважимо, що якщо підприємству капіталовкладення не виділяються, тобто , то приросту продукції немає, тобто .

Методика даного розрахунку буде складатися в тому, що при першому проході методу динамічного програмування формується множина умовно-оптимальних розв’язків таким чином: спочатку розглядається найкращий ефект від вкладення всіх заданих об’ємів коштів в одне підприємство, потім в два, потім – в три (третє та перші два) i, нарешті, на останньому етапі – в чотири (четверте та перші три) підприємства. При другому проході методу формується оптимальний розв’язок – розподіл капіталовкладень.

I етап. Розглядаємо перше підприємство – його функцію приросту продукції . Позначимо – максимальний приріст продукції на окремо взятому першому пiдприємствi, якщо йому виділити капіталовкладення . Будемо вважати

, (1)

так як ми маємо монотонний рiст приросту продукції в залежності вiд видiлених капiталовкладень, то з нерiвностi витiкає . Отже, для окремо взятого першого пiдприємства можна записати

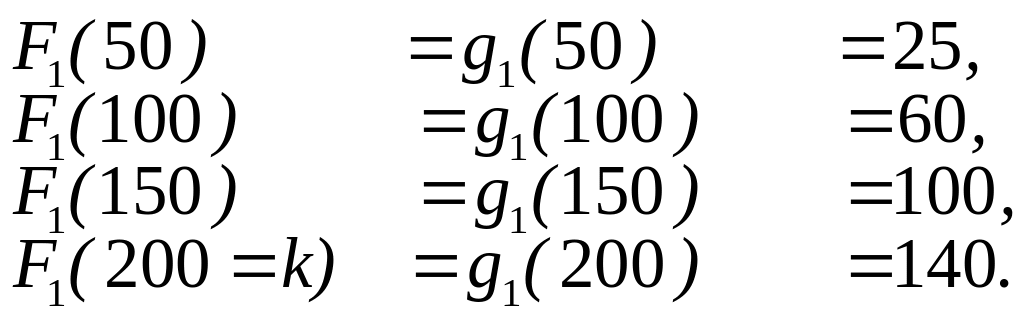
II етап. Необхiдно визначити найкращий розподiл капiталовкладень, якщо вони видiляються першому i другому пiдприємствам. При цьому враховуємо найкращий ефект вiд видiлення капiталовкладень першому пiдприємству. Позначимо – найбiльший прирiст продукцiї вiд розподiлення капiталовкладень мiж першим i другим пiдприємствами. Згiдно методики Беллмана:

. (2)

Проведемо розрахунки по цiй формулi для можливих значень видiлених капiталовкладень, тобто для 50, 100, 150, 200 тис. грн.

Оскiльки згiдно даних з табл. 1 аргумент може приймати лише деякi дискретнi значення, то на вiдрiзку вiд 0 до 50 для змiнної можливi лише два значення: 0 i 50, тому

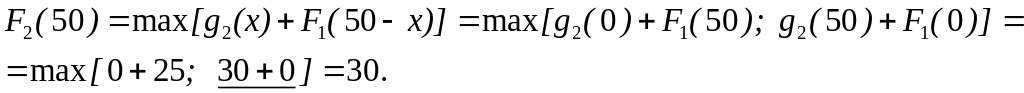
Пiд знаком максимуму пiдкреслено той член, який надає максимум: . Це . Вiн означає, що другому пiдприємству слiд видiлити 50 тис. грн. капiталовкладень, а першому не видiляти зовсiм. Проiлюструємо це умовною дiаграмою: в тому випадку, якщо першим двом пiдприємствам видiляється 50 тис. грн., то цi грошi слiд повнiстю вiддати другому пiдприємству (рис.9.1).

50 тис. грн. 

1 підпр.

2 підпр.

 50 тис. грн. 

Рисунок 9.1 – Умовно-оптимальний розподіл

В такiй ситуацiї припускається, що 150 тис. грн.( k--50 = 200 – 50 =150), які залишилися, деяким способом розподiленi мiж третiм i четвертим пiдприємствами. При розрахунку оцiнюється найкращій вибір при умові видiлення 50 тис. грн. першому i другому підприємствам (гіпотеза : «що…, якби…»).

Аналогiчно визначаємо вiд iнших видiляємих капiталовкладень, а саме

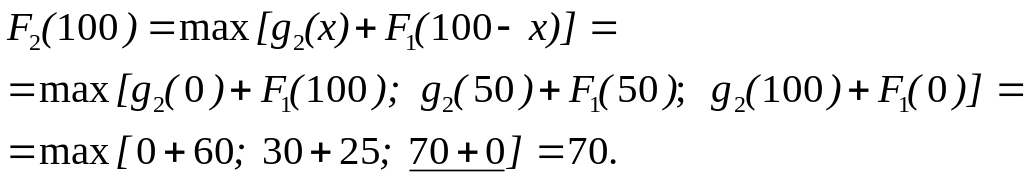
Найкращому ефекту вiдповiдає дiаграма на рис.9.2.

 100 тис.грн 

1 підпр.

2 підпр.

 100 тис. грн. 

Рисунок 9.2 – Умовно-оптимальний розподіл

При розподiлі 100 тис. грн. мiж першим i другим пiдприємствами слiд 100 тис. грн. видiлити другому пiдприємству. При цьому прирiст продукцiї буде 70 відн. од.:

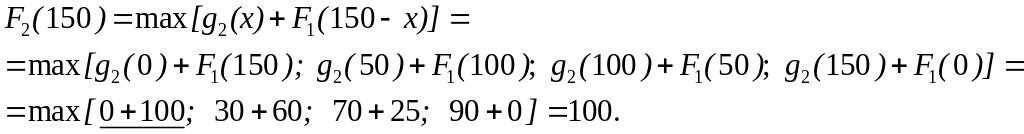
Таким чином з’ясували, що при видiленi 150 тис. грн. першому i другому пiдприємствам слiд усi 150 тис. грн. вiддати першому пiдприємству (рис.9.3).

150 тис. грн. 

1 підпр.

2 підпр.

 150 тис. грн. 

Рисунок 9.3 – Умовно-оптимальний розподіл

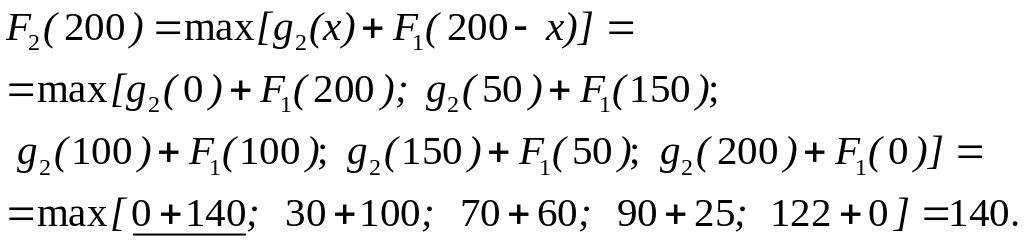
Діаграма розподiлення приведена на рис.9.4.

200 тис. грн. 

1 підпр.

2 підпр.

 200 тис. грн. 

Рисунок 9.4 – Умовно-оптимальний розподіл

III етап. Необхідно визначити найкращi варiанти капiталовкладень, якщо вони будуть видiлятися першому, другому i третьому пiдприємствам разом. Розраховуючи найкращий ефект для цього етапу , будемо вважати, що розподіл здійснюється між третім та першими двома підприємствами разом, а тому будемо спиратися на отриманi значення для :

(3)

З конкретних розрахункiв отримаємо

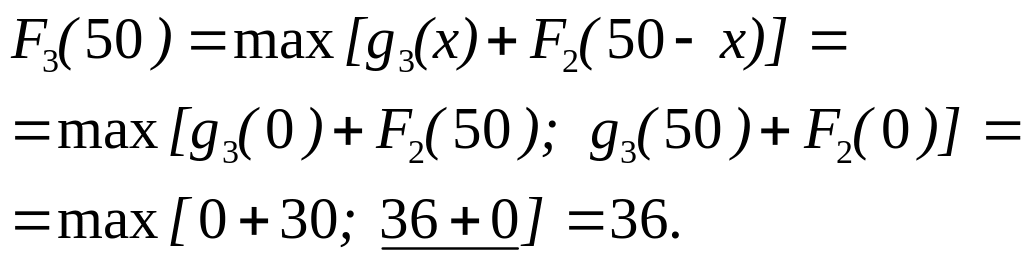
при дiаграмi розподiлу, що представлена на рис.9.5.

50 тис. грн. 

1 підпр.

2 підпр.

3 підпр.

50 тис. грн. 

Рисунок 9.5 – Умовно-оптимальний розподіл

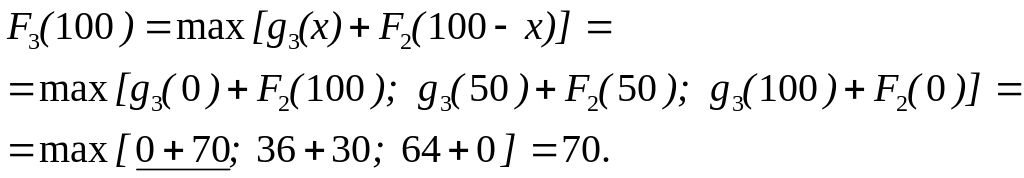
Максимальний ефект приносить член , який означає, що третьому пiдприємству капiталовкладень видiляти не треба, а першим двом потрiбно видiлити 100 тис. грн. (відповідна діаграма на рис.9.6).

100 тис. грн. 

1 підпр.

2 підпр.

3 підпр.

100 тис. грн. 

Рисунок 9.6 – Умовно-оптимальний розподіл

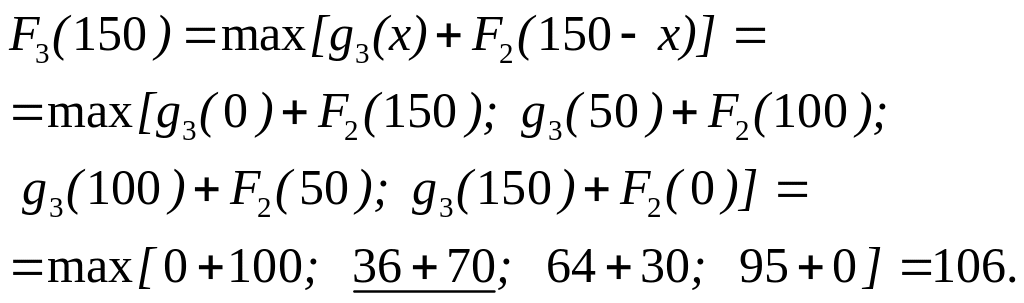
Максимальний ефект має додаток , тому слiд при розподiленнi 150 тис. грн. мiж першими трьома пiдприємствами вiддати 50 тис. грн. третьому пiдприємству, а 100 тис. грн. розподiлити між першими двома (рис.9.7).

150 тис. грн. 

1 підпр.

2 підпр.

3 підпр.

100 тис. грн.  50 тис. грн. 

Рисунок 9.7 – Умовно-оптимальний розподіл

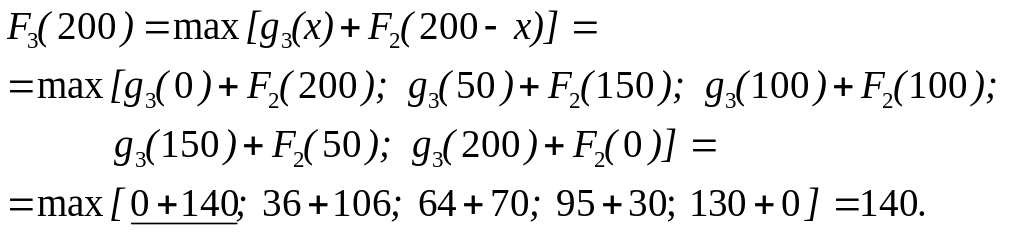
Максимальний член вказує, що у випадку видiлення 200 тис. грн. першим трьом пiдприємствам, третьому пiдприємству капiталовкладень не слід видiляти, а видiлити їх першому i другому. Дiаграма розподiлу подана на рис.9.8.

200 тис.грн.

1 підпр.

2 підпр.

3 підпр.

200 тис.грн.

Рисунок 9.8 – Умовно-оптимальний розподіл

IV етап. Необхідно оптимально розподiлити капiталовкладення вже мiж всiма чотирма пiдприємствами. При цьому згідно принципу занурення розрахунки ведуться за умови розподілу між четвертим підприємством та першими трьома. Необхiдно знайти

(4)

На цьому етапi немає сенсу розраховувати , та , а достатньо одразу визначити . Отже

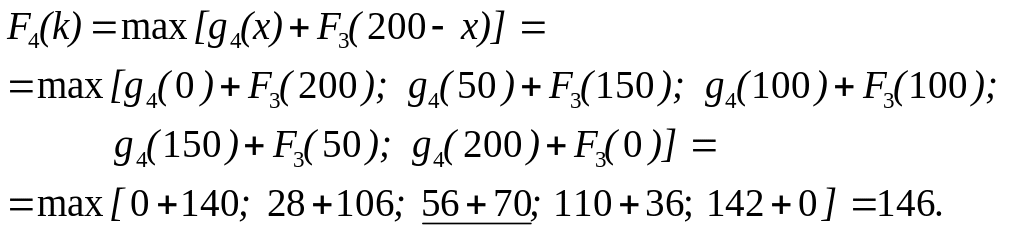
Максимальний член iнформує про те, що четвертому пiдприємству слiд видiлити 150 тис. грн. а першим трьом разом – 50 тис. грн. (рис.9.9). На цьому перший прохід методу завершено.

200 тис. грн.

1підпр.

2 підпр.

3 підпр.

4 підпр.

 50 тис. грн.   150 тис. грн. 

Рисунок 9.9 – Умовно-оптимальний розподіл

В результаті отримана множина умовно-оптимальних розв’язків задачі і оптимальне значення цільової функції – 146 відн. одиниць продукції забезпечить оптимальний розподіл капіталовкладень у корпорацію.

Для отримання розв’язку задачі виконаємо другий прохід методу (зворотній) і сформуємо оптимальний розподіл на основі отриманих на першому проході результатів.

Максимальне значення (рис.9) отримано за участю умовно-оптимального розв’язку (додатка) , якому відповідає рис.16. В свою чергу значення враховує значення . З урахуванням отриманих вище розв’язків та їх діаграм отримуємо заключну діаграму розподілу (рис.9.10).

200 тис. грн.

1підпр.

2 підпр.

3 підпр.

4 підпр.

 50 тис. грн.  150 тис. грн. 

Рисунок 9.10 – Оптимальний розподіл капіталовкладень в об’ємі  тис. грн. у 4 підприємства корпорації

Оптимальний розподіл полягає у виділенні 50 тис. грн. третьому підприємству, 150 тис. грн. – четвертому. Першому i другому підприємствам капіталовкладення виділяти не вигідно.

При такому розподiлі капіталовкладень отримаємо максимальний приріст продукції в 146 відн. од.