Лабораторна робота №7 Транспортні мережі. Задача про максимальний потік. Хід роботи

1. Побудувати початковий допустимий план-потік. Рішення можна почати, наприклад, з нульового потоку.

2. Перевірити, чи немає ненасичених шляхів, що ведуть з S в S’. Якщо вершина S’ не потрапила до множини вершин S, досяжних по ненасиченим ребрам з S, то побудований потік максимальний. Задача вирішена. Якщо вершина S’ потрапила до множини S, то потік можна збільшити.

3. Відокремити шлях, складений з ненасичених ребер, який веде з S в S’. Збільшити потік цього шляху на величину . Перейти до нового потоку, збільшеного на , і т.д.

Задача

Розглянемо графічний спосіб розв’язання задачі:

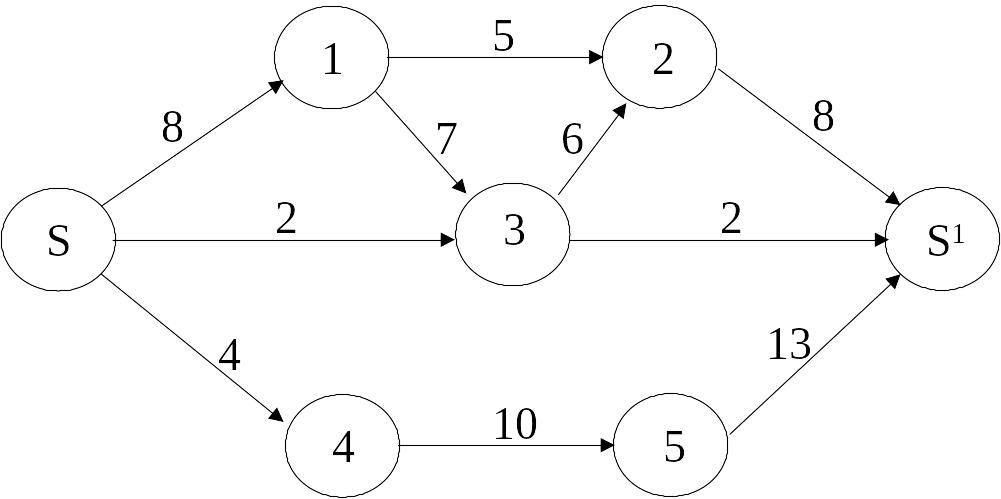
Побудуємо початковий допустимий потік Хо, для цього розглянемо, наприклад, шляхи

“1” S-1-3-2-S’ min{10,7,6,8}=6

“2” S-4-5-S’ min{4,10,13}=4

По шляху “1” пропустили min{10,7,6,8}=6

По шляху “2” пропустили min{4,10,13}=4

Отримуємо потік Хо величиною =10 одиниць.

Мережа, відповідна потоку Хо, зображена нижче. При цьому числа над ребрами означають: без дужок – залишена пропускна можливість, у дужках – величина перевезеного вантажу, тобто величина потоку через ребро.

Пунктиром зображено насичені ребра, тобто ребра, потік через які дорівнює їхньої пропускній можливості.

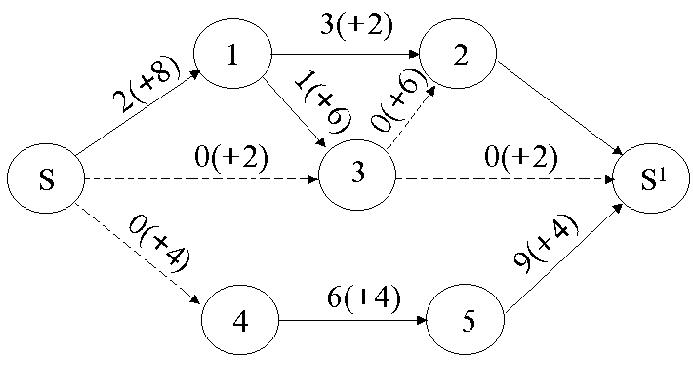
2. Перевіряємо, чи нема ненасичених шляхів. Такі шляхи є тому, що початковий потік можна збільшити. Для цього обираємо шляхи “3”, “4”.

“3” S1-2S’ min{4,5,2}=2

“4” S3S’ min{2,2}=2

По шляху пропускаємо потік величиною 2 одиниці, а по шляху

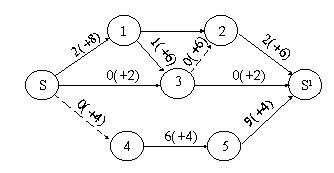
також 2 одиниці. Отримуємо потік у мережі величиною одиниць.

Так як більше ненасичених шляхів з вершин S в S’ немає, то отриманий потік є максимальним и задача вирішена.

Лабораторна робота №8 Елементи мережевого планування

При плануванні і оперативному управлінні складними комплексами робіт, об'єднаних спільністю мети, з успіхом використовуються їх графічні моделі – мережеві графіки (мережі).

Якщо елементам графа поставити у відповідність деякі параметри, то отримаємо мережу.

Параметри можуть бути задані вершинами або (і) дугами графа.

Орграф перетворюється в мережу, якщо кожній вершині U_i поставлено у відповідність деяке число d_i, зване інтенсивністю вершини, а кожній дузі (V_i, V_j) – невід'ємне число r_ij, зване її пропускною спроможністю.

Поняття мережі лежить в основі системи мережевого планування та управління (СПУ).

Мережевий графік – це орієнтований граф без контурів, дуги якого мають одну або кілька числових характеристик.

Дугами зображуються роботи, а вершинами – події.

Робота – будь-який трудовий процес або дія, що супроводжуються витратами часу і ресурсів.

Під роботами маються на увазі: не тільки реальні господарські або технологічні процеси, що вимагають витрат часу і ресурсів, а й процеси, що споживають тільки час (сушка матеріалів, затвердіння бетону тощо).

На мережевих графіках фіктивні роботи зазвичай зображуються пунктирними стрілками (- →).

Подія – підсумок того чи іншого процесу, проміжний або остаточний результат виконання однієї або кількох попередніх робіт, який дозволяє розпочати наступні.

Подія відбувається тоді, коли закінчені всі попередні роботи. Вона стає передумовою для початку наступних за нею робіт. Звідси, подія має властивість «зшивання» попередніх робіт з подальшими. Передбачається, що подія не має тривалості і здійснюється миттєво.

Кожна подія, що включена в мережевий графік, має бути повно, точно і всебічно визначена, її формулювання повинно включати результат виконання безпосередньо попередніх робіт.

Події зображуються точками, колами, ромбами. Це вершини відповідного графа. Подія вважається доконаною тільки тоді, коли буде закінчена найдовша з усіх вхідних у неї робіт.

Внутрішній взаємозв'язок між роботами в графіку визначається дотриманням основного правила: всі роботи взаємопов'язані. Початок наступної обумовлено закінченням попередньої. Не може бути події, настання якої не означало б закінчення, принаймні, однієї роботи і початок іншої. Виняток становлять вихідна і завершальна події.

Шлях – це будь-яка безперервна логічна (технологічна) послідовність робіт від вихідного до завершального пункту, тобто від початку розробки до кінцевої мети.

В результаті складання та аналізу мережевого графіка виявляється такий шлях, сумарна тривалість робіт на якому буде максимальною – так званий критичний шлях – він визначає (обумовлює) час, необхідний для виконання всіх робіт, включених в мережевий графік.

Всі роботи, що лежать на критичному шляху, також є критичними. Вони – потенційно вузьке місце плану. У мережі можна знайти кілька критичних шляхів.

Види мережних моделей

Можуть бути використані 3 основних види мережевих моделей:

1) у термінах подій, в яких події зображуються вершинами графа, а дуги показують взаємозв'язок окремих подій;

2) у термінах робіт, в яких роботи будуть вершинами графа, а дуги показують взаємозв'язок окремих робіт;

3) в термінах робіт і подій, – в яких роботи – це дуги, а події – вершини.

За кількістю завершальних подій мережеві графіки поділяються на одно-і багатоцільові.

Існує кілька загальних правил побудови мережевих графіків:

а) від початку до кону (від вихідної події до завершального)

б) від середини до кінця і початку

в) від кінця до початку.

Найчастіше – найбільш поширений метод – а) – від початку до кінця, зліва направо.

Кожна подія з великим порядковим номером показується правіше попереднього номера.

Стрілки можуть бути довільної довжини і напряму, але обов'язково розташовуватися зліва направо. (По можливості уникати взаємного перетину стрілок).

Приступаючи до складання мережі, необхідно встановити, які роботи:

• повинні бути завершені раніше, ніж почнеться подана (попередня робота);

• можуть бути розпочаті після завершення поданої роботи;

• можуть виконуватися одночасно з поданою роботою.

При побудові мережі обов'язково складається чорновий варіант.

Далі її можна впорядкувати. При цьому в неї часто доводиться додавати так звані «забуті» роботи.

Складання мережевих графіків ведеться в 3 етапи:

I етап – формування завдання, що визначає кінцеву мету розробки. Крім основної (кінцевої) мети, слід виділити і проміжні, які повинні бути взаємопов'язані як по послідовності, так і за результатами досягнення. Проміжні цілі, визначають рівень виконання програми, і є приватними завданнями, які потрібно вирішити для досягнення основної мети.

II етап – полягає в складанні структурної схеми розробки, або «Дерева розробки», які повинні наочно показувати обсяг і етапи робіт.

Для складання структурної схеми програма ділиться на підсистеми, підсистеми – на комплекси, комплекси – на елементи.

III етап – складання переліку робіт в кожній ланці і формування їх тимчасових оцінок.

Визначення тривалості робіт.

Після визначення орграфа, що відображає послідовність і взаємозв'язок робіт необхідно визначити тривалість кожної.

Достовірність розрахункових параметрів мережного графіка обумовлюється вірогідністю вихідних даних.

Відома, тривалість виконання робіт тісно пов'язана з використанням ресурсів (> ресурсів, як правило, → <тривалість роботи).

Тривалість ведення робіт оцінюють найбільш компетентні фахівці – експерти, виконавці з використанням нормативно-довідкової бази та з урахуванням наявних фінансових та матеріальних ресурсів.

При оцінці параметрів мережного графіка на початковій стадії встановлюються тільки тривалості робіт, а не терміни їх виконання.

Розрахунок параметрів мережного графіка

Тривалість критичного шляху є головним параметром мережевого графіка.

Всі шляхи, відмінні за тривалістю від критичного, розташовують резервами часу. Повним резервом часу будь-якого некритичного шляху називається різниця між довжиною критичного і даного некритичного шляху.

Позначається R (L): R (L) = t-t (L).

Питання: чи можна використовувати резерв часу шляху на його роботах без перевищення довжини критичного шляху?

При аналізі можуть представитися наступні випадки:

1. Некритичний шлях не перетинається з критичним і не має робіт, що належать останньому. У цьому випадку:

а) якщо роботи некритичного шляху не належать іншим шляхам більшої довжини, то його резерв часу може бути використана повністю або частинами на будь-якій роботі;

б) якщо деякі роботи некритичного шляху належать шляхах більшої довжини, то його резерв часу може бути витрачений в повному розмірі лише для робіт, які не належать шляхах більшої довжини. Для інших він може бути витрачено тільки в межах резервів часу максимальних шляхів робіт.

2. Якщо некритичний шлях має окремі роботи на критичному, а інші не належать шляхах більшої довжини, то його повний резерв часу може бути використана повністю або частинами на будь-якій його роботі, окрім критичних. Якщо деякі роботи, відмінні від критичних, належать шляхах більшої довжини, то в повному розмірі резерв часу може бути витрачена тільки для робіт, які не належать шляхах більшої довжини. В іншому випадку резерв часу може бути використаний в межах резервів часу максимальних шляхів.

3. Якщо некритичний шлях перетинається з критичним і має після перетину некритичні роботи, то його резерв часу в повній величині можна витрачати без перевищення довжини критичного шляху ні на одній з належних йому робіт.

Подія здійснюється в момент, коли попередні роботи виконані. Тобто може бути кілька шляхів, що передують даній події, то ранній час звершення події i – t (i) – визначиться тривалістю максимального шляху, що передує події, тобто

t (i) = t [L (i)] (1)

Відповідно, щоб знайти ранній час звершення події, потрібно знати критичний шлях орієнтованого подграфа, що складається з безлічі шляхів, що передують даній події (1).

Як знайти час пізнього звершення події i: t (i)?

Кожна подія має здійснюється в такий термін, щоб залишилося достатньо часу для виконання робіт, наступних за цією подією.

Таким шляхом буде той наступний, який має максимальну тривалість L (i). Самий пізній з допустимих термінів звершення події в сумі з тривалістю виконання наступних робіт не повинен перевищувати довжини критичного шляху: t (i) + t [L (i)] = t .

Звідси:

t (i) = t – t [L (i)] (2)

тобто пізній термін звершення події обчислюється як різниця між тривалістю критичного шляху і тривалістю максимального з наступних за подією i шляхів (2).

Тобто при обчисленні критичного шляху методом динамічного програмування у кожної вершини графа варто максимальний час, необхідне для виконання робіт, наступних за цією подією, то розрахунок пізнього часу звершення події не становить труднощів.

Очевидно, для подій, що лежать на критичному шляху, t (i) =t(i).

Знаючи ранні та пізні терміни звершення подій мережного графіка, легко з’ясувати резерв часу кожного з них. Різниця між найбільш пізнім і найбільш раннім з можливих термінів називається резервом часу цієї події, тобто

R (i) = t (i) – t (i) (3)

Резерв часу події i показує максимальне допустиме час, на який можна відсунути момент його звершення, не викликаючи збільшення критичного шляху. Події критичного шляху резерву часу не мають.

Враховуючи, що t [L (i)] + t [L (i)] = мах t [L (i)] – є тривалість шляху максимальної довжини, що проходить через подію, одержимо:

R (i) = t-мах t [L (i)] = R [мах L (i)] (4)

Звідси резерв часу будь-якої події i дорівнює повного резерву часу максимального шляху, що проходить через цю подію (4).

Приклад:

За даними необхідно:

1. Побудувати мережеву модель розрахувати тимчасові параметри подій (на малюнку) та робіт (в таблиці)

2. Визначити критичні шляхи моделі

3. Оптимізувати мережеву модель за критерієм «min виконавців»

Назва роботи	Нормальна тривалість	Кількість виконавців
A	8	2
B	6	2
C	6	1
D	8	4
E	3	1
F	4	7
G	7	2
M	7	2
I	12	3
J	9	5
K	5	7

1.A, E, F-вихідні роботи проекту, які можна починати одночасно;

2.Роботи B та I починають відразу по закінченню роботи F;

3. Робота J слідує за E, а робота C- за A;

4.Робота H та D слідує за B, але не можуть починатися поки не закінчена C;

5.Робота K слідує за I;

6. Робота G починається після закінчення H та J.

Рішення

Побудуємо послідовність виконання робіт

1. та 2)

Рисунок 8.1 – Визначення критичного шляху

Таблиця 8.1 – Визначення критичного шляху

Код роботи	t(i,j)	Трн	Тро	Тпн	Тпо	Rп	Rc
1 2	3	0	3	0	12	9	0
1 3	8	0	8	0	8	0	0
1 4	4	0	4	0	8	4	0
2 7	9	3	12	12	21	9	9
3 6	6	8	14	8	14	0	0
4 6	6	4	10	8	14	4	4
4 5	12	4	16	4	23	7	0
5 8	5	16	21	23	28	7	7
6 7	7	14	21	14	21	0	0
6 8	8	14	22	20	28	6	6
7 8	7	21	28	21	28	0	0

Трн=Тр(i)

Тро=Тр(i)+t(i,j)

Tпн=Tр(j)-t(i,j)

Tпо=Тп(j)

Rп=Тп(j)-Tp(i)-t(i,j)

Rc=Tp(j)-Tp(i)-t(i,j)

З метою вирівнювання завантаження роботи 27; 46; 58 були зрушені відповідно на 1; 4; 6 днів. На 37рафіку ці зміни показані пунктирною лінією. Проведена оптимізація була основана на використанні вільних резервів робіт, тобто при зрушенні даних робіт, моменти початку наступних робіт залишились не змінними.

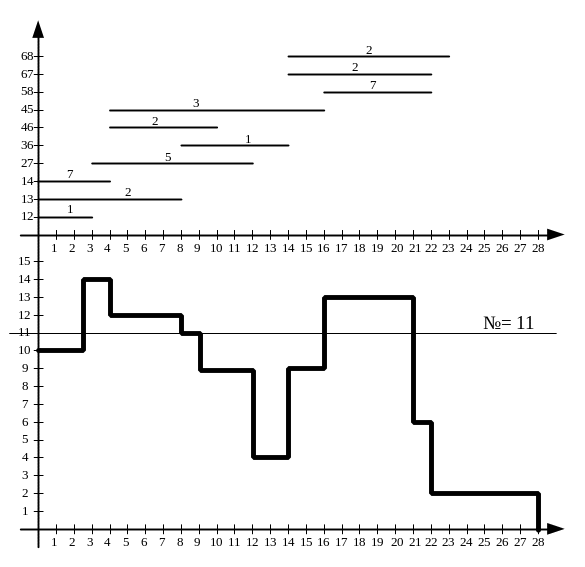
Рисунок 8.2 – Оптимізація процесу

Рисунок 8.3 – Оптимізація робіт