38. Преобразование Лежандра. Энтальпия

Другие термодинамические потенциалы можно получить с помощью преобразования Лежандра. В общем виде это выглядит следующим образом. Термодинамический потенциал L естественных переменных x, y, z, … имеет полный дифференциал dL = Xdx + Ydy + Zdz + … . Здесь X, Y, Z, … – функции переменных x, y, z, … . Преобразование Лежандра состоит в следующем. Вместо функции L и независимых переменных x, y, z, … вводятся новые переменные:

L   = L – Xx;  x, y, z, …  X, y, z, … . (38.1)

Тогда

d = – xdX + Ydy + Zdz + … . (38.2)

Таким образом можно ввести энтальпию:

H = U + pV (38.3)

(здесь x = V, X = – p, L = U,  = H). Естественные переменные для этого потенциала – энтропия S и давление p. Дифференциал энтальпии в силу уравнения (29.9) равен

dH = TdS + Vdp. (38.4)

Условием того, что он полный, является соотношение Максвелла (еще одно)

(T / p)_S = (V / S)_p. (38.5)

Его легко получить, если перейти к якобиану и воспользоваться калибровочным соотношением (35.4):

(T / p)_S = (T, S) / (p, S) = (p, V) / (p, S) = (V / S)_p.

Коэффициенты в выражении (38.4) для dH определяются через частные производные от H:

T = (H / S)_p =  T(S, p),  V = (H / p)_S  = V(S, p). (38.6)

Эту систему функций можно рассматривать как параметрическое задание термического уравнения состояния. Исключение параметра S приводит его к обычному виду. Внутренняя энергия находится из определения энтальпии (38.3):

U = H(S, p) – p  V(S, p) = U(S, p).

Исключение отсюда энтропии и давления (с помощью уравнений системы (38.6)) позволяет найти калорическое уравнение состояния. При желании можно получить другие термодинамические характеристики физической системы. Например:

c_p = (δQ / T)_p = T(S / T)_p = T / (T / S)_p = (H / S)_p / (²H / S ²)_p.

При изобарических процессах (dH)_p = T(dS)_p = δQ_p = c_pdT, откуда

c_p = (H / T)_p. (38.7)

Физический смысл энтальпии при изобарических процессах объясняет ее другие названия: тепловая функция, теплосодержание.

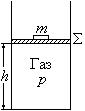
Рис. 16

Убыль энтальпии при адиабатических процессах равна работе расширенной системы, состоящей, например, в случае газа в цилиндре под поршнем, из газа и поршня с грузом массы m (рис. 16). Полная энергия E такой системы равна внутренней энергии U газа и потенциальной энергии груза mgh = pV (p = mg / Σ, V = Σh): E = U + pV = H. При адиабатических процессах расширенная система совершает работу за счет своей энергии:

δA_расш = – dE = – dH,  или – dH = δA_расш.