59. Равновесие между паром и конденсированной фазой

При исследовании равновесия между конденсированной фазой (жидкостью, кристаллом) и паром можно считать, что молярный объем пара много больше, чем молярный объем конденсированной фазы, и последним пренебречь. Уравнение Клапейрона–Клаузиуса в этом случае примет вид

dp / dT = λ / (TV_п).

Если при этом пар является достаточно разреженным, так что его можно считать идеальным газом, то V_п = RT / p и

dp / p = λ dT / (RT²). (59.1)

Зависимость λ от T может быть найдена приемом, аналогичным тому, что применялся при получении уравнения (58.1). Дифференцирование по T выражения (57.1) для λ дает

dλ / dT = ∆S + T(∆S / T)_p + T(∆S / p)_Tdp / dT =

= ∆S + ∆c_p – T(∆V / T)_p dp / dT .

С учетом уравнения Клапейрона–Клаузиуса (58.1) и того, что ∆V   V_п, а пар – идеальный газ,

dλ / dT = ∆S + ∆c_p – T (R / p) ∆S /V_п = ∆c_p.

Таким образом, скрытая теплота перехода при некоторой температуре T равна

λ = λ₀ + . (59.2)

Основным членом в выражении для λ (59.2) является первое слагаемое; второе добавляет слабую зависимость λ от T. Если λ приближенно считать постоянной, то интегрирование (59.1) приводит к

ln (p / p₀) = λ / R  (T₀^–1 – T ^–1)  и   p = A exp(– λ / (RT)).

Несложно проинтегрировать уравнение (59.1) и с учетом второго члена, когда ∆c_p  = const, при этом получится

ln (p / p₀) = λ / R  (T₀^–1 – T ^–1)  + ∆c_p / R  ln (T/T₀),

или

ln p = A – B / T + C ln T.

Это уравнение было получено Кирхгофом и широко используется для обработки экспериментальных данных.

60. Равновесие трех фаз

Простейшим примером, когда в равновесии находятся одновременно три фазы химически однородного вещества, является система, состоящая из твердой фазы, жидкости и пара (для H₂O это лед, вода и водяной пар). Однако большинство веществ имеет не одну, а несколько кристаллических модификаций. В связи с этим возможны такие варианты: в равновесии находятся две кристаллические и одна жидкая фазы, две кристаллические и газообразная фазы, три кристаллические фазы. Ради конкретности ниже рассматривается равновесие твердой, жидкой и газообразной фаз одного вещества.

При равновесном сосуществовании твердой фазы, жидкости и их пара должны выполняться три условия:

μ₁(p, T) = μ₂(p, T),  μ₂(p, T) = μ₃(p, T),  μ₃(p, T) = μ₁(p, T). (60.1)

Пусть первое из них выражает условие равновесия твердой и жидкой фаз, второе – жидкости и ее пара, третье – пара с твердой фазой. Каждому из этих условий на плоскости p, T отвечает кривая равновесия: первому – кривая плавления, второму – испарения и третьему – возгонки.

Одновременному выполнению трех условий (60.1) соответствует общая точка кривых равновесия, называемая тройной точкой (для нахождения ее параметров p и T имеются три уравнения: независимых уравнений два, третье есть следствие их).

Можно показать, что в тройной точке кривая возгонки идет круче кривой испарения. Действительно, из уравнения Клапейрона–Клаузиуса (58.1)

dp₁₃ / dT = λ₁₃ / (T(V₃ – V₁))  и  dp₂₃ / dT = λ₂₃ / (T(V₃ – V₂)).

Молярными объемами жидкой и твердой фаз можно пренебречь по сравнению с молярным объемом газообразной фазы, т. е. знаменатели в правых частях практически одинаковы. Из первого же начала термодинамики следует, что в тройной точке

λ₁₃ = λ₁₂ + λ₂₃ > λ₂₃.

Таким образом, dp₁₃ / dT  > dp₂₃ / dT .

p p0
	T0 T
Рис. 26

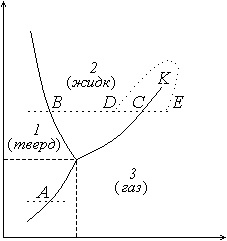
Диаграмма p, T имеет вид, показанный на рис. 26. Для воды параметры тройной точки следующие: p₀ = 4,58 мм рт. ст., T₀ = 273,16 К. С помощью диаграммы p, T можно судить о фазовых превращениях, которые будут происходить при том или ином процессе (по этой причине плоскость p, T называют диаграммой состояний). Так, при изобарическом подводе теплоты (ему отвечает прямая, параллельная оси T) твердое вещество будет испаряться, минуя жидкую фазу, если p < p₀ (точка A). Если же p > p₀ (но p < p_к), то твердое вещество будет вначале плавиться (точка B), а затем жидкость испаряться (точка C).