МИНИСТЕРСТВО образованиЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Ю.Я. Кацман Теория вероятностей, математическая статистика и случайные процессы
Издательство Томского политехнического университета 2011
УДК 519.2(075.8)
ББК 22.17я73
Кацман Ю.Я.
Теория вероятностей, математическая статистика и случайные процессы: учебное пособие / Ю.Я. Кацман; Национальный исследовательский Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2011. – 130 с.
Данное пособие предназначено для первоначального изучения теории вероятностей, математической статистики и случайных процессов. В нем изложены основные понятия, свойства и методы современной теории. Изложение теоретического материала сопровождается большим количеством примеров решения задач, представляющих практический интерес в различных областях науки и техники.
Пособие подготовлено на кафедре вычислительной техники, соответствует программе дисциплины и предназначено для студентов, обучающихся по направлению ООП 230400 «Информационные системы и технологии», профиль подготовки "Геоинформационные системы, Информационные системы в технологии в бизнесе".
УДК 519.2(075.8)
ББК 22.17я73
Рецензенты
Доктор физико-математических наук, профессор ТГУ Г.М. Кошкин
Кандидат физико-математических наук, доцент ТУСУР Н.Э. Лугина
© ГОУ ВПО НИ ТПУ, 2011
© Кацман Ю.Я., 2011
© Обложка. Издательство Томского политехнического университета, 2011
Учебное издание
КАЦМАН Юлий Янович
Теория вероятностей, математическая статистика и случайные процессы
Учебное пособие
Издано в авторской редакции
Научный редактор доктор технических наук, профессор В.Г. Спицын
Отпечатано в Издательстве тпу в полном соответствии с качеством предоставленного оригинал-макета
|
||
|
Национальный исследовательский Томский политехнический университет Система менеджмента качества Томского политехнического университета сертифицирована NATIONAL QUALITY ASSURANCE по стандарту ISO 9001:2008 |
|
Тел./факс: 8(3822)56-35-35, www.tpu.ru |
||
.
634050, г. Томск,
пр.
Ленина,
30
Оглавление
ВВЕДЕНИЕ 9
Раздел 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ 12
Глава 1. Основные понятия теории вероятностей 12
1.1. Элементы комбинаторики 12
1.2. Пространство элементарных событий. Случайные события 16
1.3. Статистическое определение вероятности 19
1.4 Классическая вероятностная схема 20
1.5. Аксиоматическое построение теории вероятностей 23
1.6. Геометрическое определение вероятности 24
Глава 2. Основные теоремы теории вероятностей 27
2.1. Теорема сложения вероятностей несовместных событий 27
2.2. Теорема сложения вероятностей совместных событий 28
2.3. Независимость событий 30
2.4. Теорема умножения вероятностей 31
2.5. Формула полной вероятности 33
2.6. Теорема гипотез (Формула Байеса) 36
Глава 3. Повторение испытаний 38
3.1. Схема Бернулли 38
3.1.1. Обобщение схемы Бернулли 42
3.2. Теорема Пуассона (Закон редких событий) 43
3.3. Локальная теорема Муавра-Лапласа 44
3.4. Интегральная теорема Муавра-Лапласа 45
Глава 4. Случайные величины 47
4.1. Классификация случайных величин. Закон распределения дискретной случайной величины 47
4.1.1. Интегральная функция распределения 50
4.2. Непрерывная случайная величина, плотность распределения 51
4.2.1. Основные свойства плотности распределения 54
4.3. Характеристики положения случайной величины 56
4.4. Числовые характеристики одномерной случайной величины 58
4.5. Моменты случайной величины 60
Глава 5. Многомерные случайные величины 66
5.1. Многомерная случайная величина и закон ее распределения 66
5.2. Плотность вероятности двумерной случайной величины 69
5.2.1. Условная плотность распределения 73
5.3. Числовые характеристики системы случайных величин 75
Глава 6. Основные законы распределения 79
6.1. Нормальный (гауссов) закон распределения 79
6.1.1. Вероятность попадания на интервал 82
6.1.2. Свойства нормальной функции распределения 83
6.2. Распределение ("хи–квадрат") 86
6.3. Показательный (экспоненциальный) закон распределения 87
6.3.1 Числовые характеристики показательного распределения 88
6.3.2. Функция надежности 90
6.4. Распределение Парето 91
Глава 7. Закон больших чисел 93
7.1. Неравенство Чебышева 93
7.2. Теорема Чебышева 94
7.3. Обобщенная теорема Чебышева 96
7.4. Теорема Маркова 97
7.5. Теорема Бернулли 98
7.6. Центральная предельная теорема 99
Раздел 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 101
Глава 8. Основные понятия и задачи математической статистики 101
8.1. Выборочные распределения 103
8.1.1. Группирование данных, гистограмма, полигон 104
106
107
8.2. Статистическая (эмпирическая) функция распределения 107
8.3. Выборочные значения и оценка параметров. 109
8.3.1. Требования "хороших оценок" 110
Глава 9. Интервальное оценивание 112
9.1. Интервальная оценка математического ожидания при известной дисперсии 114
9.2 Интервальная оценка математического ожидания при неизвестной дисперсии 115
9.3. Интервальная оценка выборочной дисперсии 117
Глава 10. Статистические критерии 119
10.1. Проверка гипотез 120
10.2. Ошибки проверки гипотез 123
Раздел 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ 125
Глава 11. Основные понятия и модели случайных процессов 125
11.1. Классификация случайных процессов 126
11.2. Основные характеристики случайного процесса 127
11.2. Стационарные случайные процессы 131
11.3. Марковские случайные процессы 132
11.4. Потоки событий (Пуассоновские потоки) 136
11.5. Непрерывный марковский процесс. Уравнения Колмогорова 139
ЗАКЛЮЧЕНИЕ 142
Список литературы 142
ВВЕДЕНИЕ 6
Раздел 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ 8
Глава 1. Основные понятия теории вероятностей 8
1.1. Элементы комбинаторики 8
1.2. Пространство элементарных событий. Случайные события 12
1.3. Статистическое определение вероятности 15
1.4 Классическая вероятностная схема 16
1.5. Аксиоматическое построение теории вероятностей 19
1.6. Геометрическое определение вероятности 20
Глава 2. Основные теоремы теории вероятностей 22
2.1. Теорема сложения вероятностей несовместных событий 22
2.2. Теорема сложения вероятностей совместных событий 24
2.3. Независимость событий 25
2.4. Теорема умножения вероятностей 27
2.5. Формула полной вероятности 28
2.6. Теорема гипотез (Формула Байеса) 30
Глава 3. Повторение испытаний 33
3.1. Схема Бернулли 33
3.1.1. Обобщение схемы Бернулли 37
3.2. Теорема Пуассона (Закон редких событий) 38
3.3. Локальная теорема Муавра-Лапласа 39
3.4. Интегральная теорема Муавра-Лапласа 40
Глава 4. Случайные величины 41
4.1. Классификация случайных величин. Закон распределения дискретной случайной величины 41
4.1.1. Интегральная функция распределения 44
4.2. Непрерывная случайная величина, плотность распределения 45
4.2.1. Основные свойства плотности распределения 48
4.3. Характеристики положения случайной величины 50
4.4. Числовые характеристики одномерной случайной величины 52
4.5. Моменты случайной величины 54
Глава 5. Многомерные случайные величины 59
5.1. Многомерная случайная величина и закон ее распределения 59
5.2. Плотность вероятности двумерной случайной величины 62
5.2.1. Условная плотность распределения 66
5.3. Числовые характеристики системы случайных величин 67
Глава 6. Основные законы распределения 71
6.1. Нормальный (гауссов) закон распределения 71
6.1.1. Вероятность попадания на интервал 74
6.1.2. Свойства нормальной функции распределения 75
6.2.
Распределение
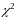("хи–квадрат") 78
6.3. Показательный (экспоненциальный) закон распределения 79
6.3.1 Числовые характеристики показательного распределения 80
6.3.2. Функция надежности 82
6.4. Распределение Парето 83
Глава 7. Закон больших чисел 84
7.1. Неравенство Чебышева 85
7.2. Теорема Чебышева 86
7.3. Обобщенная теорема Чебышева 87
7.4. Теорема Маркова 89
7.5. Теорема Бернулли 89
7.6. Центральная предельная теорема 90
Раздел 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 92
Глава 8. Основные понятия и задачи математической статистики 92
8.1. Выборочные распределения 94
8.1.1. Группирование данных, гистограмма, полигон 95
8.2. Статистическая (эмпирическая) функция распределения 98
8.3. Выборочные значения и оценка параметров. 100
8.3.1. Требования "хороших оценок" 101
Глава 9. Интервальное оценивание 103
9.1. Интервальная оценка математического ожидания при известной дисперсии 104
9.2 Интервальная оценка математического ожидания при неизвестной дисперсии 106
9.3. Интервальная оценка выборочной дисперсии 107
Глава 10. Статистические критерии 110
10.1. Проверка гипотез 111
10.2. Ошибки проверки гипотез 113
Раздел 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ 115
Глава 11. Основные понятия и модели случайных процессов 115
11.1. Классификация случайных процессов 116
11.2. Основные характеристики случайного процесса 117
11.2. Стационарные случайные процессы 121
11.3. Марковские случайные процессы 122
11.4. Потоки событий (Пуассоновские потоки) 125
11.5. Непрерывный марковский процесс. Уравнения Колмогорова 128
ЗАКЛЮЧЕНИЕ 131
Список литературы 131