7.7.2.Характеристики невизначеності

На практиці, при обчисленнях без використання спеціальних програм, використовують статистичні дані крапкових (точечних) значень імовірностей, упускаючи дані про тип розподілу імовір­ностей вихідних даних і їхніх невизначеностей.

Розглянемо значення знання чинників, які характеризують точність статистичних даних. На рис.7.6. представлені криві розподілу щільності імовірності нормального розподілу випад­кових величини з одним і тим же математичним очікуванням, але різними дисперсіями, причому значення математичного очі­кування (І = 0,0002 — типове значення величини випадкового небезпечного чинника. Значення дисперсії обрані а₁ = 0,00005 — малі значення невизначеності, а₂ = 0,0001 досить добрі зна­чення, а₃ = 0,0003 звичайні, що часто зустрічаються у варіантах представлення даних випадкової величини.

Як бачимо, випадкові величини з більшою дисперсією як би більш розмиті біля середніх значень, діапазон значень їхньої області існування більш широкий, максимальні і мінімальні зна­чення більш віддалені одне від одного. Зазначимо, що геометрично стандартні відхилення а збігаються з відстанню від серед­нього значення й до точок перегину кривої. Для випадкової величини в з нормальним розподілом імовірності спостережен­ня її значень в інтервалах ц ± а; (І ± 2а; (І ± За; рівні відповідно: 0,683,0,955, 0,997.

Для наведеного прикладу і довірчої імовірності Р ~ 95% (діа­пазон |я ± 2а) відповідні довірчі інтервали будуть:

(0,0001; 0,0003) для 0! = 0,00005, (перевага)

(0; 0,0004) для ст₂ = 0,0001, (-0,0004; 0,0008) для а₃ = 0,0003.

Іншими словами, з імовірністю 95%, випадкова величина в буде знаходитися в цих інтервалах. Зазначимо, що в останньому ви­падку, при а₃ = 0,0003, ширина довірчого інтервалу перевищує середнє значення випадкової величини в 6 (шість) разів, тобто дані з меншими невизначеностями мають більшу перевагу, вищість. Крім того нижня межа останнього інтервалу виходить за межі допустимих значень — прийме від'ємне значення, на практиці це означає що інтервал імовірного значення змінної розширюється від нуля до чотирьохкратного значення.

Нормальний розподіл грає дуже важливу роль у математичній статистиці. Воно описує випадкові величини, що мають лише загальні властивості: безперервність значень, рівноймовірність симетричних відносно (Я відхилень, більша імовірність малих відхилень від (я.

Нормальний розподіл з математичним очікуванням |я і дис­персією а² описується такою формулою для імовірності Р(у) ви­падкової величини у.

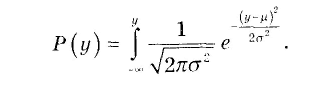
Визначення меж зон умов безпечної експлуатації АЕС.

Властивість групування випадкових величин в околиці їхніх математичних очікувань покладено в основу визначення зон припустимої і неприпустимої експлуатації для всіх параметрів безпеки АЕС. При цьому попередньо обробляються результати експлуатації за останні 5 років по всіх атомних станціях. Якщо відхилення параметра від середніх значень в умовах даної АЕС має випадкове походження, статистичні характеристики парамет­ра практично не змінюються, у випадку стабільних відхилень, робиться висновок про наявність причин відхилень параметра і проводиться їхнє визначення і пошук по спеціальних алгорит мах. Межі зон умов безпечної експлуатації АЕС — ілюстрація застосування принципу закономірності випадкових величин у практичній діяльності по забезпеченню безпечних умов життєд­іяльності суспільства.

Зелена зона (зона нормальної експлуатації) — визначається як така, у якій знаходяться 68% значень параметра (показника), тобто з 16% по 84%>, що відповідає інтервалу [|я - а; ц + а; ] для нормального симетричного розподілу (див. рис.7.8);

Біла зона (припустима)- визначається як область, в яку попа­дають до 26% значень показника, з 3% по 16%> і з 84% по 97%, що, приблизно, відповідає двом інтервалам: (|я - 2о~; [І - а) й (|а і а; ц + 2а;) для нормального симетричного розподілу;

Жовта зона (зона втручання органів регулювання безпеки) — визначається як область, у яку попадають до 4% значень по­казника, з 1% до 3% і з 97% по 99% що, приблизно, відповідає двом інтервалам: (ц — За; (я - 2а) і (й, +2а; (я -1- Зо;) для нормаль­ного симетричного розподілу;

Червона зона (неприпустима) — визначається як область, у кот­ру попадають значення показника менш 2 % усіх його значень, що, приблизно, відповідає інтервалам: [0,(|и - За);] і [(й + За), °°] для нормального симетричного розподілу.

На рис.7.7 прийняті такі позначення: ц — математичне очі­кування, а — стандартне відхилення, тіп, тах — мінімальне і максимальне значення показника, Г(л:) — поточне значення по­хідної ^N/^X змінної величини X (показника).

Зазначимо, що сучасні програми обробки даних підтримують біля двох десятків типів розподілу випадкових величин, наприк­лад: логнормальне, Пуассона, експонентне, Хі-квадрат, Ст^гьюден-та, рівномірне, гама розподіл і т. інш. [9, 41].

При порівнянні випадкових величин, що мають навіть одна­кові типи розподілу імовірностей, обов'язково необхідно вказу­вати значення дисперсії чи параметра, що характеризує розсіян­ня випадкової величини біля її середніх значень.

Можливий варіант, коли при рівних, чи навіть великих зна­ченнях середніх (Імовірностей), але значних дисперсіях, значен­ня довірчих інтервалів істотно відрізняються і твердження про рівність чи великі значення гшзикіб будуть неправомірними.

На підставі вищесказаного можна зробити висновок: порівнян­ня ризиків, у розумінні порівняння випадкових величин, необхі­дно робити з урахуванням невизначеностей.