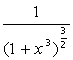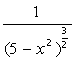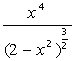Порядок выполнения задания

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите подынтегральную функцию как функцию переменной х и постройте ее график.

3. Вычислите определенный интеграл.

4. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в левом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

5. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в правом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

6. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в середине отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

7. Сравните полученные значения пределов между собой и со значением интеграла.

8. Постройте графики интегральных сумм как функций числа разбиений отрезка интегрирования.

9. Постройте графики интегральных сумм как функций длины отрезка разбиений.

Выполните индивидуальные задания, приведенные ниже, подготовьте ответы на контрольные вопросы.

Индивидуальные задания к лабораторной работе 5.

1. Найдите производную функции f(x) тремя способами:

• по определению;

• аналитически, используя строку меню;

• аналитически, используя панель инструментов.

Вычислите значение производной в точке x=0, имея в виду, что f(0)=0.

	f(x)		f(x)
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

2. Вычислите неопределенный интеграл  и проверьте правильность вычислений, постройте графики семейства первообразных.

	f(x)		f(x)
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

3. Вычислить неопределенный интеграл заменой переменных

	f(x)		f(x)
1		12
2			Применяя тригонометрические подстановки , , и т.п.
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20	Применяя подстановку :
11

4. Вычислить значение интеграла от линейной функции , построить график подинтегральной функции, определить площадь соответствующей фигуры, записать выражения для интегральных сумм (при разбиении отрезка интегрирования на N равных частей), найти пределы интегральных сумм и построить графики зависимости интегральных сумм от N и от D.

	f(x)	[a, b]			f(x)	[a, b]
1		[0, 16]		11		[0,4 ]
2		[0, 1]		12		[0,2 ]
3		[0, 5]		13		[0, ]
4		[3, 5]		14		[6, 9]
5		[0, ]		15		[8, 12]
6		[0, ]		16		[6, 10]
7		[0, 4]		17		[0, 3]
8		[0, 2]		18		[1, 64]
9		[0, 4]		19		[0, 3]
10		[0, 5]		20		[0, 1]