Робота 8. Дослідження роботи лінійної системи автоматичного керування при випадкових впливах

8.1. Мета роботи

Ознайомитися з аналізом поведінки системи автоматичного керування при випадкових впливах, експериментально дослідити вплив завад на точність роботи лінійної системи автоматичного регулювання

8.2. Теоретичні відомості

На практиці більшість систем автоматичного керування працює в умовах постійно діючих випадкових, корисних і шкідливих впливів. Корисним є, наприклад, такий вплив як вхідний (задаючий) сигнал слідкуючої системи. До шкідливих випадкових впливів відносяться різні внутрішні і зовнішні завади, зміни напруги мережі тощо. Корисні випадкові (і невипадкові) впливи система керування повинна відтворити або перетворити за заданим законом найбільш точно. Система керування будується таким чином, щоб шкідливі випадкові впливи вносили мінімальну помилку в закон перетворення корисного сигналу.

Для аналізу поведінки системи при випадкових впливах, зокрема при виборі її параметрів, які забезпечують найбільшу точність роботи, необхідно використовувати математичний апарат теорії випадкових процесів.

Випадковий процес характеризується випадковою функцією, яка є функцією часу , значення якої в кожний конкретний момент часу t є випадковою величиною. В результаті проведення експерименту випадкова функція реалізується у вигляді будь-якої конкретної функції, яка називається реалізацією. Нескінчена множина можливих реалізацій узагальнюється поняттям випадкової функції. Ордината випадкової функції в кожний заданий момент часу - випадкова величина. Таким чином, випадкова функція представляє собою сукупність нескінченої множини випадкових величин, тому дати повну ймовірнісну характеристику у вигляді закону розподілення неможливо. В практичних задачах звичайно обмежуються неповною характеристикою випадкової функції, використовуючи такі поняття, як: математичне очікування, дисперсія, кореляційна функція.

Математичним очікуванням випадкової функції X(t) називається така невипадкова функція m_x(t), значення якої при кожному даному значенні аргументу t дорівнює математичному очікуванню випадкової функції X(t) при цьому значенні t:

m_x(t) = M[X(t)]. /8.1/

Математичне очікування випадкової функції характеризує її середнє значення. Різниця між випадковою функцією і її математичним очікуванням - відхилення випадкової функції від її математичного очікування, називається центрованою випадковою функцією

. /8.2/

Дисперсією випадкової функції X(t) називається математичне очікування квадрата центрованої випадкової функції:

. /8.3/

Дисперсія випадкової функції характеризує розкид можливих реалізацій відносно математичного очікування. Вона визначає ширину смуги, заповненої можливими реалізаціями випадкової функції. Середнє квадратичне відхилення випадкової функції

. /8.4/

Кореляційна функція випадкової функції X(t) є невипадкова функція двох аргументів , яка при кожній парі значень t і дорівнює кореляційному моменту відповідних перерізів випадкової функції:

. /8.5/

За умови, що , маємо

, /8.6/

тобто в цьому випадку кореляційна функція згортається в дисперсію випадкової функції. Вона характеризує ступінь залежності між двома перерізами випадкової функції.

Для визначення залежності між двома випадковими функціями X(t) і Y(t) призначена взаємна кореляційна функція:

. /8.7/

Випадкові функції, для яких математичне очікування і дисперсія сталі, а кореляційна функція залежить тільки від інтервалу часу , називаються стаціонарними. Отже, для стаціонарної випадкової функції:

m_x(t) = m_x = const;

D_x(t) = D_x = const;

.

Оскільки , то для стаціонарної випадкової функції

. /8.8/

Вимога незмінності значення математичного очікування для стаціонарної випадкової функції несуттєва, так як останню завжди можна центрувати і отримати випадкову функцію з m_x = 0 = const. Таким чином, єдиною умовою стаціонарності є

. /8.9/

Існують випадкові процеси, для яких справедлива ергодична теорема: будь-яка статична характеристика, яка отримана усередненням за множиною з ймовірністю, наближеною до одиниці, співпадає з характеристикою, яка отримана усередненням за часом. Інколи дане положення вважають очевидним, навіть якщо воно не доведено. Тоді говорять про ергодичну гіпотезу, яка застосовується для багатьох стаціонарних процесів. На практиці ергодична гіпотеза дозволяє отримати характеристики випадкового процесу всього лише при одній реалізації достатньої тривалості.

Для ергодичних випадкових процесів математичне очікування m_x, кореляційна функція і дисперсія D_x визначають за виразами:

; /8.10/

; /8.11/

. /8.12/

Для стаціонарних випадкових функцій вводиться ще одне поняття - спектральна густина, яка характеризує розподілення середнього значення потужності процесу по спектру функції. Спектральна густина є зображенням Фур’є від кореляційної функції:

. /8.13/

Відповідно обернене перетворення Фур’є дає можливість знайти кореляційну функцію за спектральною густиною:

. /8.14/

Дисперсія випадкової функції пов’язана зі спектральною густиною виразом:

. /8.15/

Для двох випадкових процесів X(t) і Y(t), як і для кореляційних функцій, вводиться поняття взаємної спектральної густини:

;

.

Розглянемо перетворення стаціонарного випадкового сигналу лінійною динамічною системою. Нехай на лінійну систему, яка має передаточну функцію W(s), діє стаціонарний випадковий сигнал X(t) з математичним очікуванням m_x(t) і кореляційною функцією . На виході системи сигнал Y(t) буде також випадковим з математичним очікуванням m_y(t) і кореляційною функцією в усталеному режимі . Оскільки m_x(t) - невипадкова функція часу, то m_y(t) знаходимо звичайним для невипадкових сигналів способом:

,

де

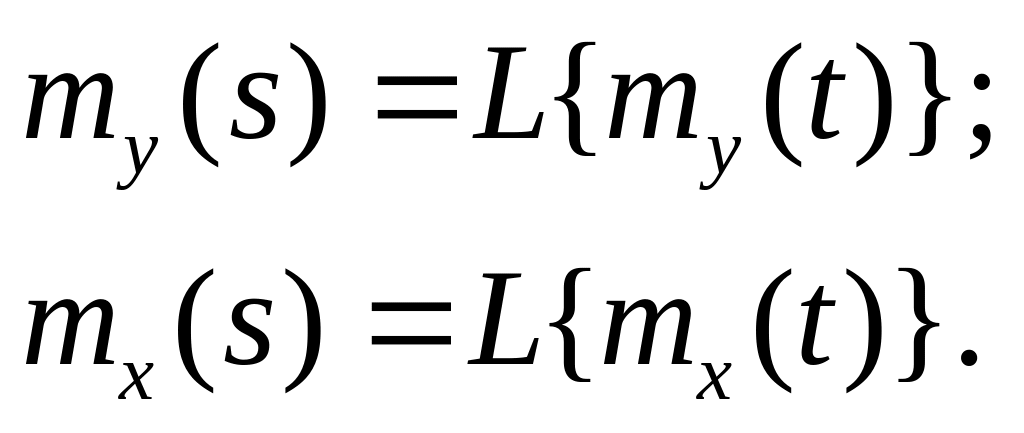
Визначимо кореляційну функцію стаціонарного випадкового сигналу на виході системи:

. /8.16/

На підставі рівняння згортки маємо

; /8.17/

, /8.18/

де - вагова функція системи.

Визначимо стаціонарний сигнал на виході, який встановлюється при . Змінивши верхні межі інтегрування в /8.17/ і /8.18/ на і підставивши в /8.16/, отримаємо

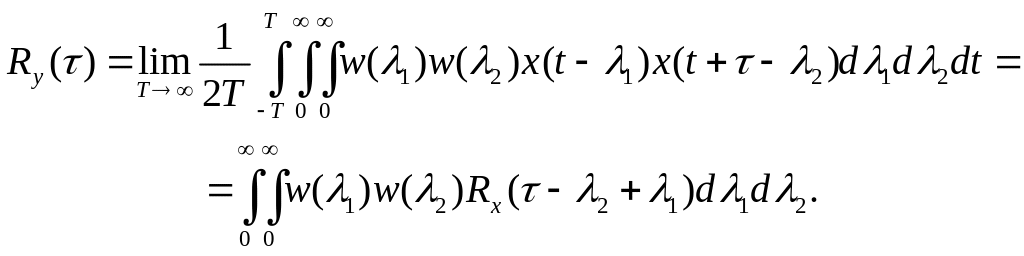/8.19/

З рівняння /8.19/ можна знайти кореляційну функцію випадкового сигналу на виході за відомою кореляційною функцією вхідного сигналу.

Визначимо закон перетворення спектральної густини. Нехай кореляційній функції відповідає спектральна густина . Тоді для спектральної густини вихідного сигналу маємо

. /8.20/

Підставляємо вираз для з /8.19/ в /8.20/ і отримаємо

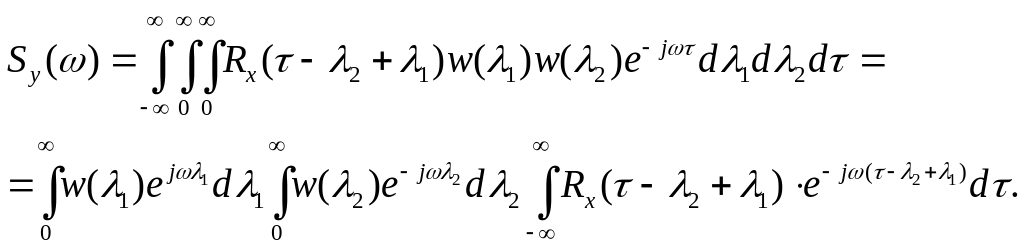
Оскільки

,

то остаточно маємо

. /8.20/

Дисперсія сигналу на виході

. /8.21/

При обчисленні інтегралу /8.21/ підінтегральний вираз записується у вигляді:

,

де

,

.

В загальному випадку при будь-якому n для стійкої системи інтеграл

може бути представлений у вигляді

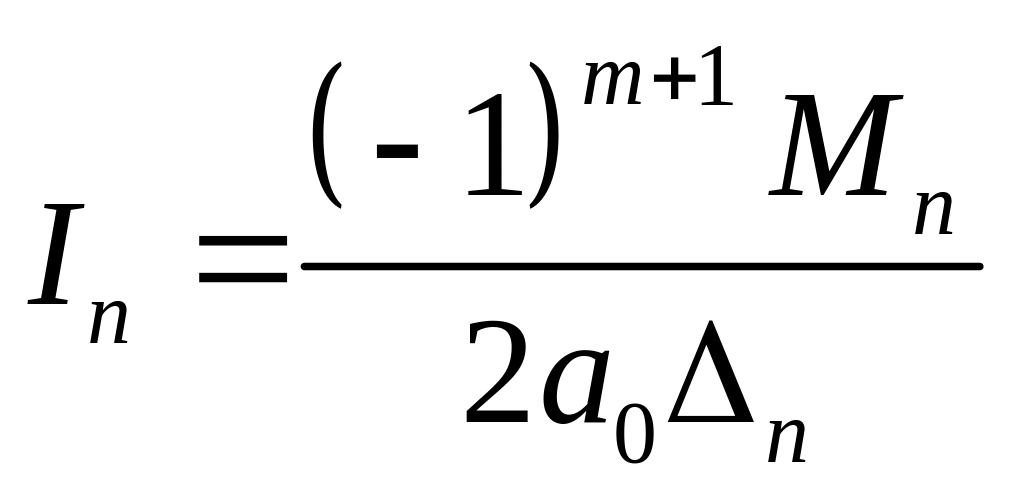, /8.22/

де

;

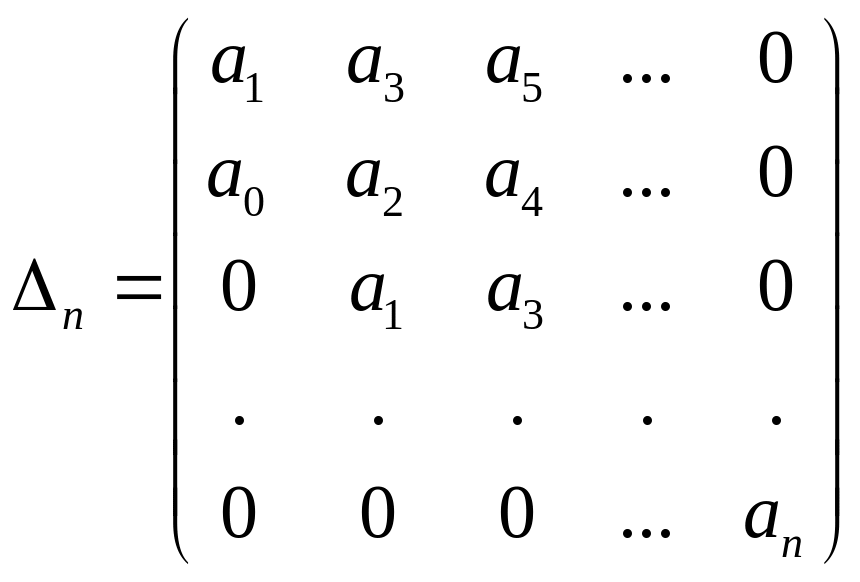Розглянемо спочатку загальний випадок САК, на яку діє одночасно корисний стаціонарний випадковий сигнал g(t) і стаціонарна завада N(t) (рис.8.1).

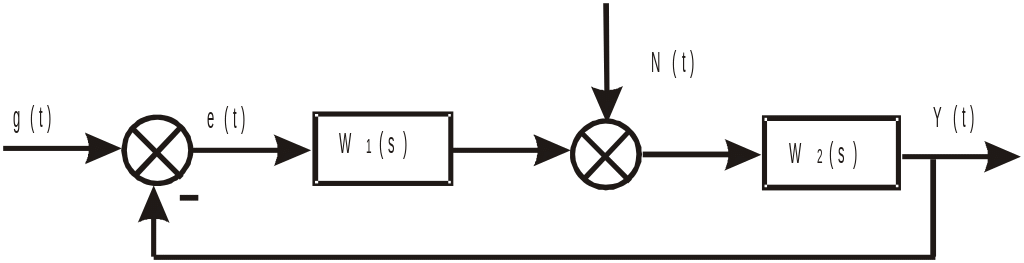
Рис.8.1. Структурна схема системи з завадою.

Знайдемо дисперсію похибки відтворення корисного сигналу g(t) в усталеному режимі (D_е).

Похибкою системи e(t) вважають різницю між дійсною вихідною величиною y(t) і бажаною (ідеальною), за яку, за звичай, приймають вхідну величину g(t). Чим точніше відпрацьовується системою вхідна величина, тим якісніша система і менше її похибка:

e(t) = g(t) - y(t).

Оскільки система лінійна, то похибка e(t) визначається двома складовими, обумовленими дією сигналів g(t) і N(t):

.

Дисперсія похибки

,

де - дисперсія складової похибки від корисного сигналу; - дисперсія складової похибки від сигналу завади; - взаємний кореляційний момент e_g(t) і e_N(g).

Вважаючи g(t) і N(t) некорельованими, отримаємо

. /8.23/

Згідно /8.21/ для складових дисперсії маємо

; /8.24/

, /8.25/

де - передаточна функція похибки від корисного сигналу g(t); - передаточна функція похибки від завади N(t).

При відомих параметрах об’єкта, використовуючи формулу /8.23/, можна обчислити D_e.

В даній лабораторній роботі необхідно визначити оптимальне значення одного з параметрів системи - сталої часу Т_и інтегруючого елемента моделі об’єкта керування, при якій забезпечується мінімум дисперсії похибки. Для цього за формулою /8.23/ обчислюється D_e = f(T_и). Оптимальне значення Т_и знаходимо звичайним способом з виразу

.

Отримаємо вираз для дисперсії похибки системи, досліджуваної в даній лабораторній роботі. Структурна схема досліджуваної системи наведена на рис.8.2.

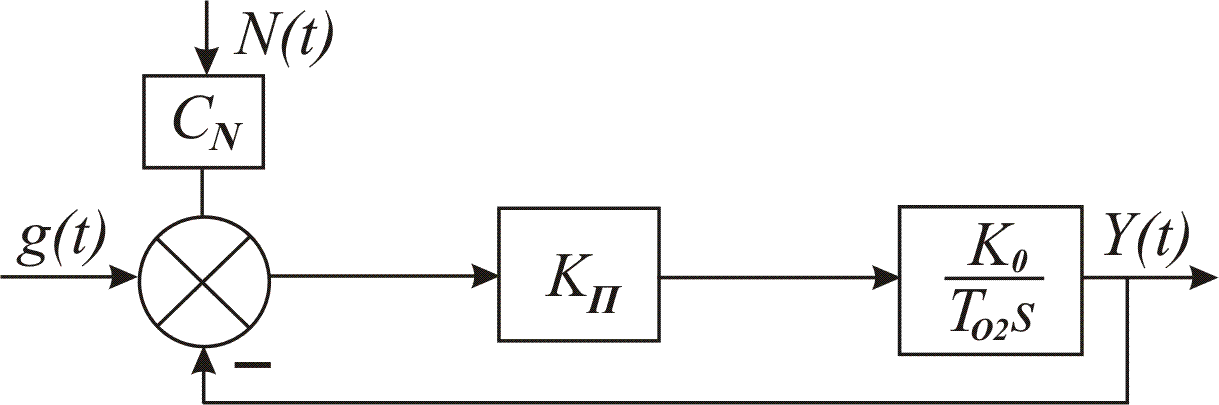
Рис.8.2. Структурна схема досліджуваної САК із завадою на вході.

Передаточна функція похибки від корисного сигналу

,

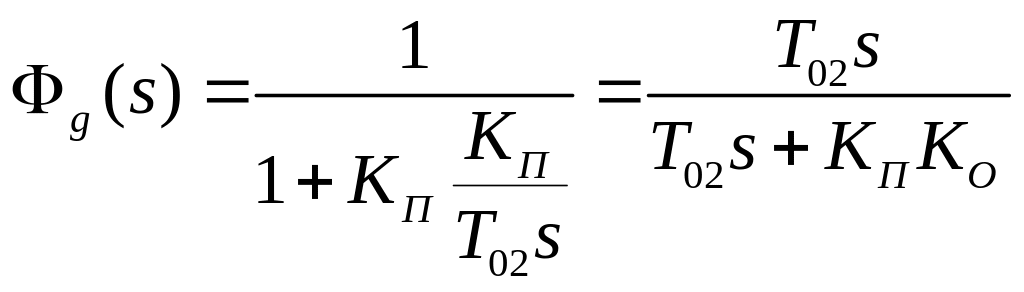де – коефіцієнт передачі регулятора; – коефіцієнт передачі об’єкта; шуканий параметр Т_и = Т₀₂.

Передаточна функція похибки від завади

.

Нехай корисний сигнал являє собою синусоїдний сигнал з випадковою фазою

,

у якого фаза розподілена за рівномірним законом

.

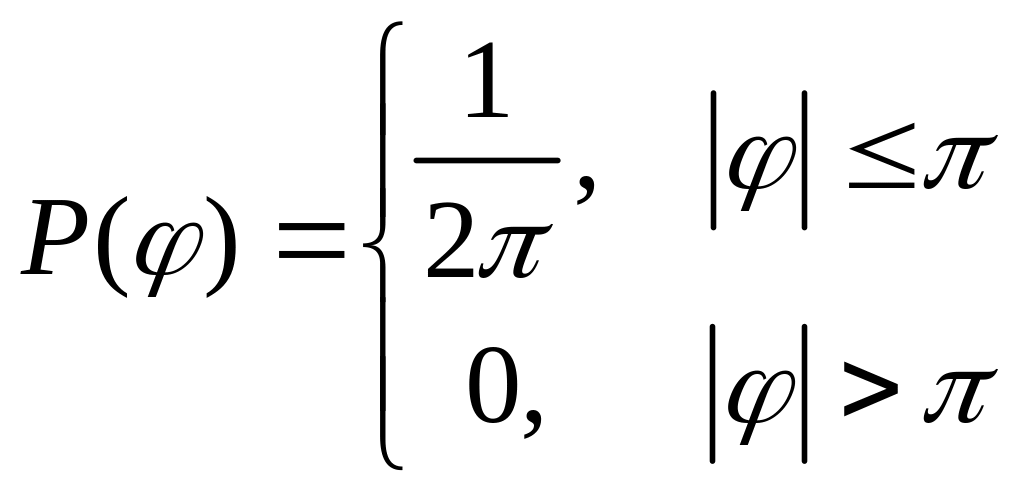Складова похибки від корисного сигналу може бути обчислена за формулою /8.24/. Спектральна густина синусоїдного сигналу являє собою суму двох - функцій, розташованих на частотах і :

. /8.26/

Після підстановки /8.26/ у вираз /8.24/, отримаємо

.

На основі фільтруючої властивості - функції

отримаємо

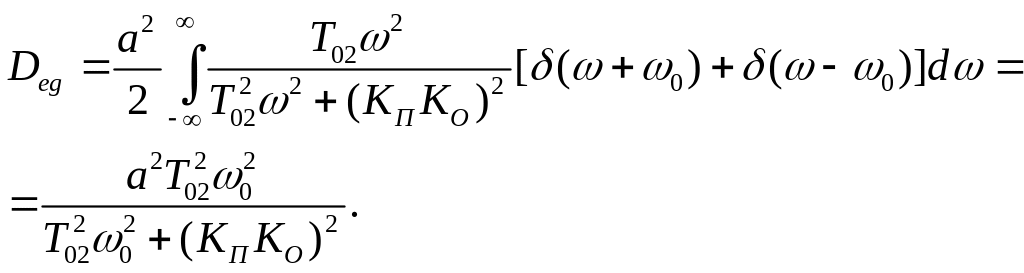
Розрахуємо складову дисперсії похибки D_eN від завади N(t).

Графік спектральної густини завади наведений на рис.8.3.

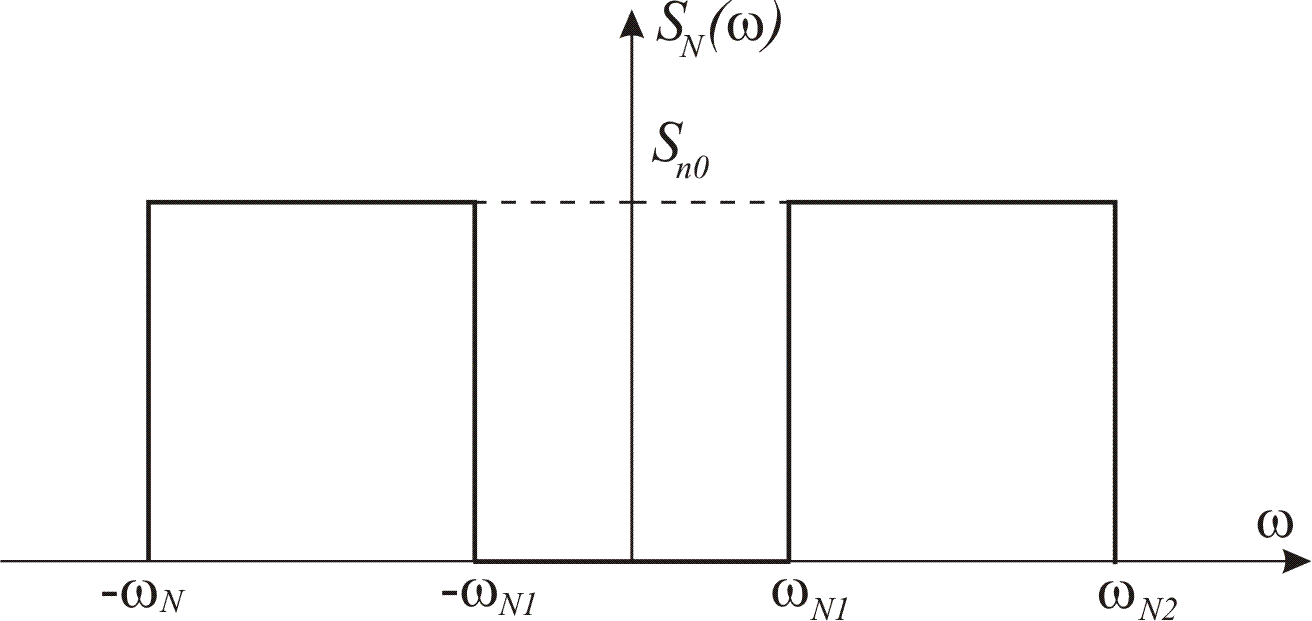
Рис.8.3. Спектр завади.

Математичне очікування завади дорівнює нулю, бо вона симетрична відносно осі . Величина S_N0 визначається з виразу

.

Звідси

.

Верхня і нижня частоти спектра завади і середньоквадратичне значення задані.

Дисперсія похибки від завади згідно /8.25/

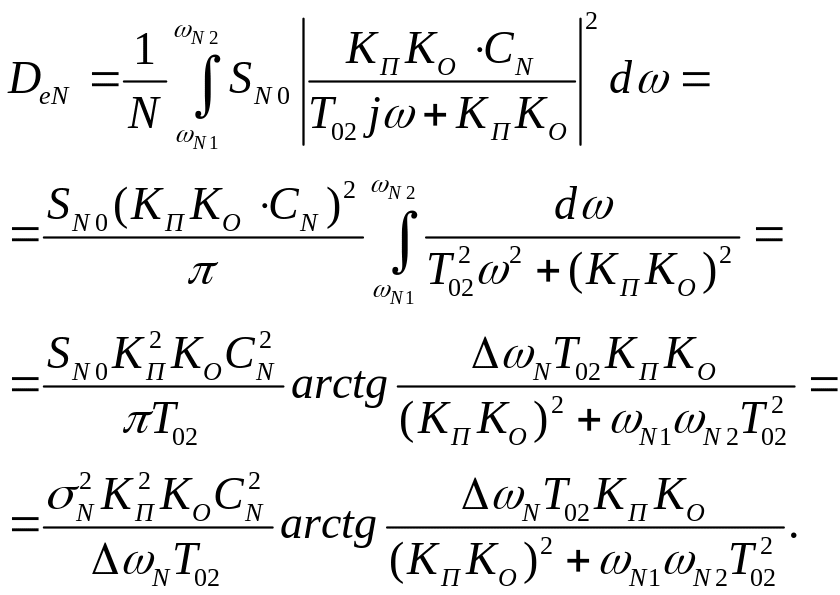
Сумарна дисперсія похибки

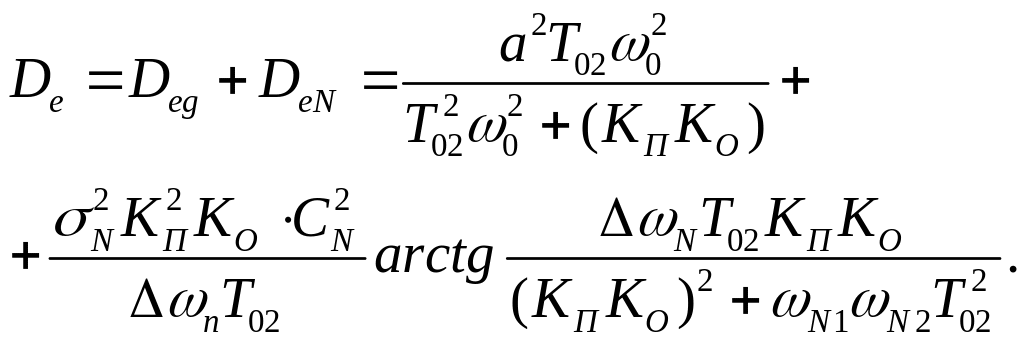/8.27/

Вираз /8.27/ дозволяє побудувати графік залежності дисперсії похибки від сталої часу Т₀₂. Якісно цей графік наведений на рис.8.4.

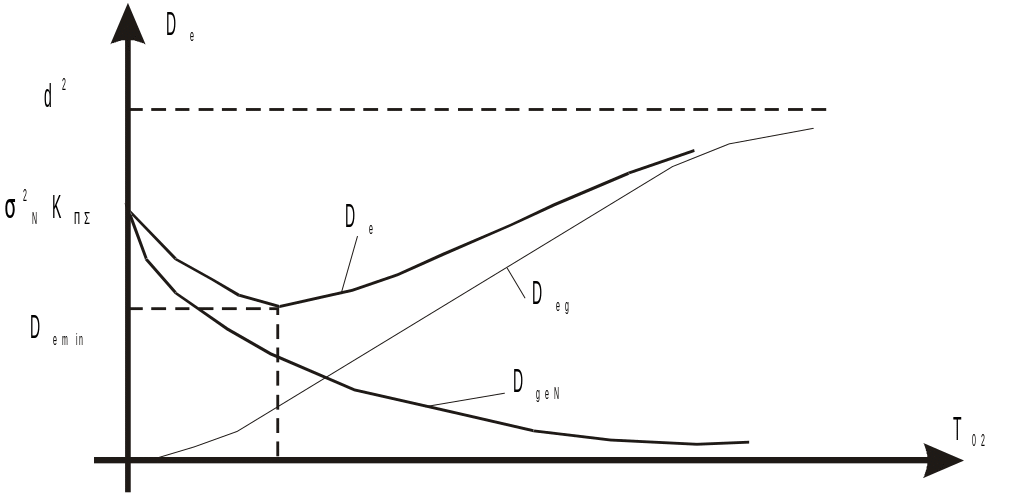
Рис.8.4. Графік залежності дисперсії помилки корисного сигналу

від зміни постійної часу Т₀₂.

Як видно з графіка, функція D_e(T₀₂) має мінімум. Визначення оптимального значення сталої часу T_02опт і є кінцевою метою досліду в даній лабораторній роботі.

Розглянемо спосіб експериментального визначення дисперсії похибки, який реалізовано в даній лабораторній роботі. Сигнал похибки e(t) пропускається через квадратор, на виході якого отримаємо випадковий сигнал e²(t). Потім цей сигнал поступає на аперіодичну ланку з сталою часу . Сигнал на виході аперіодичної ланки записується у вигляді:

,

де - вагова функція аперіодичної ланки.

Визначимо границю f(e) при

.

Прийнявши верхню межу, рівною , і перепозначивши змінну інтегрування, отримаємо

.

Отже, якщо стала часу аперіодичної ланки , то на її виході отримаємо значення дисперсії похибки D_e. Тут відіграє роль часу спостереження. Але, так як час спостереження і стала часу реально не можуть бути нескінченними, то фактично на виході аперіодичної ланки ми отримаємо оцінку дисперсії

.

Якщо вибрати час спостереження - сталу часу , за умови

,

де - нижча частота спектра випадкового сигналу e²(t), то точність обчислення дисперсії складе приблизно 2%, що є задовільним. За нижчу частоту спектра можна прийняти частоту корисного сигналу . Тоді необхідна стала часу аперіодичної ланки , що і реалізовано в лабораторному стенді.