Робота 6. Дослідження впливу постійного запізнення на стійкість лінійної системи
6.1. Мета роботи
Ознайомитися з методами аналізу стійкості систем автоматичного регулювання при наявності постійного запізнення, дослідити вплив величини запізнення на запаси стійкості лінійної системи.
6.2. Теоретичні відомості
В ланках із постійним запізненням вхідна величина без змін передається на вихід ланки, але із запізненням на проміжок часу з моменту появи сигналу на вході ланки:
.
/6.1/
В операторній формі запису із використанням теореми запізнення рівняння /6.1/ приймає вигляд
.
/6.2/
На основі /6.2/ легко отримати передаточну функцію ланки з постійним запізненням
.
/6.3/
Після
підстановки
отримується вираз для амплітудно-фазової
частотної характеристики ланки із
постійним запізненням
.
/6.4/
При цьому очевидно, що амплітудно-частотна характеристика ланки із постійним запізненням рівна одиниці:
.
/6.5/
Фазова частотна характеристика ланки із постійним запізненням
.
/6.6/
З виразу /6.6/ видно, що зі збільшенням частоти сигналу різниця фаз між вихідною і вхідною величиною лінійно зростає.
До складу систем автоматичного регулювання ланка із постійним запізненням може входити послідовно з іншими ланками, або бути ввімкнутою в коло зворотного зв’язку.
На
рис.6.1 наведена структурна схема системи
автоматичного регулювання з постійним
запізненням, зведена до найпростішої.
Зі схеми видно, що ланка із постійним
запізненням ввімкнена послідовно з
іншими ланками системи, які об’єднані
в одну ланку з еквівалентною передаточною
функцією
.
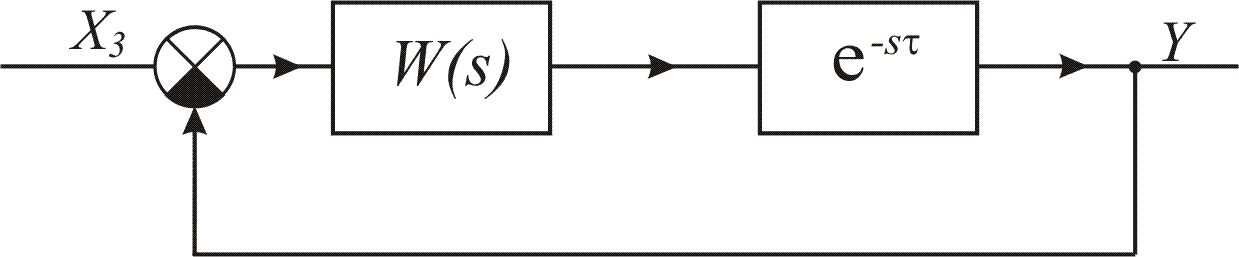
Рис.6.1. Структурна схема системи автоматичного
регулювання зі сталим запізненням.
Якщо в системі є кілька ланок із запізненням, то їх також можна замінити однією ланкою із сумарним запізненням.
Запишемо вираз для передаточної функції розімкненої системи автоматичного регулювання з постійним запізненням (рис.6.1):
.
/6.7/
Передаточна функція замкнутої системи для цього випадку приймає вигляд
.
/6.8/
Згідно з виразом /6.8/ характеристичне рівняння замкнутої системи має вигляд
/6.9/
Це рівняння є трансцендентним і має нескінченну кількість коренів. Аналіз стійкості за коренями у цьому випадку є трудомістким і тому використовуються частотні критерії стійкості, зокрема, критерій стійкості Найквіста.
Амплітудно-фазову частотну характеристику розімкненої системи отримаємо з передаточної функції шляхом заміни
.
/6.10/
Якщо
в /6.10/ покласти
,
то отримаємо амплітудно-фазову частотну
характеристику, так званої, граничної
системи, яка матиме наступний вигляд:
.
/6.11/
Отже, під граничною розімкненою системою розуміють таку систему, в якій запізнення зменшується до нуля, а ланка із постійним запізненням перетворюється у безінерційну ланку з коефіцієнтом передачі рівним одиниці.
Порівняння
виразів /6.10/
і /6.11/
показує, що для побудови годографа
системи із постійним запізненням
необхідно кожен радіус-вектор
характеристики граничної системи
додатково повернути за годинниковою
стрілкою на кут величиною
,
як показано на рис. 6.2. Це призводить до
того, що годограф амплітудно-фазової
частотної характеристики розширюється
відносно годографа системи без запізнення
і наближається до критичної точки
.
При цьому запас стійкості по фазі системи
із запізненням зменшується на величину
.
Із наведених годографів можна визначити
зміну запасу стійкості і по амплітуді,
провівши з точки
кола дотичні до годографів
і
.
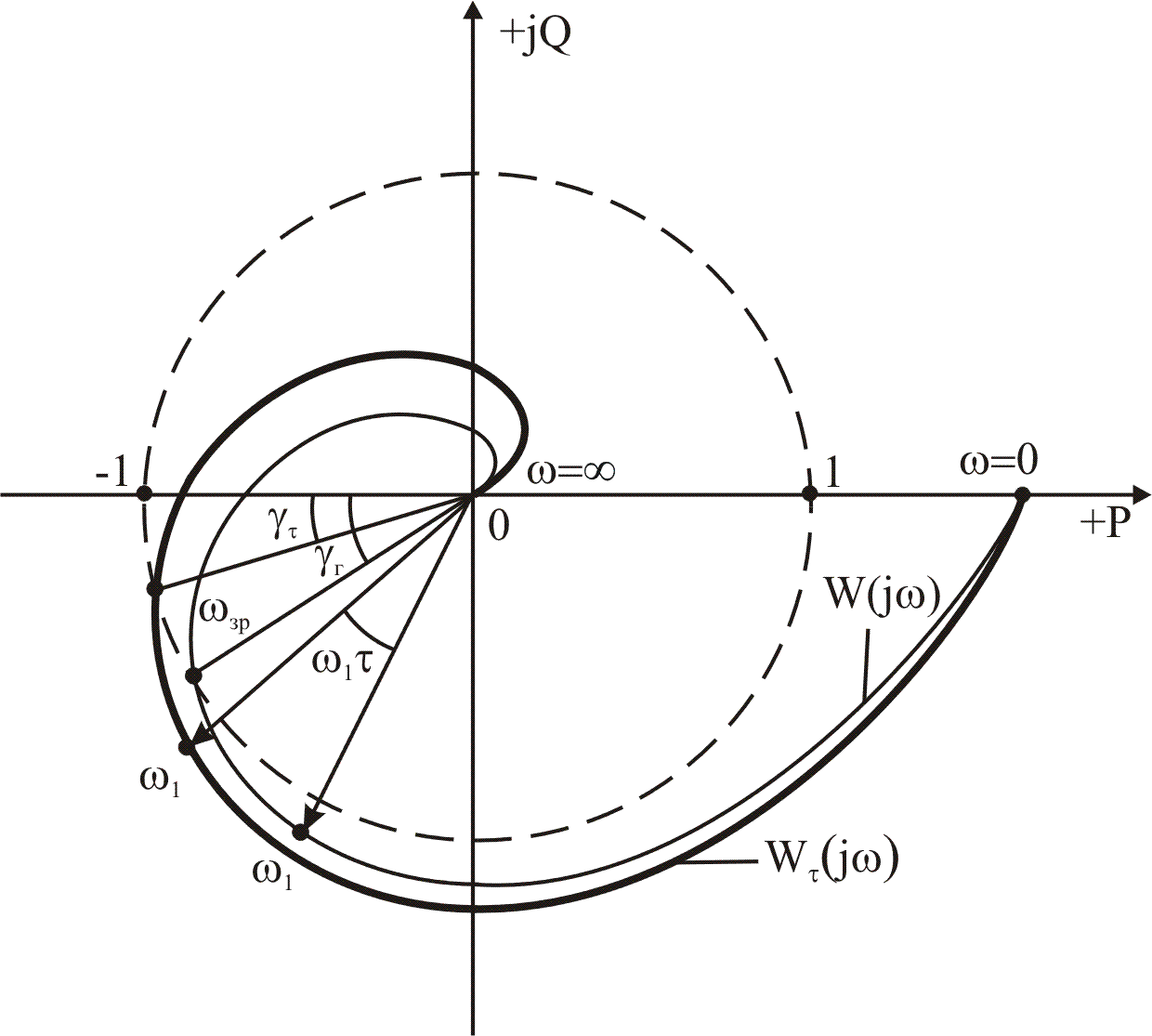
Рис.6.2. Побудова годографа амплітудно-фазової
характеристики системи з постійним запізненням.
Знаючи
запас стійкості граничної системи за
фазою
легко розрахувати критичне значення
запізнення
,
при якому система буде знаходитись на
межі стійкості
,
/6.12/
де
–
частота зрізу.
На практиці, для визначення запасів стійкості широко використовуються логарифмічні частотні характеристики. Методику визначення запасів стійкості за цими характеристиками показано на рисунку 6.3.
Рис. 6.3. Визначення запасів стійкості за логарифмічними частотними характеристиками.
Часто для спрощення аналізу динамічні властивості ланок з високим порядком представляють ланкою низького порядку, але із фіктивним запізненням.