Робота 5. Дослідження стійкості лінійних систем

автоматичного регулювання

5.1 Мета роботи

Ознайомитися з методами аналізу стійкості лінійних систем автоматичного регулювання з типовими регуляторами, експериментально дослідити вплив настроювальних параметрів регуляторів на стійкість системи та навчитися визначати критичні значення параметрів.

5.2. Загальні відомості

Під стійкістю систем автоматичного керування розуміють їх здатність повертатися до вихідного усталеного режиму після короткочасної дії керуючої чи збурюючої величини, яка виводить систему з початкової рівноваги.

Динамічні властивості безперервних лінійних систем з зосередженими параметрами описуються неоднорідними диференціальними рівняннями з постійними коефіцієнтами. Ці рівняння прийнято записувати у вигляді

, /5.1/

де регульована величина, вхідна дія.

Ліва частина диференціального рівняння /5.1/

/5.2/

описує вільний рух системи.

Цей рух стійкий, якщо

, /5.3/

де - загальний розв'язок однорідного диференціального рівняння.

Загальний розв’язок однорідного диференціального рівняння /5.2/ складається із суми експонент

, /5.5/

де - сталі інтегрування, - корені характеристичного рівняння системи.

Характеристичне рівняння можна утворити із диференціального рівняння системи.У цьому випадку характеристичне рівняння є рівнянням для полюсів передаточної функції і може бути отримане з передаточної функції замкненої системи, якщо знаменник передаточної функції прирівняти до нуля. Для диференціального рівняння /5.1/ характеристичне рівняння має вигляд

. /5.6/

Корені характеристичного рівняння можуть бути дійсними або комплексними числами. Для довільної пари комплексно-спряжених коренів можна записати

, /5.7/

де і - відповідно дійсна і уявна частини -го кореня.

Границя суми прямує до нуля

, /5.8/

якщо з плином часу кожна її складова прямує до нуля

/5.9/

На основі теореми Ейлера умову /5.9/ у випадку комплексно-спряжених коренів можна привести до виду:

/5.10/

Щоб умова /5.10/ виконувалася, необхідно щоби було від’ємним числом.

Таким чином приходимо до формулювання основної умови стійкості: для стійкості лінійної системи необхідно і достатньо, щоб комплексні корені характеристичного рівняння мали від’ємні дійсні частини, або були від’ємними дійсними числами. Загальну умову стійкості можна сформулювати інакше: система є стійкою, якщо корені характеристичного рівняння лежать в лівій півплощині комплексної площини коренів (рис.5.1). Уявна вісь є межею, яка ділить комплексну площину коренів на дві області: ліву – стійку і праву - нестійку. Система знаходиться на границі стійкості, якщо один із коренів попадає на уявну вісь. При цьому в системі виникають автоколивання. В такому режимі лінійна система експлуатуватися не може.

Отже, для визначення стійкості систем автоматичного регулювання за загальною умовою стійкості необхідно знайти корені характеристичного рівняння і проаналізувати їх розташування на комплексній площині

а)

б)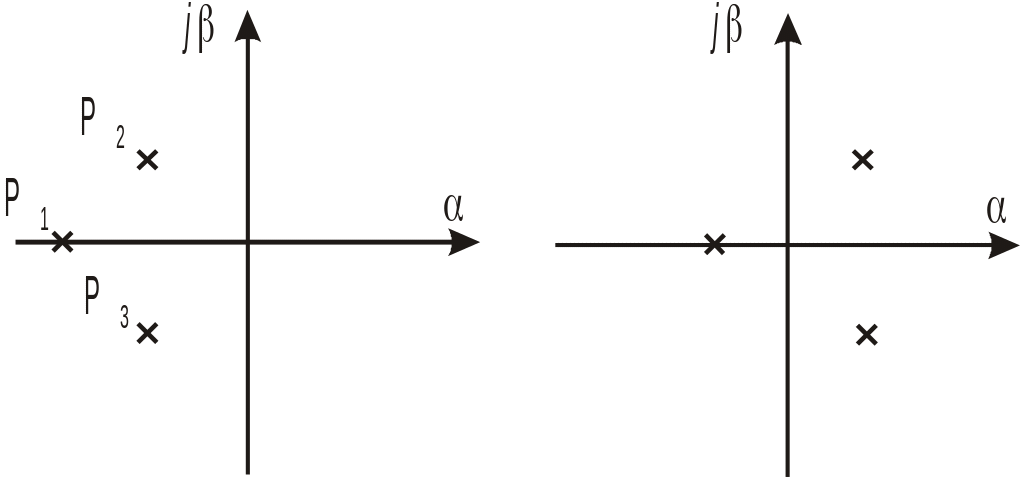

Рис.5.1.Аналіз стійкості за коренями характеристичного рівняння:

а) система стійка, б) система нестійка

Для знаходження коренів характеристичного рівняння 2-го і 3-го порядків можна скористатися відомими формулами, однак не існує загальних формул для визначення коренів рівнянь четвертого і вищого порядків. Тому були розроблені методи, що дозволяють досліджувати стійкість систем автоматичного керування без знаходження коренів характеристичного рівняння. Вони мають назву критеріїв стійкості. Критерії стійкості поділяються на алгебраїчні і частотні. До алгебраїчних належать критерії Рауса, Гурвіца, Льєнара-Шіпара, до частотних - критерії Михайлова та Найквіста.

Найчастіше для аналізу стійкості систем невисокого порядку ( ) та систем, до складу яких не входять ланки із постійним запізненням, використовують критерій Гурвіца, який приводить до тієї ж самої системи нерівностей, що і критерій Рауса. Тому, інколи, ці критерії називають критеріями Рауса-Гурвіца.

Для аналізу стійкості системи за критерієм Гурвіца складають визначник із коефіцієнтів характеристичного рівняння таким чином: по головній діагоналі розташовують коефіцієнти від до , далі місця в стовцях над діагоналлю заповнюють коефіцієнтами в порядку убування індексів, а знизу від діагоналі – у порядку зростання індексів. Пусті місця заповнюють нулями.

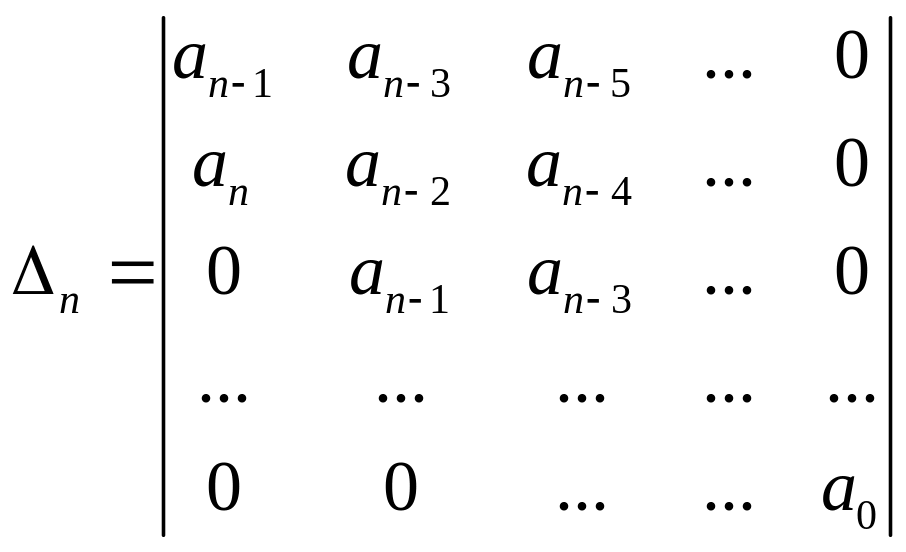
За критерієм Гурвіца замкнута система стійка, якщо при додатному знаку коефіцієнта , є також додатними, головний визначник Гурвіца і всі його діагональні мінори - , ,…, . Діагональні мінори утворюють з головного визначника шляхом відкреслювання відповідного числа рядків і стовпців.

Застосування критерію стійкості Гурвіца до систем першого і другого порядків показує, що вони є стійкими при скінчених додатних параметрах системи, однак системи третього і вищого порядків можуть втратити стійкість і при додатних значеннях параметрів.

Частотні критерії стійкості є досить зручними для аналізу стійкості систем високого порядку та систем із постійним запізненням.

При аналізі систем автоматичного керування важливо встановити вплив окремих параметрів системи на її стійкість та визначити область допустимих значень параметрів. Для цього можуть бути використані розглянуті вище критерії стійкості або загальні методи: метод кореневого годографа та метод D-розбиття. Для систем третього порядку область допустимих значень параметрів системи можна визначати за діаграмою Вишнеградського.

Зокрема, для знаходження критичного значення коефіцієнта передачі регулятора , при якому система буде знаходитись на границі області стійкості, можна скористатися критерієм стійкості визначника Гурвіца. Для цього необхідно прирівняти до нуля найстарший мінор визначника Гурвіца та розв’язати отримане рівняння відносно досліджуваного параметра. Для випадку системи третього порядку (п=3) з характеристичним рівнянням , і визначником Гурвіца

,

умова знаходження системи на межі стійкості приймає вигляд

. /5.11/

З цього рівняння визначають критичне значення будь-якого параметра, який входить в один із коефіцієнтів характеристичного рівняння.

Структурна схема системи автоматичного керування, що досліджується в даній роботі, може бути зведена до найпростішої (рис.5.2).

Рис.5.2 Структурна схема досліджуваної системи.

Динамічні властивості об’єкта керування в даній роботі описуються передаточною функцією

/5.12/

Передаточна функція керуючого пристрою для випадку

П-регулятора

. /5.13/

За цих умов передаточна функція розімкнутої системи

/5.14/

Знайдемо передаточну функцію замкнутої системи за формулою

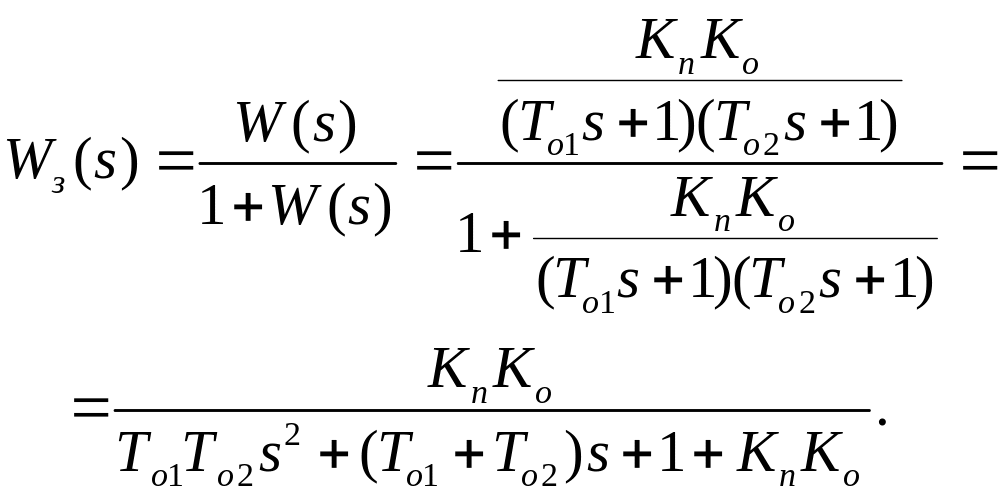/5.15/

З /5.15/ видно, що досліджувана система автоматичного керування з П-регулятором описується рівнянням другого порядку і згідно з критерієм стійкості Гурвіца не може втратити стійкості при додатних значеннях параметрів системи.

Знайдемо вираз для критичного значення коефіцієнта передачі системи у випадку використання І-регулятора.

Передаточна функція І-регулятора має вигляд

. /5.16/

Передаточна функція розімкненої системи

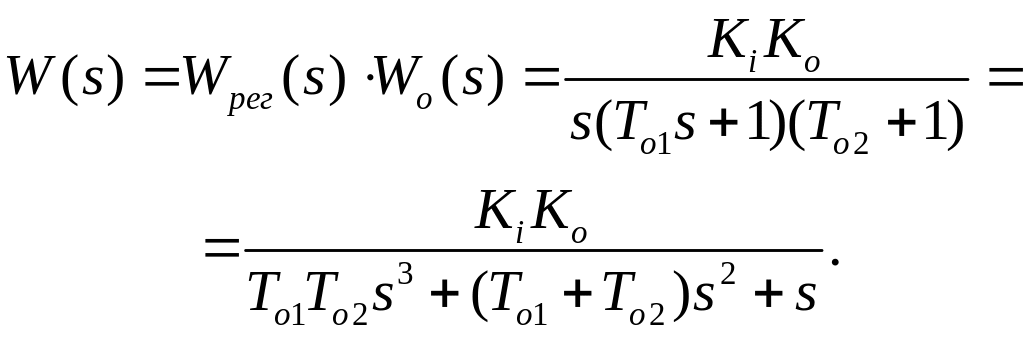/5.17/

Знайдемо вираз для передаточної функції замкнутої системи

/5.18/

На основі /5.18/ запишемо характеристичне рівняння досліджуваної системи автоматичного керування з І-регулятором

Для визначення критичного значення коефіцієнта передачі підставимо в рівняння /5.11/ ; ; ; і одержимо

. /5.19/

Розв’язок цього рівняння відносно дає вираз для знаходження критичного значення коефіцієнта передачі І-регулятора

. /5.20/

Аналіз /5.20/ показує, що критичний коефіцієнт передачі регулятора залежить від сталих часу і коефіцієнта передачі об’єкта, при цьому із збільшенням величини параметрів критичне значення коефіцієнта зменшується.

Далі знайдемо вираз для критичного коефіцієнта передачі системи для випадку використання ПІ-регулятора з передаточною функцією

. /5.21/

У цьому разі передаточна функція розімкненої системи

/5.22/

Відповідно передаточна функція замкнутої системи з ПІ-регулятором

/5.23/

Характеристичне рівняння системи з ПІ-регулятором

. /5.24/

З умови знаходження системи на границі стійкості , знаходимо критичне значення коефіцієнта передачі інтегральної частини ПІ-регулятора при фіксованому значенні коефіцієнта передачі пропорційної частини

/5.25/