1. Прямое программирование.

Из передаточной функции запишем линейное уравнение регулятора:

Выразим обратное z- преобразование к обеим частям уравнения:

Применяя метод прямой (непосредственной) декомпозиции к предыдущему уравнению

,

где или ,

получим систему:

Структура решения данной системы уравнений приведена на рис.7.8.

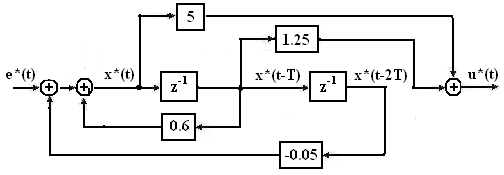
Рис.7.8 Прямое программирование передаточной функции

2. Последовательное программирование.

Передаточную функцию регулятора запишем в виде произведения двух функций, например, вида:

Программирование выполним, представив произведение передаточных функций системой уравнений:

X(z)=(1+0.25z^-1)E(z)+0.5z^-1X(z)

U(z)=5X(z)+0.1z^-1U(z).

Структурная схема решения системы приведена на рис.7.9.

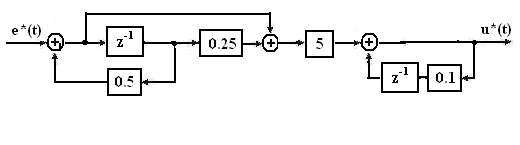
Рис.7.9 Последовательное программирование передаточной функции

3. Параллельное программирование.

Разложим передаточную функцию регулятора на сумму простейших:

Составим систему уравнений, U(z)=U₁(z)-U₂(z)

U₁(z)=9.375E(z)+0.5z^-1U₁(z)

U₂(z)= 4.375E(z)+0.1z^-1U₂(z),

структурная схема решения системы приведена на рис.7.10.

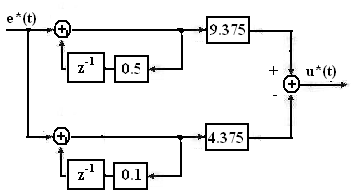
Рис.7.10 Параллельное программирование передаточной функции

Для преобразования сложной дискретной передаточной функции к алгебраической сумме элементарных используйте две леммы высшей

алгебры:

Лемма 1. Пусть - правильная рациональная дробь с действительными коэффициентами и пусть S₁ есть вещественный корень полинома Q(s)

кратности r, тогда существует такое число А и такой полином P₁(s), что

справедливо равенство

,

где ; при этом - правильная рациональная дробь.

Лемма 2. Пусть - правильная рациональная дробь с действительными коэффициентами и Q(s)=(s²+ps+q)^m∙V(s), где , корни полинома не

являются корнями полинома V(s), V(s) не делится нацело на (s²+ps+q).

Тогда найдутся такие вещественные числа M и N и такой полином P₁(s),что

,

где второе слагаемое будет также правильная рациональная дробь.

Пример:

Здесь использован метод неопределённых коэффициентов:

Варианты заданий приведены в таблице:

Номера вариантов	Дискретные передаточные функции регуляторов	kp	kd	ki	T,c
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17		1,45 1,5 1,4 2 3,2 2,2 1,3 3 1 1,6 1,55 2,1 2,3 3,8 1,65 1,47 1,49	0,43 0,48 0,42 1,5 0,4 1,2 0,38 2,2 0,44 1,1 0,52 0,45 1.43 0,39 0,47 0,54 0,62	1 1,3 1,2 0,8 0,5 1,5 0,9 1,1 1,4 0,7 0,6 0,85 0,95 0,93 0,77 1,06 1,12	0,1 0,12 0,11 0,09 0,05 0,04 0,08 0,07 0,02 0,14 0,095 0,03 0,06 0,065 0,13 0,097 0,032
18
19
20

Примечание:

1. .