Алгоритм исследования устойчивости замкнутой сау:

• определяем передаточную функцию замкнутой системы

где W_пк(p) – передаточная функция прямого канала системы; W_ос(p) – передаточная функция обратной связи;

• записываем характеристическое уравнение замкнутой системы:

(Т₁р+1)(Т₂р+1)(Т₃р+1)+k₁k₂k₃=0;

после преобразования этого выражения получим:

Т₁Т₂Т₃р³+(Т₁Т₂+Т₁Т₃+Т₂Т₃)р²+(Т₁+Т₂+Т₃)р+(1+k₁k₂k₃)=0;

обозначим:

а₀=T₁T₂T₃;

a₁=Т₁Т₂+Т₁Т₃+Т₂Т₃;

а₂=Т₁+Т₂+Т₃;

а₃=1+k₁k₂k₃;

тогда выражение примет стандартную форму:

а₀р³+а₁р²+а₂р+а₃=0;

• условия устойчивости замкнутой системы 3-го порядка:

1. а₀>0, a₁>0, a₂>0, a₃>0 (условие Рауса);

2. a₁a₂>a₀a₃ (условие Гурвица);

если условия устойчивости имеют место, то система устойчива;

• система на границе устойчивости, если выполняется равенство в условии Гурвица, отсюда определяется критическая величина передаточного коэффициента разомкнутой системы:

;

• заключение об устойчивости системы.

Приложение 4

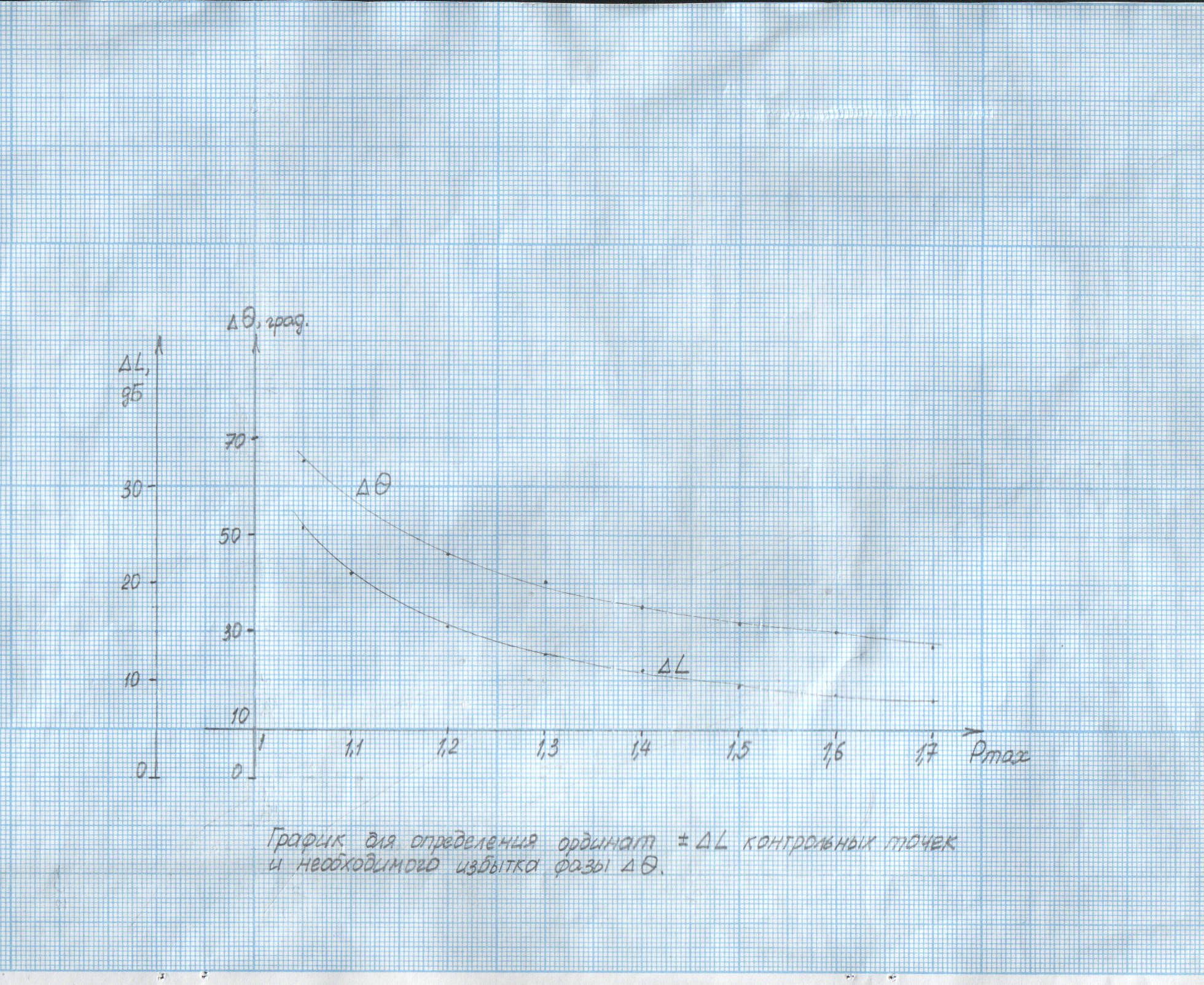
Приложение 5

Пример

Передаточная функция аналогового корректирующего устройства имеет вид

.

Определите дискретную передаточную функцию цифрового алгоритма управления объектом путём преобразования аналогового регулятора в цифровой при периоде квантования сигналов T=0,02с. Проверьте адекватность преобразования по амплитудно-фазовым частотным характеристикам непрерывного и цифрового корректирующих звеньев. Составьте программу работы ЦВМ на основании полученной дискретной передаточной функции и постройте структурную схему реализации алгоритма дискретного корректора.

Решение

Для получения дискретного аналога корректирующего алгоритма в форме обратных разностей используем аппроксимационную формулу Тастина

,

приведём первый коэффициент знаменателя к 1 и разделим числитель и знаменатель дискретной передаточной функции на :

.

Из последнего выражения

,

.

Обратное Z-преобразование этого выражения – рекуррентная форма дискретного управляющего алгоритма:

.

Структурная схема реализации полученного алгоритма в микроЭВМ представлена на рис.1.

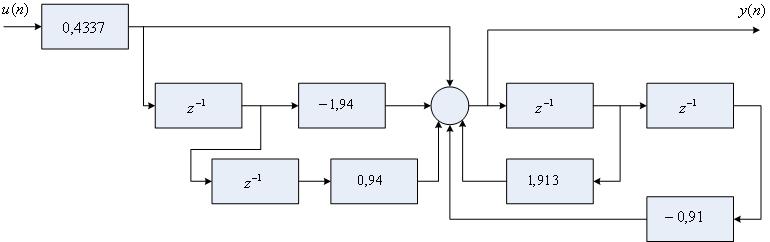
Рис.1. Структурная схема дискретного управляющего алгоритма

syms p syms t syms p

f=1/(p+1); f=t^3; f=1/p;

ilaplace(f) laplace(f) ed=ilaplace(f)

ans= ans= ed=1

exp(-t) 6/p⁴

syms p alpha syms t

f=1/(alpha + p); diff(heaviside(t),t)

ilaplace(f) laplace(ans)

1/exp(alpha*t) 1

ilaplace(ans)

dirac(t)

num=[6.66 1];

den=[66.6 1];

Wp=tf(num,den)

Ts=0.001;

Wz=c2d(Wp,Ts)

Transfer function:

6.66 s + 1

----------

66.6 s + 1

Transfer function:

0.1 z - 0.09998

---------------

z - 1

Sampling time: 0.001