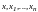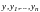3.3.5. Блок люфта.

В пакете Simulink нелинейность «насыщение» представлена блокомDiscontinuities/Backlash.

Назначение:

Моделирует нелинейность типа “люфт”.

Параметры:

Deaband width – Ширина люфта.

Initial output – Начальное значение выходного сигнала.

Сигнал на выходе будет равен заданному значению Initial output, пока входной сигнал при возрастании не достигнет значения (Deaband width)/2 (где U – входной сигнал), после чего выходной сигнал будет равен U-(Deaband width)/2. После того как, произойдет смена направления изменения входного сигнала, он будет оставаться неизменным, пока входной сигнал не изменится на величину (Deaband width)/2, после чего выходной сигнал будет равен U+(Deaband width)/2.

На рис. 3.15 показан пример работы блока Backlash. Входной сигнал блока гармонический с линейно возрастающей амплитудой.

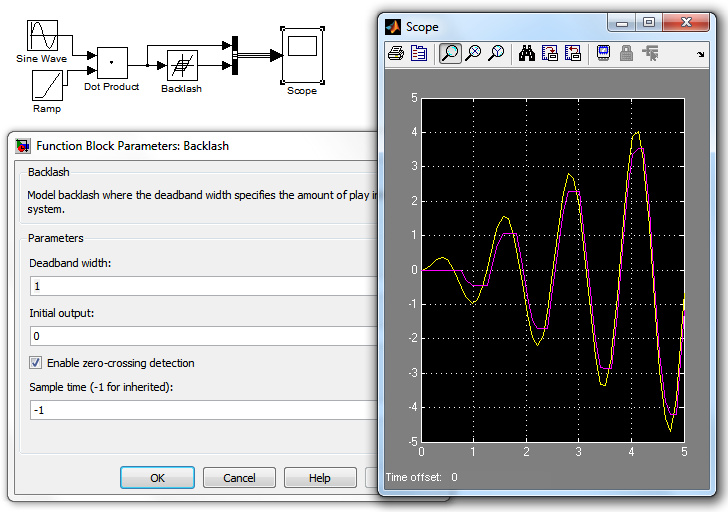
Рис.3.15. Пример работы нелинейности типа «Люфт».

3.4. Неаналитические нелинейности.

Неаналитические нелинейности - такие, что не могут быть описанные аналитическими выражениями, либо заданные таблицами и графиками.

К этой группе относятся нелинейности, обусловленные кривыми намагничивания, вольт-амперными характеристиками нелинейных сопротивлений и т.п.

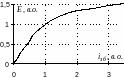
Рис.3.16. Нормированная кривая намагничивания

Типичным, широко распространенным примером такой нелинейности является кривая намагничивания (рис.3.16.). Начальный участок - это практически прямая линия, дальше – насыщающаяся кривая.

Существует два основных метода моделирования таких нелинейностей: интерполяция и аппроксимация.

3.4.1. Интерполяция нелинейностей.

Довольно часто на практике встречаются случаи, когда функция задана не аналитически, а в виде таблицы. В процессе моделирования нужно находить значения функции в точках, которые принадлежат интервалу задачи, но не совпадают с приведенными в таблице.

В этих случаях применяется особый прием построения приближенной функции, близкой к исходной, и определения аналитического выражения, которым можно воспользоваться для приближенных вычислений.

Рассмотрим основные подходы, которые применяются на практике. Пусть известные значения некоторой функции 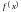образовывают такую таблицу 3.1.:

Таблица 3.1.

Значение функции

Классический подход к решению задачи нахождения приближенной функции основывается на требовании совпадения значений функции и приближенной функции 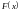в точках 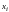( 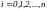), то есть выполнение равенств

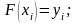
В этом случае процедуру нахождения приближенной функции называют интерполяцией, а точк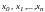и - узлами интерполяции.

Удобнее всего искать интерполирующую функцию в виде многочлена, поскольку его значение легко вычислить за конечным числом шагов, интегрировать, дифференцировать, используя лишь основные арифметические операции добавления, отнимание и умножение.

Перечислим основные методы построения интерполяционных полиномов:

• метод Лагранжа;

• разностная схема Ньютона;

• кусочная интерполяция кубическими полиномами;

• кубические многочлены Эрмита;

• кубические многочлены Бесселя;

• интерполяция кубическими сплайнами;

• интерполяция тригонометрическими полиномами.